1 . Момент количества движения материальной точки

Пусть материальная точка М массой m движется со скоростью V.

Кинетическим моментом относительно какого-либо центра О называют момент количества движения точки относительно этого центра.

Проведём полную аналогию момента силы относительно начала координат О и относительно оси z с моментом количества движения точки (различие лишь в направлении векторов).

(1)

- алгебраический момент силы относительно точки,

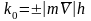- алгебраический момент количества движения относительно

того же центра.

Если точка совершает сложное движение, то 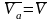, где .

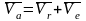Проецируя (1) на оси декартовой системы координат, получим выражения моментов количества движения (кинетические моменты) материальной точки относительно этих осей:

(1’)

,

,

.

алгебраические моменты силы и количества движения материальной точки относительно оси Z. координат(z).

,

.

2.Теорема об изменении момента количества движения материальной точки

Теорема выражает зависимость между моментом количества движения относительно точки и оси и моментом силы относительно тех же точки и оси.

Продифференцируем по t векторное равенство (1)

.

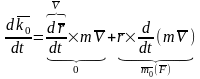Но , а 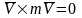,т.к. вектора направлены по одной прямой.

.

С

движения материальной точки.

ледовательно, (2)- теорема об изменении момента количества

Проецируя (2) на оси координат, получим:

(3)- та же теорема относительно

координатных осей.

Читать (2) и (3). При движении материальной точки производная по времени от момента ее количества движения относительно какого-либо центра (оси) равна моменту действующей на точку силы относительно того же центра (оси).

1. Теорема об изменении кинетического момента механической системы

Пусть движется система n материальных точек. На точки системы действуют внешние и внутренние силы.

Для каждой точки системы относительно некоторой точки О:

(4)

Просуммируем по всем точкам системы:

(5)

(6)

Обозначим - главный кинетический момент системы

относительно центра О.

- главный момент внешних сил относительно того

же центра О.

Таким образом, (6) примет вид:

(7)- теорема о кинетическом моменте системы.

Проецируя обе части (7) на неподвижные оси координат, получим:

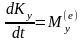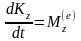; ; (8)- теорема об изменении кинетического

момента системы в координатной форме.

Читать (7) и (8). При движении механической системы производная по времени от главного кинетического момента относительно некоторого центра (оси) равна главному моменту всех внешних сил, действующих на эту систему относительно того же центра (оси).

Следствия (законы сохранения кинетического момента)

1. Если главный момент внешних сил относительно некоторого центра равен нулю, то главный кинетический момент системы относительно этого центра остается величиной постоянной:

, ,

.

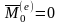2. Если главный момент внешних сил относительно некоторой оси равен нулю, то главный кинетический момент системы относительно этой оси остается неизменным:

, .