
- •Теорема об изменении количества движения
- •1.Теорема об изменении количества движения материальной точки
- •2.Теорема об изменении количества движения системы.
- •3.Законы сохранения количества движения
- •Дифференциальные уравнения поступательного движения твердого тела. Теорема о движении центра масс (центра инерции)
- •Следствия теоремы
- •Теорема об изменении момента количества движения (кинетического момента)
- •1 . Момент количества движения материальной точки
- •2.Теорема об изменении момента количества движения материальной точки
- •Теорема об изменении кинетического момента механической системы
- •4.Кинетический момент вращающегося тела
- •Дифференциальное уравнение вращательного движения
- •Дифференциальные уравнения плоского движения твердого тела
ЛЕКЦИЯ 13
Теорема об изменении количества движения
Теорема устанавливает зависимость между количеством движения материальной точки (системы) и импульсом действующей на точку (систему) силы.
Импульс силы - характеризует передачу материальному объекту механического движения за данный промежуток времени со стороны других действующих на него тел.
Действие
силы
 за
время
за
время
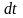 можно
охарактеризовать элементарным импульсом
силы
можно
охарактеризовать элементарным импульсом
силы

Полный импульс переменной силы, действующей в течение некоторого времени, выражается определенным векторным интегралом от вектора по скалярному аргументу t.

Проекции импульса силы на оси координат:

Модуль
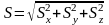 .
.
Направление
 В случае постоянной
по величине и направлению силы импульс
силы выражается вектором
В случае постоянной
по величине и направлению силы импульс
силы выражается вектором
 .
.
Направление этого вектора совпадает с направлением силы, а его модуль равен
 .
.
1.Теорема об изменении количества движения материальной точки
Пусть
точка М
массой m
движется под действием силы
 .
.
Запишем основное уравнение динамики: (1)
.
(2)
![]()
(1)- теорема об изменении количества движения материальной точки в дифференциальной форме;
(2)- другая форма той же теоремы, так называемая теорема импульсов в дифференциальной форме.
Читать (2). Дифференциал количества движения равен элементарному импульсу силы, действующей на эту точку.
Интегрируя (2) в пределах от 0 до t получим:
теорема
об изменении количества движения
материальной точки в интегральной
(конечной) форме.
 -(3)
-(3)

Геометрическая
интерпретация теоремы
Проецируя (2) и (3) на декартовы оси координат, получим:
 ,
,
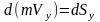 ,
(4)
,
(4)
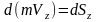 ,
,
теорема
об изменении количества движения
материальной
точки
в проекциях на оси координат.
 ,
,
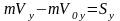 ,
,
 .
.
2.Теорема об изменении количества движения системы.
Пусть к точкам системы приложены как внешние так и внутренние силы. Тогда для каждой точки система (1) примет вид:
 (5)
(5)
Просуммируем по всем точкам системы:

∑ -
по свойству внутренних сил
-
по свойству внутренних сил
 -
главный вектор количества движения
системы.
-
главный вектор количества движения
системы.
Тогда
или
d
(7)![]()

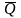 =∑d
=∑d
(6)- теорема об изменении количества движения системы в дифференциальной форме,
(7)- теорема импульсов в дифференциальной форме.
Читать (7). Дифференциал количества движения равен векторной сумме элементарных импульсов всех внешних сил, действующих на систему.
Интегрируя (7) от 0 до t получим:

 (8)
(8)
Читать. При движении механической системы изменение количества движения за некоторый промежуток времени равно векторной сумме импульсов всех внешних сил, действующих на систему за тот же промежуток времени (теорема о количестве движения системы в конечной форме).
Проецируя (7) и (8) на декартовы оси координат, получим:
теорема
о количестве движения системы в проекциях
на оси координат
(9)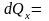
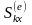 ,
,
 ∑
∑ ,
(9)
,
(9)
 ∑
∑
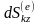 .
.
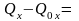 ∑
∑
 ∑
∑
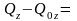 ∑
∑ .
.
