Кинетическая энергия твердого тела при поступательном и вращательном движениях

1. Поступательное движение

При поступательном движении

где V- скорость любой точки;

m-масса тела.

При поступательном движении тело можно считать материальной точкой.

2. Вращение твердого тела вокруг неподвижной оси

При вращательном движении

Обозначим

- момент инерции твердого тела относительно оси вращения.

Тогда

Читать: Кинетическая энергия твердого тела при вращении вокруг неподвижной оси равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости тела.

Замечание: М-масса - мера инерции тела при поступательном движении; J - момент инерции - мера инерции вращающегося тела.

Определение моментов инерции простейших однородных тел

1. Тонкий прямолинейный стержень - тонкий, если его толщиной по сравнению с длиной можно пренебречь.

(1)

Из условия однородности стержня

. (2)

Подставим (2) в (1) и проинтегрируем:

2. Круглое тонкое кольцо - тонкое, если по сравнению с радиусом толщиной можно пренебречь.

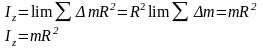
Радиус инерции

Для точек вращающегося твердого тела

Для точки.

Формула (1) определяет момент инерции любого тела, если известен его радиус инерции.

Радиус инерции ρ определяет расстояние от оси вращения до точки, в которой нужно сосредоточить всю массу тела, чтобы момент инерции точки относительно этой оси равнялся моменту инерции тела.

3. Круглый тонкий диск

(1)

И з условия однородности

(2)

Подставим (2) в (1) и проинтегрируем:

4. Сплошной цилиндр

Центр масс системы (центр тяжести твердого тела и его координаты)

Р ассмотрим систему n материальных точек. Положение каждой точки относительно системы отсчета Oxyz определяется в каждый момент времени радиус-вектором

или координатами .

Центром масс системы называется геометрическая точка С, радиус-вектор ,который определяется по формуле:

(1) - масса системы.

Положение центра масс не зависит от приложенных сил, а зависит от положения точек системы и их масс.

Проецируя обе части (1) на оси координат x,y,z получаем формулы, позволяющие определить координаты центра масс системы:

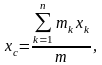
Умножим и поделим правые части (1) и (2) на g :

, ,…,… (3)

В (1) и (2):

- статический момент массы системы относительно полюса О,

, , - статические моменты масс системы относительно плоскостей zoy,xoz,xoy.

Если начало отсчета О совпадает с центром масс, то все статические моменты равны 0.

(1) 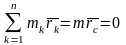, т.к. .

Если система находится в поле земного тяготения, то центр масс совпадает с центром тяжести.

Центр масс существует и в том случае, когда система находится за пределами поля земного тяготения