ЛЕКЦИЯ 12
Работа и мощность силы
Работа силы - мера механического воздействия, на материальную частицу со стороны других материальных объектов на данном ее пути, характеризующая переход немеханического движения в механическое и наоборот.
1. Работа постоянной силы при прямолинейном перемещении
Предположим,
что точка M
приложения постоянной силы
(постоянна
по величине и направлению) перемещается
из положения А
в В по прямолинейной траектории.
Вектор
силы
составляет с вектором перемещения
угол α.
(1)
при
α=0,
,
при
S
(α=
).
2. Элементарная работа силы
В общем случае, если сила переменна или движение точки приложения силы криволинейное, определить работу по (1) нельзя.
Пусть
точка приложения переменной по величине
и направлению силы F
описывает
криволинейную траекторию. Разобьем
весь путь на такие маленькие участки,
которые можно считать прямолинейными
и на которых можно пренебречь изменением
модуля и направления силы. Определим
на каждом участке элементарную работу.
(2);α-
угол,
который составляет сила с направлением
элементарного перемещения (которое
считается направленным по скорости
точки).
Если разложить силу на составляющие, то
(
)
т.к
(
dS).
Вывод: работу совершает только касательная составляющая силы.
3. Аналитическое выражение элементарной работы силы
Из
кинематики
(2)
примет вид:
,
т.е.
(3)
-
проекции силы на оси координат;
-
проекции вектора d
на оси координат.
Замечание: хотя выражение (3) по форме и напоминает полный дифференциал функции координат точки, в действительности в общем случае элементарная работа не является полным дифференциалом функции (исключение - потенциальные силы)
Поэтому обозначим d’
4. Полная работа силы на конечном перемещении
Рисунок тот же.
Разбив перемещение на участке АВ на элементарные, можно подсчитать полную работу силы.
,
Читать: полная работа силы на данном пути выражается криволинейным интегралом по дуге АВ от скалярного произведения вектора силы на вектор элементарного перемещения.
(
)
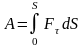
5. Мощность силы
Мощностью называют работу, совершаемую силой, в единицу времени.
Аналитическое
выражение
.
Определение работы в частных случаях
1. Работа силы тяжести
Силу тяжести материальной точки вблизи поверхности земли можно считать постоянной (по величине и направлению) и направленной вертикально вниз.
Если
спроецировать силу
на декартовы оси координат (см. рис), то
получим:
.
Вычисляя работу силы на перемещении от точки А до точки В, получим:
О
(1)
бозначив
запишем
Работа сила тяжести равна произведению этой силы на высоту подъема или опускания тела. «+» - опускание.
Из (1) следует, что работа силы тяжести не зависит от формы траектории, а в случае замкнутого контура =0.
В случае системы материальных точек работа силы тяжести равна произведению силы тяжести на разность высот конечного и начального положений центра масс системы.