
- •Индукция и дедукция как методы мышления. Полная и неполная индукции.
- •2. Метод математической индукции.
- •3. Применение метода математической индукции в различных разделах математики.
- •Числовые неравенства. Свойства числовых неравенств.
- •Методы доказательства неравенств.
- •Метод оценки знака разности левой и правой частей неравенства.
- •Доказательство неравенств на основании опорных неравенств.
- •3. Доказательство неравенств методом от противного.
- •4. Доказательство неравенств методом математической индукции.
- •Доказательство неравенств методом полной индукции.
- •6. Доказательство неравенств с помощью методов математического анализа.
- •Иррациональные уравнения.
- •Иррациональные неравенства.
- •Текстовые задачи
- •1. Применение графиков функций при решении задач школьной математики
- •1. Применение графиков функций при решении задач школьной математики
- •1.1. Задачи на смеси и растворы
- •1.2. Задачи на движение
- •1.3. Задачи на совместную работу
- •2. Нестандартные текстовые задачи
- •2.1. Задачи, которые решаются при помощи неравенств
- •2.2. Задачи с целочисленными неизвестными
- •2.3. Задачи с альтернативным условием
- •2.4. Задачи, где число неизвестных превышает число уравнений
- •Литература
- •Показательные и логарифмические уравнения и неравенства
- •1. Показательные уравнения, основные методы их решения.
- •1. Метод уравнивания показателей.
- •2. Метод введения новых переменных.
- •Функционально-графический метод.
- •2. Показательные неравенства.
- •3. Логарифмические уравнения. Основные методы их решения.
- •4. Логарифмические неравенства.
- •Графики функций и уравнений
- •1.2. Преобразования, изменяющие масштаб
- •2. Построение графиков функций, выражение которых содержит знак модуля
- •3. Построение графиков суммы, разности, произведения и частного функций
- •3.1. Построений графиков суммы и разности функций
- •3.2. Построений графиков произведения и частного функций
- •4. Построение графиков сложных функций
- •5. Применение графиков функций при решении задач школьной математики Задачи с параметрами
- •Функциональный подход к решению уравнений, неравенств и их систем
- •1. Функциональный подход в новых тенденциях школьного математического образования.
- •2. Теоретическое обоснование методов функционального подхода.
- •Доказательство.
- •Доказательство.
- •3.Система задач на применение функционального подхода к решению уравнений и неравенств Решение уравнений, основанные на ограниченности функций
- •Решения уравнений, основанные на симметричности и четности функций
- •Литература
- •Понятие уравнения с параметром.
- •Аналитическое решение уравнения с параметром.
- •Графические приёмы решения задач с параметрами.
- •4. Функционально-графический подход.
- •Решение неравенств с параметрами.
- •Литература
Иррациональные неравенства.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т.д.
Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению:
Неравенство вида
 равносильно системе
равносильно системе
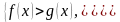
Неравенство вида
 равносильно неравенству
равносильно неравенству
 .
.Неравенство вида
 равносильно совокупности систем
равносильно совокупности систем

Неравенство вида
 равносильно системе
равносильно системе

Пример 5. Решим
неравенство
 .
.
Решение.
Введём новую переменную
 .
Тогда исходное неравенство принимает
вид:
.
Тогда исходное неравенство принимает
вид:
 .
.
Решая это неравенство
и возвращаясь к исходным переменным,
получаем:
 .
.
Ответ:
 .
.
Пример 6. Решим
неравенство
 .
.
Решение: Перепишем
неравенство в виде:
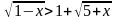 .
.
Это неравенство равносильно системе неравенств:
 Откуда
получаем
Откуда
получаем
 .
.
Пример 6. Решим
неравенство
 .
.
Решение:
Рассмотрим
функцию
 .
Область определения этой функции
.
Область определения этой функции
 .
Функция
возрастает на всей области определения,
причём
.
Функция
возрастает на всей области определения,
причём
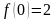 .
Значит, неравенство
.
Значит, неравенство
 решений не имеет.
решений не имеет.
Ответ: нет решений.
Литература
В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999
2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Текстовые задачи
План
1. Применение графиков функций при решении задач школьной математики
1.1. Задачи на смеси и растворы
1.2. Задачи на движение
1.3. Задачи на совместную работу
2. Нестандартные текстовые задачи
2.1. Задачи, которые решаются при помощи неравенств
2.2. Задачи с целочисленными неизвестными
2.3. Задачи с альтернативным условием
2.4. Задачи, где число неизвестных превышает число уравнений
1. Применение графиков функций при решении задач школьной математики
1.1. Задачи на смеси и растворы
Пусть смешивают
m1
кг раствора, содержащего x1%
контрольного вещества и m2
кг раствора, содержащего x2%
контрольного вещества. В результате
получают M = m1 + m2 кг
нового раствора, который содержит
0,01(m1x1 + m2x2) кг
контрольного вещества и имеет его
процентное содержание
 (1)
(1)
Это — формула взвешенного среднего величин x1 и x2, и она является рабочей для многих задач, в том числе для элементарных, базисных задач на определение итоговой концентрации (в %), исходной концентрации (количества) одного из смешиваемых веществ и т. д.
Простой анализ формулы (1) показывает, что величина x не зависит от абсолютных значений масс m1 и m2, а зависит только от их отношения, т. е. является однородной функцией от m1 и m2 порядка k = 0.
Что касается зависимости величины x от величин x1 и x2, то она носит линейный характер (важный частный случай однородности порядка k = 1). Тем самым, эта формула позволяет продемонстрировать еще одно важное понятие – понятие однородности выражения по переменным, которое будет востребовано в дальнейшем при решении тригонометрических, показательных и иных однородных уравнений.
Далее, формула (1) содержит два различных типа величин: экстенсивные количества и интенсивные процентные содержания. В самом деле, если мы прибавим к некоторому количеству m1 раствора с концентрацией x1 точно такое же количество m2 = m1 с концентрацией x2 = x1, то получим итоговое количество m = 2m1 , но с концентрацией x = x1.
Выясним, в чем
заключается графическая интерпретация
формулы (1). Рассмотрим числовую ось Ox,
на которой будем
отмечать составы смеси точками в
промежутке от 0 до 100, либо в относительных
единицах от 0 до 1. Припишем каждой точке
соответствующую массу. Тогда выражение
(1) задает хорошо известное из статики
положение центра масс (точки баланса)
системы двух материальных точек с
массами m1
и m2.
Положение центра масс легко находится
графически: путем деления отрезка [x1;
x2]
в отношении обратных масс
 (рис.1) .
(рис.1) .
Такое деление отрезка осуществляется элементарно через построение на нем двух подобных, для простоты, прямоугольных треугольников с вертикальными катетами, с длинами соответственно m2 и m1, но по разные стороны от этого отрезка. Это хорошо известное из статики «правило рычага», оно же «золотое правило механики»: чем больше вес (вообще сила), тем меньше должно быть ее плечо относительно точки баланса, и наоборот.
Этапы построения:
Отмечаем на оси Ox составы смесей x1 и x2 .
Откладываем от них m2 и m1 соответственно, по разные стороны от оси и перпендикулярно ей.
Соединяем концы катетов.
Точка пересечения с осью Ox – искомая средняя концентрация.

Рис. 1
Для
облегчения построения можно применить
другой прием, который допускает его
легкое последовательное использование
в задачах с числом исходных смесей n
> 2. А именно, катеты с длинами m1
и m2
откладываются от своих «родных» точек
числовой оси –
x1
и x2;
концы катетов соединяются отрезком, а
точка пересечения с осью симметрично
отражается относительно середины
отрезка

При решении задач с n 3 «массы» mi можно откладывать сразу вверх и вниз, а соединяющие линии проводить на выбор одним из двух описанных выше способов.
Cвойства cреднего взвешенного
На значения интенсивной величины x, найденной по формуле (1) распространяются все свойства, имеющие место для координаты центра системы точечных масс. А именно:
1) x (x1; x2) (x1 < x2);
2) при изменении x1 и x2 на одну и ту же величину , состав x изменяется на такую же величину;
3) при изменении x1 и x2 в одинаковое число раз величина x изменяется в то же число раз;
4) при изменении m1 и m2 в одинаковое число раз величина x не изменяется;
5) взвешенное среднее нуля и единицы равно весу единицы.
Заметим, что формула (1) обобщается на любое число n (n > 2) смешиваемых растворов с концентрациями xi, i =1, 2, …, n:
 (2)
Также сохраняются все вышеперечисленные
свойства с поправкой на число растворов.
(2)
Также сохраняются все вышеперечисленные
свойства с поправкой на число растворов.
Пример 1. Смешали 1,5 литра раствора соляной кислоты (HCl) с концентрацией 21,5% и 3,5 л с концентрацией 41,5%. Какова концентрация HCl в получившейся смеси?
Решение.
Если вычесть из концентраций величину = 21,5%, то получим растворы с концентрациями 0% и 20% соответственно.
«Центр масс» такой
смеси находится путем деления отрезка
длиной 20 в отношении 3,5:1,5 или же 7:3
(рис.2). Получим 14%.
Рис. 2
Теперь осуществляем обратный сдвиг на = 21,5% и получаем ответ 35,5% HCl.
Ответ: 35,5% .
Пример 2. Какой процентный состав получится при смешении m1 = 3,7 л водного раствора уксуса с концентрацией x1 = 34,5% с m3 = 3,7 литрами концентрации x3 = 54,5% и некоторого количества m2 раствора 44,5%–ной концентрации?
Решение.
Здесь мы имеем три (n = 3) исходные смеси. При этом применить рабочую формулу мы не можем, но не по причине неудобных данных, а ввиду отсутствия информации о количестве m2. Однако нетрудно видеть, что необходимости в задании этого количества нет. В самом деле, элементарное построение на оси Ox (рис. 6.3) делает наглядным и легко замечаемым симметричное расположение точек состава относительно x2 = 44,5%. Крайние «массы» (в данном случае объемы) m1 и m3 при этом отображаются отрезками одинаковой высоты. Следовательно, какой бы ни была масса m2, даже отрицательной в случае выпаривания такого раствора из смеси, концентрация получившегося раствора будет точно равна x2.


Рис. 3
Ответ: 44,5%.
В несколько усложненном варианте аналогичную задачу можно сформулировать для случая четырех (n = 4) исходных смесей, три из которых образуют симметрическое расположение. При этом также путем параллельного переноса все концентрации можно сделать неудобными для прямых вычислений.
Пример 3. Имеются два сплава, в одном из которых содержится 40 %, а в другом – 20 % серебра. Сколько килограмм второго сплава необходимо добавить к 14 кг первого, чтобы получить сплав с 34 %–ной концентрацией серебра?
Решение.
Откладываем на оси Ox заданные исходные концентрации 20% и 40% и конечную концентрацию 34%. От концентрации 20% откладываем катет, соответствующий 14 килограммам. Проводим прямую через конец этого катета и точку на оси Ox, обозначающую конечную концентрацию 34% до пересечения с перпендикуляром, отложенным от второй исходной концентрации 40%. Полученная длина катета соответствует 6 килограммам (рис. 4).

Рис. 4
Ответ: 6 кг.
