3. Доказательство неравенств методом от противного.

Для доказательства неравенства методом от противного предполагают, что верно противоположное неравенство. Преобразования этого неравенства приводят к противоречию с известными фактами, что даёт основание для утверждения справедливости исходного неравенства.

П р и м е р. Доказать неравенство , если

Доказательство. Предположим, что верно противоположное неравенство:

.

Возведём в квадрат, получим:

,

или

,

что равносильно неравенству

Получили противоречие. Значит если

4. Доказательство неравенств методом математической индукции.

Доказательство методом математической индукции основано на следующей аксиоме: если предложение, в формулировку которого входит натуральное число п, истинно при п=1 и из его истинности при n=k ( где ) следует, что оно истинно и при , то оно истинно при всех натуральных значениях п.

Таким образом, доказательство по методу математической индукции проводится следующим образом:

1. доказываемое утверждение проверяется при п =1;

2. предполагая справедливость утверждения при n=k, доказывается справедливость утверждения для n=k+1.

Некоторые утверждения справедливы не для всех натуральных п, а для п, начиная с некоторого числа р. В таком случае первый шаг доказательства – это проверка справедливости утверждения для п=р .

П р и м е р. Доказать, что если 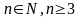, то

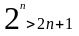
Доказательство. При n=3 неравенство верно: . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что

В самом деле, имеем: . Итак, .

Но 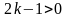при любом натуральном значении k. Следовательно, тем более .

Согласно методу математической индукции можно сделать вывод о том, что доказываемое неравенство справедливо при всех .

5. Доказательство неравенств методом полной индукции.

Полная индукция – это метод рассуждений, при котором вывод делается на основании рассмотрения всех случаев, возможных по условию задачи.

П р и м е р. Доказать, что если .

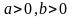Доказательство. Рассмотрим случаи:

1) . Получаем

, т.к.

Неравенство верно.

2) , т.е. .

Тогда . Неравенство справедливо.

3) т.е. .

Тогда . Неравенство справедливо.

Мы рассмотрели все возможные случаи. Значит неравенство верно для .

6. Доказательство неравенств с помощью методов математического анализа.

В этом случае доказательство неравенств сводят к исследованию соответствующих функций с помощью производных.

П р и м е р. Доказать неравенство

Доказательство. Перепишем неравенство в виде: .

Рассмотрим функцию .

Найдём производную . При , . Это значит, что при возрастает, причём . Поэтому при .

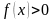Литература

1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999

2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000

Тема: Иррациональные уравнения и неравенства.

План

1. Иррациональные уравнения, основные методы их решения.

2. Иррациональные неравенства.