Решения уравнений, основанные на симметричности и четности функций

Пример 1. Решить уравнение . (4)

Решение. Внешний вид уравнения подсказывает, что одним из корней является число х₁ = . Воспользуемся тем, что

х²-х+1= .

Перепишем уравнение (4) в виде

.

Тогда видно, что х₂=1- х₁=1- - корень исходного уравнения, поскольку .

Покажем, что если х₁ (х₁0, х₁1) является корнем уравнения (4), то х₃= также есть корень этого уравнения. Это действительно так, потому что

.

Таким образом, если х₁ (х₁0, х₁1) – корень уравнения (4), то корнями уравнения также являются , 1-х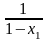_1, , 1- , , т. е. уравнение (4) имеет корни х₁= , х₂=1- , х₃= , х₄= , х₅=1- , х₆= . Так как исходное уравнение есть алгебраическое уравнение шестой степени, то оно имеет не более шести корней. Следовательно, найдены все корни уравнения (4).

Ответ: .

Пример 2. При каких значениях параметра а уравнение

x²-2asin(cosx)+2=0 (5) имеет единственное решение?

Решение. Так как у = х² и у = соs х - четные функции, то если существует некоторое х₀ — решение исходного уравнения, то (-х₀) - также является его решением. Значит, условие х₀=-х, откуда х₀=0, является необходимым условием существования у исходного уравнения единственного корня. Так как х₀=0 является решением, то, подставляя это значение в (5), получим

-2asin(1)+2=0  a= .

Осталось убедиться, что при этом значении а исходное уравнение действительно имеет лишь один корень. Запишем (5) в виде

x²- sin(cosx)+2=0  (x²+2) sin1=2sin(cosx).

Заметим, что (x²+2)sin1≥2sin1, а 2sin(cosx)≤ 2sin1, следовательно, х = 0 является единственным корнем уравнения при данном значении параметра.

Ответ: a= .

Пример З. При каких значениях параметра а уравнение (6) имеет нечетное число корней?

Решение. Рассмотрим функцию f(х)= . Так как

f(-x)= f(x),

то f(x) является четной функцией. Следовательно, если некоторое значение переменной х₀ является корнем уравнения (6), то (-х₀) - также его корень. Следовательно, если уравнение (6) имеет решения, то имеет четное число корней, кроме случая, когда х=0 является одним из корней, т. е. выполняется равенство│2а│=а² + 1, откуда а =1. При каждом из этих значений параметра уравнение (6) действительно имеет по крайней мере корень х =0, поэтому проверять, есть ли еще решения и каковы они, нет необходимости.

Ответ: а=1.

Пример 4. При каких значениях параметра а система уравнений

(7)

имеет единственное решение, удовлетворяющее ограничению

х[-6; 0]?

Решение. Рассмотрим функцию f(у) = (3-2 )^y+(3+ )^y, стоящую в левой части первого уравнения системы (7).

Так как

(3+ )^y=(3+2 )^y= ,

то функция f(у) является четной. Следовательно, если некоторая пара (х_0;y₀) является решением исходной системы, то (х₀;-y₀) также является решением. Следовательно, для того чтобы система (7) имела единственное решение, необходимо, чтобы у₀ =0 . При этом условии система принимает вид

(8)

Из второго уравнения имеем х =0 при любом а либо хR при а² -5а+6=0 В первом случае первое уравнение в (8) примет вид 2-За=5, откуда

а=-1. Во втором случае а=2 или а=З. Если а = 2, то из первого уравнения находим х = -З , и это значение удовлетворяет условию х[-6; 0]. Если же а=3, то у первого уравнения нет решений.

Ответ: а = -1; а= 2.

Пример 5. При каких значениях параметра а система уравнений имеет четыре решения?

(9)

Решение. Преобразуем второе уравнение исходной системы, выделив полные квадраты (7у)² + (х-1)² + 4а = 0. Следовательно, функции в системе симметричны по переменной х относительно значения х =1 и четные по переменной у. Значит, если пара (х₀; у₀) - решение системы, то также решениями являются (х₀; -у₀), (2-х₀; у₀), (2-х₀; -у₀). Кроме того заметим, что если сделать замену переменных v = 7 и u = , то получим систему

(10)

которая является симметричной относительно u, v, т. е. вместе с любой парой (u; v), где u >0, v >0, решением является и пара (v; u). Следовательно, исходная система если имеет, то имеет не менее восьми решений, кроме трех случаев: 1) u= v, 2) u = 0, З) v =0. А тогда, если u= v, то а =- , в случае u = 0 имеем а =- , а если v =0, то а = - . Осталось проверить каждое из найденных значений а и удостовериться, что система (10) действительно имеет два решения, а значит, система (9) имеет четыре решения.

Ответ: а =- ,а =- .

Пример 6. При каких значениях параметра а система уравнений (11) имеет единственное решение?

Решение. Выделим в каждом из уравнений данной системы полные квадраты

(11) 

Теперь видно, что система (11) «симметрична» относительно х-1 и у+2 т. е. если сделать замену переменных u = х-1, v = у+2 и некоторая пара (u₀;v₀) является решением, то (v₀; u₀) - также решение. Следовательно, необходимым условием существования единственного решения у системы (11) является равенство u₀=v₀, откуда х = у + 3. Подставляя это выражение во второе уравнение (11), получаем

2ау²+ 8ау-у-3+10а+1=0  2ау²+ у(8а-1)+10а-2=0.

Это уравнение имеет единственное решение либо если оно является линейным (т. е. а =0), либо если оно квадратное и D=(8a-1)²-4*2a*(10a-2)=1- -16a²=0, т. е. при условии а = . Подставляя найденные значения параметра а в систему (11), убеждаемся, что при каждом из них она действительно имеет единственное решение.

Ответ: - ; 0; .

Пример 7. При каких значениях параметра а система (12) имеет единственное решение?

Решение. Первое и третье уравнения исходной системы являются симметричными относительно переменных х н у. Однако из внешнего вида второго уравнения в (12) такой вывод сделать нельзя. Выделим в нем полный квадрат относительно х

х²-2х+(у-1)²+z=a • (x-1)²+(y-1)²+z²=a+1.

Теперь видно, что если некоторая тройка (х₀; у₀; z₀) является решением системы (12), то и тройка (у₀; х₀; z₀) - также решение системы. Следовательно, решение будет единственным только тогда, если выполнено условие х₀ = у_0. Тогда исходная система примет вид

(13)

Из первого уравнения следует, что siп2х=0 , но это уравнение имеет бесконечно много решений. Однако ОДЗ переменной х системы определяется неравенством 1-х²>0, т. е. х  (-1; 1) , значит, в ОДЗ переменной лежит лишь решение х =0.

Итак, имеем условие х = у =0 и, подставляя в (13), получаем систему Относительно переменной z:

(14)

Если некоторое z₀ – решение системы (14), то (-z₀) – также решение. Следовательно, условие z=0 – еще одно необходимое условие существования единственного решения у системы (12), откуда получается а=1. При таком значении параметра исходная система приобретает вид

Преобразуем второе уравнение к виду х² + у² +z²-2х-2y=0 и подставим выражение х + у =-sin²z из третьего уравнения.

Тогда имеем уравнение

х² + у² +z²+2sin²z=0 • x=y=z=0.

То есть тройка (0; 0; 0) действительно является единственным решением системы (12) при а = 1.

Ответ: а =1.

Пример 8. При каких значениях параметра а системы уравнений (15) и (16) равносильны?

Решение. Система (15) является линейной. Она не имеет решений, если выполнены соотношения , т. е. при а=-2. Подставим это значение в (16). Имеем

Вычитая из второго уравнения первое, имеем

х²-7х+у⁴+у²+21=0 • •

•

Это уравнение и, следовательно, (16) не имеют решений. Итак, при

а=-2 обе системы не имеют решений, а значит, равносильны.

Пусть теперь а а-2. Тогда линейная система (15) имеет единственное решение при любом значении параметра. Значит, необходимым условием равносильности систем (15) и (16) является то, что система (16) имеет единственное решение. Но если пара (х₀; у₀) является решением (16), то пара (х₀;-у₀) тоже будет ее решением. Поэтому необходимым условием существования единственного решения является у₀ = -у откуда у₀ =0.

Подставляя у=0 в (16), получаем систему для нахождения х и а:

(17)

Из первого уравнения находим х₁ = 1 или х₂ =3 , тогда, подставляя эти значения во второе уравнение системы (17), находим а = 1 или а =3, и а =1.

Осталось проверить каждое из найденных значений.

При а = 1 значения х = 1, у = 0 являются решением (15), но у (16) есть еще одно решение - х = 3, у = 0, и эти значения не являются решением (15).

При а =3 значения х = 1, у = 0 не являются решением (15).

При а =-1 значения х = 3, у =0 являются решением (15), и т. к. второе уравнение в (16) примет вид у²=-2(х-3) то (16) тоже имеет единственное решение - х = 3, у = 0.

Ответ:а=-2; а =-1.