5. Применение графиков функций при решении задач школьной математики Задачи с параметрами

В зависимости от того, какая роль отводится параметру в задаче (неравноправная или равноправная с переменной), можно соответственно выделить два основных графических приема: первый – построение графического образа на координатной плоскости (x; y), второй – на (x; a).

Задача 5. Найти все значения параметра а, при которых уравнение имеет решение.

Решение.

Переходя к логарифмам по основанию 5, получаем уравнение , которое равносильно уравнению (1), если выполняется условие 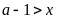(2). Выражая x из равенства (1) и подставляя в неравенство (2), получаем неравенство (3). Чтобы решить это неравенство, решим сначала уравнение .

Построим графики функций и (рис. 20). Тогда – есть решение этого уравнения. Так как мы решаем неравенство , видно, что график функции расположен выше графика функции на промежутке , тогда решение неравенства .

Рис. 16

Ответ: .

Задача 6. При каких значениях a система уравнений

не имеет решений?

Решение.

Система равносильна исходной.

На рис. 21 точка (3; 0) – центр поворота. Ясно, что если прямая семейства вращается внутри угла OMA, то система не имеет решений. Устанавливаем, что угловой коэффициент прямой MA равен . Тогда при таком повороте параметр a принимает все значения из промежутка (– ; 0]. Заметим, что мы включили a = 0, поскольку прямая MO не пересекает гиперболу.

Важно при записи ответа не упустить, что существует еще одна прямая семейства, а именно у = – х + 3, проходящая через «дырки» в гиперболе. Поэтому при а = –1 система также не имеет решений.

Рис. 17

Ответ: а = –1 или .

Задача 7. При каких значениях параметра а уравнение 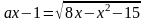имеет единственное решение?

Решение.

Рассмотрим функции у = ах и . График второй функции легко построить, рассмотрев уравнение (у – 1)² = 8х— х² — 15 при у ≥ 1. Преобразовав последнее к виду (у – 1)² + (х – 4)² = 1, получаем, что искомый график — полуокружность с центром (4 ; 1) и радиусом 1. На рис. 22 это дуга АВ. Все прямые у = ах, про­ходящие между лучами OA и ОВ пересекают дугу в одной точке. Также одну точку с ду­гой имеют прямая ОВ и касательная ОМ. Легко показать, что угловые коэффициенты прямых ОВ и OA соответствен­но равны и . Устанавливаем, что угловой коэффициент касательной ОМ равен 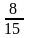, причем это можно сделать не обязательно при помощи производной. Действительно, потребо­вав от системы

иметь одно решение, получим а = .

Рис. 18

Итак, прямые семейства у = ах имеют с дугой АВ только одну общую точку при ≤ а < или а = .

Ответ: ≤ а < или а = .

Литература

1. Архипов Б.М., Мазаник А.А., Петровский Г.Н., Урбанович М.И. Элементарные функции – Мн: Вышэйшая школа, 1991.

2. Бахтина Т. П. «Таблетки» и «компрессы» при построении графиков. // Математика в школе. – 2004 – №8.

3. Гельфанд И.М., Глаголева Е.Г., Шноль Э.Э. Функции и графики. – М.:МЦНМО, 2001.

4. Ершов Л.В., Райхмист Р.Б. Построение графиков функций – М.: Просвещение, 1984.