3. Логарифмические уравнения. Основные методы их решения.

При решении логарифмических уравнений во многих случаях приходится использовать свойства логарифмов. Напомним их.

Определение. Логарифмом числаb по основанию а называется показатель степени, в которую надо возвести а, чтобы получить b.

,

Свойства логарифмов:

1. , где

2. , где

3. где

4. где

5. где

6. ,где

7. , где

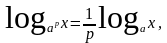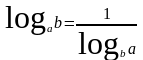8. , где

Заметим, что эти преобразования неравносильны. Применение этих формул в одну сторону приводит к расширению области определения, а в другую – к сужению.

Уравнение вида равносильно системе:

Уравнение вида 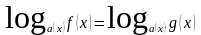равносильно системе:

С помощью тождественных преобразований более сложные логарифмические уравнения приводятся к простейшим. При решении также используются более общие методы решения уравнений: разложение на множители, введение новых переменных, функционально-графический.

Рассмотрим несколько примеров.

Пример 10. Решим уравнение

Решение. Выполняем последовательно преобразования:

Необходима проверка:

Ответ: .

Пример 11. Решим уравнение

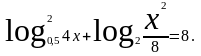
Решение. Переходим к новому основанию и выполняем последовательно преобразования:

Введём новую переменную:

Получаем уравнение: .

Откуда

Возвращаемся к подстановке, получаем:

Откуда

Ответ: .

4. Логарифмические неравенства.

Решение логарифмических неравенств вида

, где

Основано на следующих двух теоремах:

Теорема 1. Если то неравенство равносильно системе неравенств

Теорема 2. Если то неравенство равносильно системе неравенств

Пример 12. Решим неравенство

Решение. Это неравенство можно переписать так:

В соответствии с теоремой 2 получаем систему неравенств:

Эта система равносильна неравенству

Из которого получаем -- решение заданного неравенства.

При решении логарифмических неравенств используется также обобщённый метод интервалов.

Пример 13. Решим неравенство

Решение. Выполняем последовательно преобразования неравенства:

Для функции находим область определения и значения аргумента, при которых функция принимает значение ,равное нулю:

Отмечаем на координатной прямой, определяем знаки функции на полученных промежутках: .

Выбираем решение:

Литература:

1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М., 1999

2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000