2. Метод введения новых переменных.

Метод введения новых переменных позволяет свести показательное уравнение к алгебраическому уравнению относительно некоторой показательной функции.

Рассмотрим несколько примеров.

Пример 3. Решим уравнение

Решение.

Введём новую переменную: . Заметим, что .

Исходное уравнение принимает вид:

.

Это квадратное уравнение имеет два корня: .

Возвращаясь к своей подстановке, получаем:

1) ;

2)

Ответ:

Пример 3. Решим уравнение:

.

Решение.

Так как 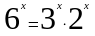, то имеем:

.

Так как ни при каких значениях x не обращается в нуль, то, разделив обе части полученного уравнения на 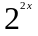, получаем равносильное уравнение:

.

Полагая , получаем квадратное уравнение: , откуда

Возвращаясь к своей подстановке, получаем:

1)

2)

Ответ:

4. Функционально-графический метод.

Этот метод основан на использовании графических иллюстраций и свойств функций, входящих в уравнение.

Рассмотрим несколько примеров.

Пример 4. Решим уравнение

Решение.

Разделим обе части уравнения на . Получим уравнение равносильное исходному уравнению:

.

Левая часть уравнения представляет собой убывающую функцию.

Поэтому, если уравнение имеет корень, то он единственный. Очевидно, что является корнем уравнения.

Ответ:

Пример 5. Решим уравнение

Решение.

Перепишем уравнение в виде:

.

Сравним области значений функций, стоящих в правой и левой частях уравнения.

Введём обозначения: и

,

.

Равенство возможно только в случае одновременного выполнения условий:

, то есть .

Очевидно, .

Ответ:

Пример 6. Решим уравнение

.

Решение. Преобразуем левую часть уравнения:

Отсюда получаем:

Первое уравнение совокупности корней не имеет. Второе уравнение переписываем в виде:

Так как не является корнем уравнения, то разделим обе части уравнения на x. Получаем:

.

Обозначим 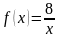и .

Уравнение принимает вид: . Функция -- убывающая, функция -- возрастающая. Если уравнение имеет корень, то он – единственный. Очевидно, что .

Ответ:

2. Показательные неравенства.

Решение показательных неравенств вида , где , основано на следующих теоремах:

Теорема 1. Если то неравенство равносильно неравенству .

Теорема 2. Если , то неравенство равносильно неравенству .

Рассмотрим несколько примеров.

Пример 7. Решим неравенство .

Решение. Так как , то данное неравенство равносильно неравенству

,

решением которого является интервал (-1;7)

Ответ: (-1;7)

Пример 8. Решим неравенство .

Решение.

Последовательно получаем:

Решаем полученное неравенство методом интервалов и получаем:

Пример 9. Решим неравенство

Решение.

Перепишем неравенство в виде .

Разделим обе части неравенства на . Так как , получаем

.

Обозначим и получаем неравенство , из которого имеем . Последовательно получаем:

Ответ: