Литература
3000 конкурсных задач по математике /Под ред. проф. Н.А.Бобылева. - М.: Рольф, 1997.
2. Азаров А.И., Барвенов С.А., Федосенко B.C. Текстовые задачи. - Мн.: Аверсэв, 2005.
3. Азаров А.И., Барвенов С.А., Федосенко B.C., Шибут А.С. Системы алгебраических уравнений. Текстовые задачи.- Мн.: ТетраСистемс, 1998.
4. Барабанов Е.А., Воронович И.И., Каскевич В.И., Мазаник С.А. Задачи районного тура Минской городской математической олимпиады школьников. – Мн., Фаритекс, 2002.
5. Бахтина Т. П. Готовимся к олимпиадам, турнирам и математическим боям. Математикон 8. - Мн.: Аверсэв, 2003.
6. Габринович В.А., Громак В.И. Решим любую задачу. Задачи на экзаменах по математике в БГУ в 1995 году с решениями и комментариями: учеб пособие. - Мн.: Белгосуниверситет, 1996.
7. Кипнис И.М. Задачи на составление уравнений и неравенств. - М.: Просвещение, 1980.
8. Лурье М.В. Задачи на составление уравнений. Техника решения. - М.: УНЦ ДО, 2004.
9. Лурье М.В., Александров Б.И. Задачи на составление уравнений. - М.: Наука, 1990.
10. Мельников И.И., Сергеев И.Н. Как решать задачи по математике на вступительных экзаменах. - М.: Изд-во Моск. ун-та, 1990.
11. Фарков А.В. Математические олимпиады в школе 5 – 11 классы. - М.: Айрис пресс, 2003.
Показательные и логарифмические уравнения и неравенства
План
Показательные уравнения, основные методы их решения.
Показательные неравенства.
Логарифмические уравнения, основные методы их решения.
Логарифмические неравенства.
1. Показательные уравнения, основные методы их решения.
Показательными уравнениями принято называть уравнения, в которых неизвестное входит только в показатели степеней при постоянных основаниях.
Простейшее показательное уравнение имеет вид:
,
где
При
данное уравнение не имеет решений;
При
его решением является
.
Если вместо х
в показателе степени стоит какая-нибудь
функция
,
то уравнение вида
,
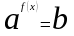где
,
приводят к равносильному уравнению
.
При решении показательных уравнений используются следующие методы:
Метод уравнивания показателей.
Метод введения новых переменных.
функционально-графический метод.
1. Метод уравнивания показателей.
Решение уравнений с помощью этого метода основано на следующей теореме:
Теорема: Показательное уравнение
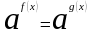(где
)
равносильно
уравнению
.
Пример 1. Решим уравнение
Решение.
Перепишем уравнение в виде
.
Полученное уравнение равносильно уравнению
.
Откуда
получаем:
.
Пример 2. Решим уравнение
.
Решение.
Перепишем уравнение в виде:
Разделив правую
и левую части уравнения на произведение
,
получаем:
или
.
Откуда
имеем
или
.