2.4. Задачи, где число неизвестных превышает число уравнений

При решении ряда текстовых задач их условия требуют введения оп­ределенного количества неизвестных. Попытка составить столько же уравнений, сколько и неизвестных, не приводит к успеху. Это проис­ходит по нескольким причинам. Иногда искомая величина представ­ляет собой комбинацию введенных неизвестных (такие ситуации встречаются в задачах на движение). В этих случаях вводятся новые неизвестные и задача ре­шается однозначно. В других задачах необходимо провести анализ полученных уравнений и тогда, если нужно, сделав соответствующие ограничения на неизвестные, также удается получить решение. Воз­можны, однако, и ситуации, при которых из меньшего количества уравнений удается найти большее количество неизвестных. Заметим, что задачи такого рода встречались и в рассмотренных ранее типах.

Задача 18. Три пункта А, В и С соединены прямолинейными доро­гами. К отрезку дороги АВ примыкает квадратное поле со сторо­ной, равной 0,5АВ; к дороге ВС примыкает квадратное поле со стороной, равной ВС; к дороге АС примыкает прямоугольный уча­сток леса длиной, равной АС, и шириной 4 км. Площадь леса на 20 км² больше суммы площадей квадратных полей. Найти площа­ди квадратных полей и площадь леса. [2, с.154]

Решение:

Пусть АВ = 2х, ВС = у, АС = z. Тогда из условия имеем равенст­во: х² +у² +20 = 42 <=>

<=> х² + у² +5 = z.

На первый взгляд может показаться, что все условия исчерпаны и пример неразрешим. Но ведь пря­молинейные дороги являются сторо­нами треугольника либо лежат на од­ной прямой.

Тогда z ≤ 2х+у <=> х² + у² +5 ≤ 2х + у. Отсюда, выделив полные квадраты, получим: .

Это возможно только тогда, когда одновременно выполняются равен­ства , откуда х = 4, у = 2. Тогда z = 10 и требуемые площади легко находятся. Кроме того, мы установили, что А, В и С на­ходятся на одной прямой.

Ответ: площадь леса 40 км², полей — 16 км² и 4 км².

Задача 19. Первый покупатель купил 14 м ткани первого вида, 5 м второго вида и 9 м третьего вида, за что вместе заплатил 160 евро. Второй приобрел соответственно 4, 13 и 9 метров таких тканей и заплатил за все 128 евро. Третий купил по 5 м ткани каждого вида. Сколько заплатил третий? Какая ткань дороже: первого или второго вида?

Решение: Обозначим стоимость тканей первого, второго и третьего вида через х у и z соответственно. Тогда из условия задачи составляем два уравнения с тремя неизвестными:

14х+5у+9z = 160,

4х + 13у+ 9z=128.

Сначала узнаем, сколько уплатил третий покупатель. По условию требуется найти величину 5х + 5у + 5z. Обычно в таких примерах тре­буемая величина находится из линейной комбинации составленных уравнений: необходимо умножить первое уравнение на некоторое чис­ло ά, второе — на β, а затем сложить или вычесть уравнения. Числа ά и β подбираются так, чтобы в результате сложения или вычитания полу­чилась искомая величина. В данном случае к требуемому приводит простое сложение уравнений. Имеем: 18(х + y + z) = 288, т.e. x + y + z =16. Следовательно, третий покупатель уплатил 5(х + у + z) = 5·16 = 80 евро. В примере нужно получить и второй ответ: что большее х или у? В таких случаях сначала из одного из уравнений исключается третье неизвестное. Вычтем из первого уравнения системы второе. Получим 10х - 8у= 32 <=> 5х — 4у = 16 . Из этого уравнения неясно, что больше: х или у. Однако из полученного соотношения х + у + z = 16 следует, что х < 16, у <16, z <16.

Тогда 5х -4у = 4(х - у)+ + у = 16. Так как у < 16, то, очевидно, выполняется 4(х – у) > 0, т. е. х > у.

Ответ: третий покупатель уплатил 80 евро; первая ткань дороже второй.

Задача 20. Имеется два различных сплава меди со свинцом. Если взять 1 кг первого сплава и 1 кг второго сплава и переплавить их, то получится сплав, содержащий 65 % меди. Известно, что если взять два некоторых куска — кусок А и кусок В первого и второго сплавов соответственно, имеющих суммарную массу 7 кг, и переплавить их, то получится сплав с содержанием 60 % меди. Какова масса меди, содержащейся в сплаве, получающемся при совмест­ной переплавке куска первого сплава, равного по массе куску В, и куска второго сплава, равного по массе куску А. [2, с.155]

Решение: Пусть концентрация меди в первом и втором сплавах равна соответст­венно х и у. Тогда, если сплавить по одному килограмму обоих сплавов, то получим сплав, в котором концентрация меди равна . Возьмем кусок А первого сплава. В нем содержится хА меди. В куске В второго сплава содержится уВ меди. Так как общая масса ново­го сплава равна А + В = 7 и в нем содержится (хА + у В) кг меди, то ее концентрация в сплаве будет , т. е. (хА + уВ) = 4,2. В куске В пер­вого сплава содержится х В меди, а в куске А второго сплава меди будет уА. Требуется узнать, чему равна масса меди в новом сплаве, т. е. чему равна величина (хВ+ уА). Использовав все условия задачи, удалось со­ставить только три уравнения с четырьмя неизвестными:

х + у = 1,3,

А + В = 7,

хА + уВ = 4,2

Однако и найти требуется не все неизвестные, а величину (хВ + уА). Перемножим левые и правые части первого и второго уравнений систе­мы. Имеем: (х + у)(А + В) = 9, 1 <=> (хА + у В) + (хВ + у А) = 9,1

Учитывая третье уравнение, получаем хВ + уА = 9,1 - 4,2 = 4,9 кг.

Ответ: масса меди 4,9 кг.

Задача 21. Резервуар наполняется водой по пяти трубам. Пер­вая труба наполняет резервуар за 40 мин; вторая, третья и чет­вертая, работая одновременно, — за 10 мин; вторая, третья и пятая — за 20 мин и, наконец, пятая и четвертая — за 30 мин. За какое время наполнят резервуар все пять труб при одновремен­ной работе? [2, c.157]

Решение: Пусть первая, вторая и т. д. трубы наполняют (каждая в отдельности) резервуар за х₁, х₂, х₃, х₄, х₅ мин (индекс у неизвестных соответствует номеру трубы). Тогда за одну минуту они заполнят соответственно часть резервуара. Из условия задачи можно составить следующую систему уравнений:

Фактически необходимо, найти выражение m = . Тогда искомое время будет равно . Умножим первое уравнение на второе, а затем сложим все уравнения. Получим

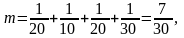т. е. т = . Таким образом, все пять труб заполнят резервуар, работая вместе, за часа.

Ответ: за часа.

Задача 22. Имеется два сплава с различным содержанием меди. Масса первого сплава т кг, масса второго сплава п кг. От каждого из сплавов отделили по одинаковому куску равной массы и каж­дую из этих частей сплавили с остатком другого куска. В новых сплавах процентное содержание меди стало одинаковым. Какова масса каждого из отрезанных кусков?

Решение: Пусть с₁ и с₂ — концентрации меди соответственно в первом и втором сплавах, а х — массы отдельных кусков сплавов. Тогда масса меди в первом сплаве составляет с₁т, во втором — с₂п. В отделенном куске х от первого сплава меди содержится c_l x, а в куске от второго сплава — с₂х. После того как каждый сплав сплавили с куском другого сплава, в первом сплаве меди стало с₁ т - с₁ х + с₂х, а во втором — с₂п- с₂х + c_lx. Приравнивая новые концентрации сплавов, получаем уравнение:

_

Таким образом, получим одно уравнение с тремя неизвестными с₁ , с₂ и х. Избавившись от знаменателей, перенеся все величины влево и перегруппировав их, находим: (с₁ - с₂ )(тп – х (т + п)) = 0.

Так как по условию с₁ ≠ с₂, то имеем: . Легко проверить, что х < т и х < п, поэтому найденное значение яв­ляется ответом.

Ответ: отрезали кг.

Задача 23. Стройотряд состоит из 32 бойцов, каждый из которых владеет одной или двумя строительными профессиями: каменщик, бетонщик и плотник. Плотников в 2 раза больше, чем бетонщиков, и в n раз меньше, чем каменщиков (3 ≤ n ≤ 20, n – натуральное число.). Сколько бойцов в отряде владеет только одной профессией, если число бойцов, владеющих двумя профессиями, на 2 больше, чем число бойцов, владеющих профессией плотника?

Решение: Пусть х – число бойцов, владеющих одной профессией, у – двумя, u - число плотников среди бойцов отряда, v - число бетонщиков, w - число каменщиков, так как всего бойцов 32, то х + у = 32. по условию u = 2v, w = nu, y= u + 2. таким образом, получаем четыре уравнения и шесть неизвестных. Пятое уравнение получаем из условия равенства специальностей. С одной стороны, их количество равно х + 2у, а с другой – u+ v + w, т. е. х + 2у = u+ v + w. Выразим в уравнениях неизвестные через u:

v = u/2, w = nu, y = г +2, х = 30 – u и подставим в последнее уравнение, получим: 34 = u .нечетное натуральное число 2n+1 должно быть среди делителей числа 68. Оно единственное и 2n + 1=17, n = 8. (n удовлетворяет условию, наложенному на него). Тогда u = 4, х = 26.

Ответ: в отряде 26 бойцов, владеющих только одной профессией.

Задача 24. Два поезда отправляются навстречу друг другу с постоянными скоростями, один их А в В, другой из В в А. Они могут встретиться на на середине пути, если поезд из А отправиться на 1,5 часа раньше. Если бы оба поезда вышли одновременно, то через 6 часов расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? [2, с.106]

Решение: Пусть расстояние между А и В равно s, а скорости поездов, идущих из А в В и из В в А соответственно равны v₁ и v₂. Если поезд из А отправился на 1,5 часа раньше, то за это время он прошел бы расстояние 1,5v₁, и между поездами было бы расстояние (s-1,5v₁). Тогда время встречи поездов определяется по формуле: _. За это время поезд из В в А проходит половину пути, т. е. : .

Если бы оба поезда вышли одновременно, то за 6 часов они прошли бы расстояние 6v₁ и 6v₂. Между ними оставалось бы расстояние, равное десятой части первоначального, т. е. за 6 часов вместе они прошли бы 0,9 всего расстояния. Поэтому 6v₁ + 6v₂= 0,9s. Итак, имеем систему двух уравнений с тремя неизвестными:

профессией плотника?адеющих дв профессиями: каменщик, бетонщик и плотн

В условии же требуется найти время, за которое каждый поезд проходит весь путь, т. е. . Разделим обе части первого уравнения на s² , а второго на s. Обозначим: получим систему двух уравнений с двумя неизвестными:

х – у = 3ху,

6х +6у = 0,9.

Выразив из второго уравнения у и подставив в первое уравнение, получим следующее уравнение:

3х² - 2,45х - 0,15 = 0. Оно имеет корни: . Поскольку у > 0, то подходит только первая пара.

Ответ: поезд, идущий из В в А, затрачивает на весь путь 12 ч, а поезд, идущий из А в В – 15ч.