Основные этапы узлового метода для моделирования систем с сосредоточенными параметрами.

1. В качестве базисных координат будем использовать разность потенциалов между базовыми и небазовыми узлами.

2. В качестве топологических уравнений, описывающих уравнение токов в узлах, используют уравнение:

.

Эти уравнения при разделении ветвей по типам можно переписать:

(3)

3. К этим топологическим уравнениям добавим компонентные уравнения, которые для соответствующих типов элементов имеют вид:

(4)

(5)

(6)

где

- разности потенциалов на реальных ветвях дерева ориентированного графа эквивалентной схемы.

4. Подставляя (4), (5), (6) в уравнение (3) получим:

Как видно, вектор неизвестной входит и под знак производной и под знак интеграла. Такие уравнения называются интегро-дифференциальными.

5. Выполним дискретизацию этих уравнений, т.е. заменим 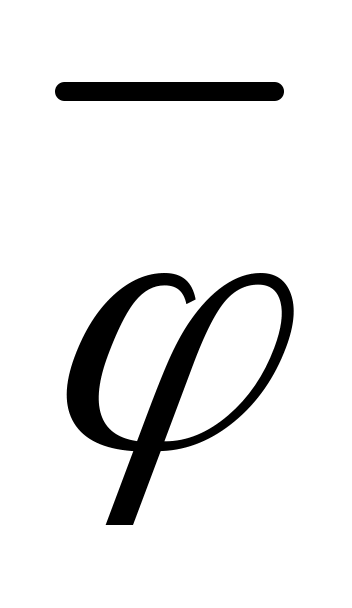разностными выражениями, в которых будет участвовать значение этой неизвестной функции в дискретных точках.

,

где

- шаг дискретизации.

где

- время.

(7)

(8)

Подставим в уравнение (3), получим:

Учтем соотношение и сгруппируем величины для n-го момента времени в левой части уравнения, а для (n-1)–го в правой, тогда получим:

(9)

(10)

где

- const матрица

-в общем случае нелинейно зависит от .

- вектор (для каждого момента времени свой).

Частные случаи:

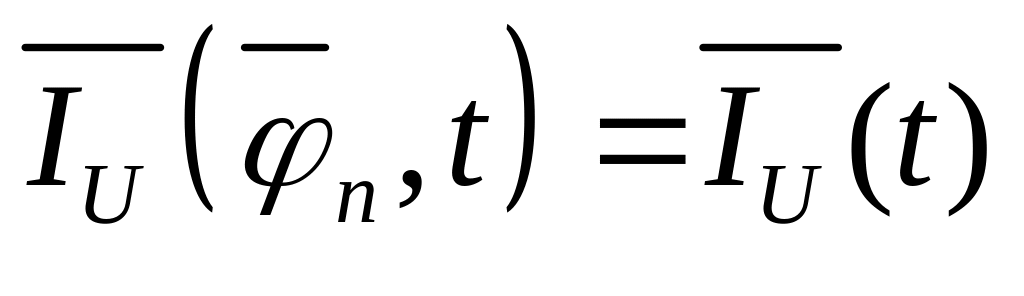1. , тогда уравнение (10) перепишется в виде:

(11)

Это система линейных алгебраических уравнений, где неизвестными являются компоненты .

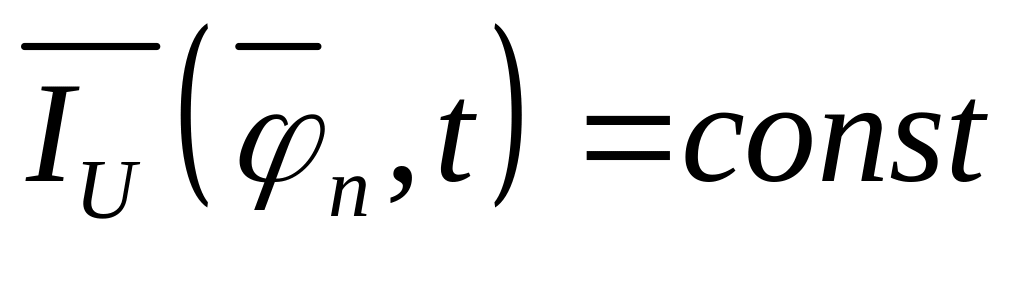2. это частный случай первого.

Пример получения матрицы инциденций электрической подсистемы:

Дана электрическая схема (см. рис.1).

Рис.1 Электрическая схема

Составим эквивалентную к ней (см. рис.2).

Рис.2 Эквивалентная схема

Матрицы инциденции для элементов R и C:

Понятие о моделях теории массового обслуживания

Используемые в настоящее время в локальных сетях протоколы канального уровня используют методы доступа к среде, основанные на ее совместном использовании несколькими узлами за счет разделения во времени. В этом случае, как и во всех случаях разделения ресурсов со случайным потоком запросов, могут возникать очереди. Для описания этого процесса обычно используются модели теории массового обслуживания.

Механизм разделения среды протокола Ethernet упрощенно описывается простейшей моделью типа M/M/1 - одноканальной моделью с пуассоновским потоком заявок и показательным законом распределения времени обслуживания. Она хорошо описывает процесс обработки случайно поступающих заявок на обслуживание системами с одним обслуживающим прибором со случайным временем обслуживания и буфером для хранения поступающих заявок на время, пока обслуживающий прибор занят выполнением другой заявки (рисунок 1). Передающая среда Ethernet представлена в этой модели обслуживающим прибором, а пакеты соответствуют заявкам.

Введем обозначения: l - интенсивность поступления заявок, в данном случае это среднее число пакетов, претендующих на передачу в среде в единицу времени, b - среднее время обслуживания заявки (без учета времени ожидания обслуживания), то есть среднее время передачи пакета в среде с учетом паузы между пакетами в 9.6 мкс, r - коэффициент загрузки обслуживающего прибора, в данном случае это коэффициент использования среды, r = lb.

В теории массового обслуживания для данной модели получены следующие результаты: среднее время ожидания заявки в очереди (время ожидания пакетом доступа к среде) W равно:

Рис. 1. Применение модели теории массового обслуживания M/M/1 для анализа трафика в сети Ethernet

Компонентные уравнения в составе математическй модели

Технический объект состоит из каких-то частей(узлов, элементов) каждый из которых может обладать своими, присущими ему свойствами. Эти компоненты связаны между собой и их взаимодействие порождает сам технический объект. Такому устройству самого объекта соответствует “устройство” математической модели.

Математическую модель можно рассматривать как:

1. часть, описывающую структуру технического объекта (в данном контексте “структура” является синонимом “топология”. Поэтому соответствующие уравнения в математической модели называют структурными или топологическими). Способы их получения мы рассмотрим позже.

2. часть, представленная уравнениями, описывающими поведение отдельных элементов, компонентов из которых состоит технический объект. Такие уравнения называются поэтому компонентными. Чем больше количество компонентов, которые мы сможем описать с помощью уравнений, тем более широкий спектр технических объектов мы сможем в дальнейшем моделировать.

Оказывается, в тоже время, что компоненты, имеющие различную физическую природу могут описываться одинаковыми по виду математическими уравнениями. Простейшим примером из этого ряда является дифференциальное уравнение, которое с одной стороны описывает движение материальной точки массы m на пружине жесткостью k(см. рис.1а)

а) б)

Рис.1

А с другой стороны, если придать другой смысл параметрам m и k, соответственно электрическая емкость и индуктивность соленоидальной катушки, соединенных параллельно(см. рис.1б), то уравнение такого же вида будет описывать динамику изменения электрического заряда на пластинах конденсатора.

В этом случае эти уравнения оказываются одинаковыми по виду так как в обеих ситуациях они соответствуют процессу изменения энергии(в первом случае потенциальная энергия растянутой пружины “перетекает” в кинетическую энергию материальной точки, во втором случае энергия магнитного поля соленоидальной катушки “перетекает” поля между пластинами конденсатора). Оказывается что и для других физических процессов могут бать записаны одинаковые по виду уравнения. В основе этого факта лежит философский принцип единства мира. Исходя из этого вытекает следующая идея: построить такое программное обеспечение, которое единообразно описывало бы поведение компонентов разной природы, если в математическом плане им соответствуют одни и те же уравнения. В качестве примера такого подхода продемонстрируем соответствие механической и электрической систем для трех типов элементов.

Эти элементы в соответствии с терминологией, принятой для электрических систем, будем обозначать

А. Элемент типа R(соответствует рассеиванию энергии в электрической системе) – резистор.

Б. Элемент типа C – электрический конденсатор.

В. Элемент типа L – индуктивность.

Запишем компонентные уравнения для различных типов подсистем.

1. Электрическая подсистема

А. Уравнение сопротивления

.

Б. Уравнение электрической емкости

.

В. Уравнение электрической индуктивности

.

2. Механическая поступательная подсистема

А. Уравнение вязкого трения

,

если принять , то

.

Таким образом, мы видим, что при переходе от системы к системе I переходит в V, а U переходит в F.

Б. Уравнение пружины

если теперь взять производную по времени, получим

.

В. Уравнение массы

.

Аналоги компонентов для различных видов подсистем

Можно показать, что и для других видов подсистем можно сформулировать такие же по структуре уравнения.

Подсистема	Фазовые координаты		Компоненты
	Типа поток	Типа потенциал	Типа R	Типа C	Типа L
Электрическая	Ток	Напряжение	Электрическое сопротивление	Электрическая емкость	Электрическая индуктивность
Механическая поступательная	Сила	Линейная скорость	Трение	Масса	Податливость
Механическая с вращательным движением	Момент	Угловая скорость	Трение	Момент инерции	Крутильная податливость
Гидравлическая (пневматическая)	Расход	Давление	Трение	Гидравлическая емкость	Гидравлическая индуктивность
Тепловая	Тепловой поток	Температура	Тепло-сопротивление	Теплоемкость	________

Кроме рассмотренных трех типов элементов можно ввести и следующие: элемент, соответствующий источнику тока, элемент, соответствующий источнику ЭДС. Точно также в механической системе обычно приходится вводить элемент, соответствующий источнику внешней силы. Все рассмотренные элементы представляют собой так называемые двухполюсники, то есть элементы, взаимодействующие между собой лишь в двух точках.

Обычно используют следующие графические отображения этих элементов.

Д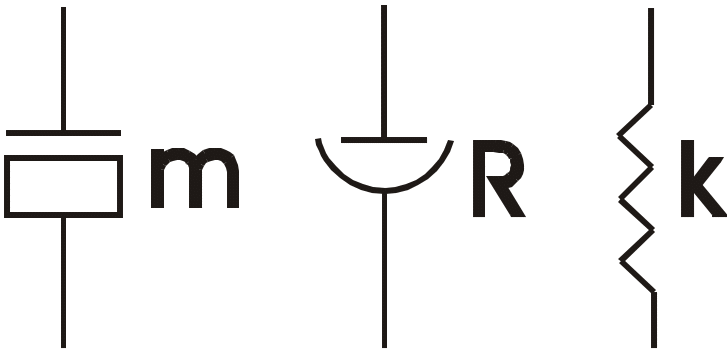 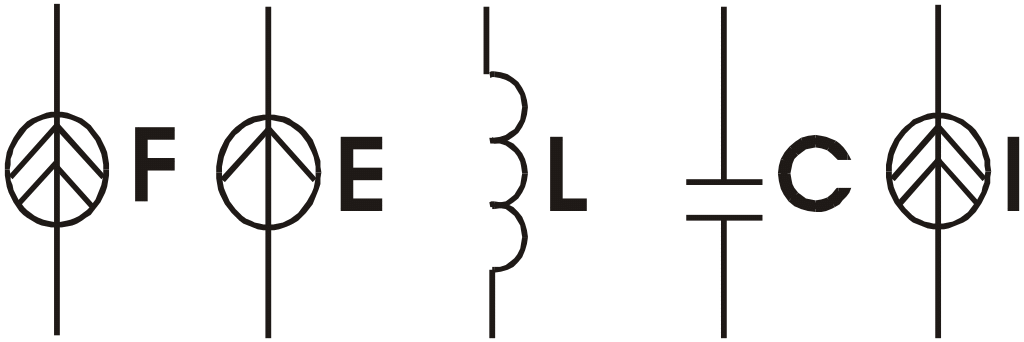ля механической системы рис.2(а-г)

а) б) в) г) д) е) ж) з)

и)

рис.2

Для электрической системы рис.2(д-и)