Получение топологических уравнений.

Топологические уравнения описывают связь элементов между собой. Для их получения необходимо изобразить эквивалентную схему объекта.

Одним из способов описания топологических уравнений является способ записи уравнений непрерывности, равновесия или других уравнений, выражающих законы сохранения.

Топологические уравнения для электрической подсистемы:

3. Уравнение 1-го закона Кирхгофа:

(сумма токов в узле схемы равна нулю).

- ток в k-ой ветви,

р – множество номеров ветвей инцидентных к данному узлу.

4. Уравнение 2-го закона Кирхгофа:

(сумма падений напряжений по любому замкнутому контуру равна нулю).

j – номер ветви,

q – множество номеров ветвей в рассматриваемом контуре.

С использованием М-матрицы эти уравнения примут вид:

(1)

(2)

Связь матрицы инциденций и М- матрицы для ориентированного графа.

Узловой метод получения математической модели системы.

Метод связан с электрическими подсистемами. Этот метод применяется и в других системных областях.

Вектором базисных координат является вектор переменных типа узловых потенциалов.

В качестве топологических уравнений используем 1-ый закон Кирхгофа:

,

где

- вектор типа узловых потенциалов.

Для этого в ориентированный граф объекта, соответствующий его эквивалентной схеме, вводятся фиктивные ветви. Проводимости этих ветвей полагают равными нулю, следовательно, токи в них отсутствуют.

Совокупность этих фиктивных ветвей образуют дерево.

Пример:

Матрица инциденции:

	а	б	в	г	д	е	ж	з	и
1	-1	1	0	0	0	0	0	0	0
2	0	-1	1	1	0	0	0	0	0
3	0	0	-1	0	1	1	0	0	0
4	0	0	0	-1	-1	0	1	0	0
5	0	0	0	0	0	-1	0	1	1
6	0	0	0	0	0	0	-1	-1	0

М-матрица:

	Ветви дерева
Хорды		к	л	м	о	н	р
	а	1	0	0	0	0	0
	б	-1	1	0	0	0	0
	в	0	-1	1	0	0	0
	г	0	-1	0	1	0	0
	д	0	0	-1	1	0	0
	е	0	0	-1	0	1	0
	ж	0	0	0	-1	0	1
	з	0	0	0	0	-1	1
	и	0	0	0	0	-1	0

Т.к. токи в ветвях дерева равны нулю, следовательно, уравнение

(2) примет вид:

, где

- токи в реальных ветвях (сейчас они являются хордами).

Из уравнения (1) получим уравнение связи переменных типа потенциала (каждая компонента которого представляет собой разность потенциалов между i-ым не базовым узлом и потенциалом базового узла):

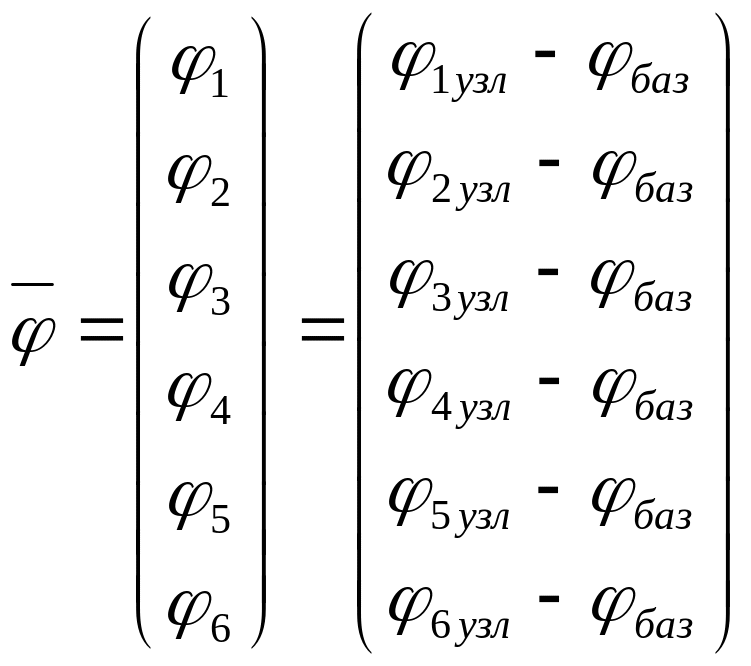
При рассмотрении реальных систем используют подход, в котором матрицы A и I разбивают на подматрицы, соответствующие элементам R, C, L в цепи:

, или

Пример получения матрицы инциденций электрической подсистемы:

Дана электрическая схема (см. рис.1).

Рис.1 Электрическая схема

Составим эквивалентную к ней (см. рис.2).

Рис.2 Эквивалентная схема

Матрицы инциденции для элементов R и C:

Узловой метод получения математической модели системы