Получение топологических уравнений.
Топологические уравнения описывают связь элементов между собой. Для их получения необходимо изобразить эквивалентную схему объекта.
Одним из способов описания топологических уравнений является способ записи уравнений непрерывности, равновесия или других уравнений, выражающих законы сохранения.
Топологические уравнения для электрической подсистемы:
Уравнение 1-го закона Кирхгофа:
(сумма токов в узле схемы равна нулю).
-
ток в k-ой
ветви,
р – множество номеров ветвей инцидентных к данному узлу.
Уравнение 2-го закона Кирхгофа:
(сумма падений напряжений по любому замкнутому контуру равна нулю).
j – номер ветви,
q – множество номеров ветвей в рассматриваемом контуре.
Запись топологических уравнений с помощью матрицы контуров и сечений.
Матрица контуров и сечений (М-матрица) строится на основании ориентированного графа расчетной схемы технического объекта.
Необходимо предварительно в этом графе выбрать его дерево. Деревом называется такой подграф рассматриваемого графа, который содержит все его вершины и не имеет циклов.
Циклом называется любой замкнутый путь в графе.
Хордой называется ветвь графа, не вошедшая в его дерево.
Количество столбцов М-матрицы соответствует числу ветвей дерева, а количество строк – числу хорд.
Процедура формирования М-матрицы заключается в следующем:
К дереву графа поочередно подключается каждая его хорда, при этом возникает цикл.
Выполняется обход этого цикла в направлении заданном направлением хорды.
В строке матрицы соответствующей заданной хорде ставиться:
+1, если направление хорды совпадает с направлением текущей ветви.
-1, если направление противоположное.
0, если ветвь не вошла в заданный контур.
Пример:
Рассмотрим следующее дерево:
|
Ветви дерева |
|||||
хорды |
|
б |
г |
д |
е |
ж |
а |
-1 |
0 |
0 |
1 |
-1 |
|
в |
1 |
1 |
0 |
0 |
0 |
|
к |
0 |
0 |
1 |
0 |
0 |
|
и |
0 |
-1 |
-1 |
-1 |
0 |
|
С использованием полученной матрицы запишем уравнения, соответствующие законам Кирхгофа.
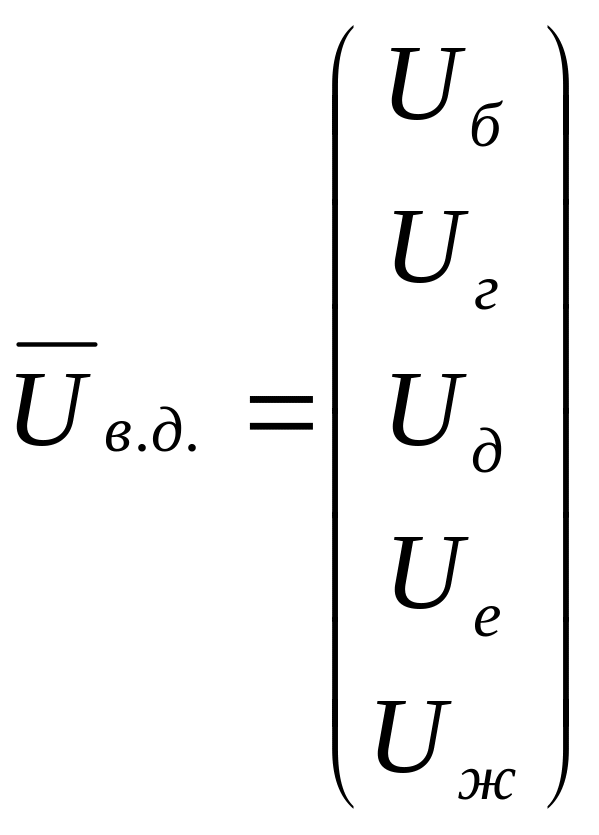
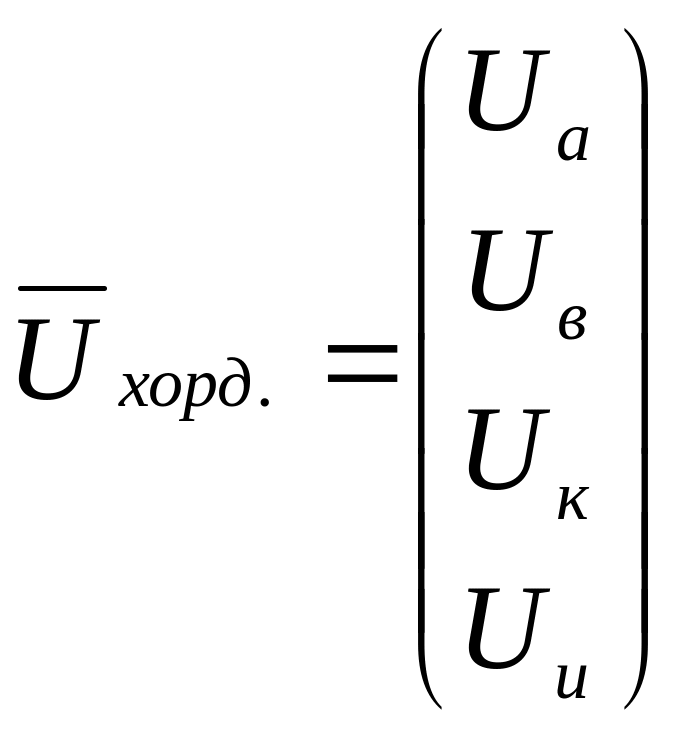
(1)
(2)
В покомпонентном виде уравнение (1) имеет следующий вид:
Как видно, уравнения этой системы являются выражением 2-го закона Кирхгофа для соответствующих замкнутых контуров.
Также уравнение (2) является выражением 1-го закона Кирхгофа:
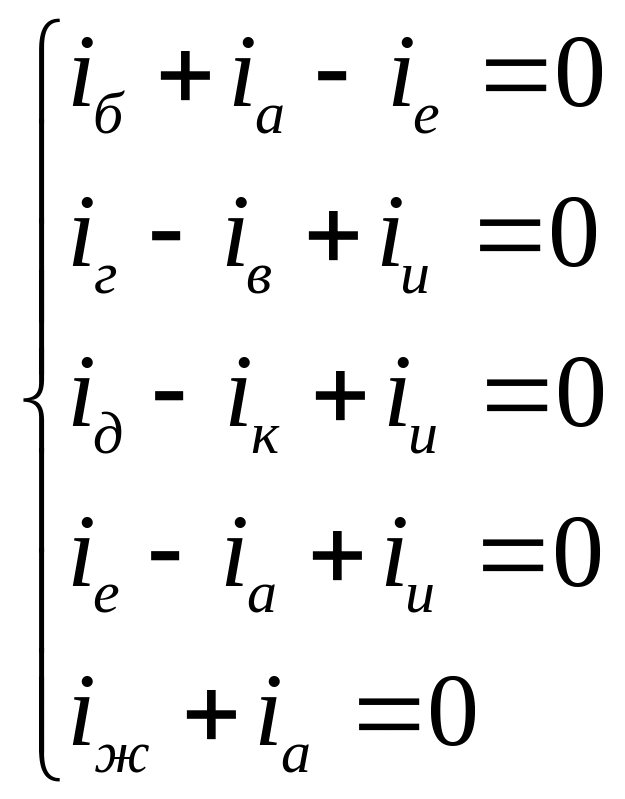
-например, для 6-го узла.
-например, для 1-го узла
Использование матрицы инциденций для описания структуры системы.
Связь матрицы инциденций и М- матрицы для ориентированного графа.
Пример получения матрицы инциденций электрической подсистемы.
Важным для системного подхода является определение структуры системы, понимаемой как совокупность связей между элементами, отражающими их взаимодействие. Наиболее общее – топологическое описание структуры – позволяет в самом общем виде определить составные части системы и формализуется с помощью теории графов.
Использование матрицы инциденций для описания структуры системы.
Поведение различных по своей природе объектов может быть описано одинаковыми по своей структуре уравнениями. Это лежит в основе построения программных комплексов САПР в различных предметных областях. Идея заключается в том, что объект разбивается на подсистемы:
механические;
электрические;
пневматические;
гидравлические и др.
Каждая из подсистем состоит из конечного набора элементов. Уравнения, описывающие поведение отдельного элемента, должны быть заранее получены и реализованы в процедурах.
Связь между элементами подсистемы записывается с помощью топологических уравнений.