Лекция № 5 Тема: Оценка параметров распределения.

План:

1. Выборочные оценки параметров случайной величины. Основные требования к оценкам.

2. Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации.

1. Выборочные оценки параметров случайной величины. Основные требования к оценкам

На практике эти параметры находятся приближенно по данным опыта.

Пусть с испытанием связана случайная величина с неизвестным параметром , и пусть в результате серии независимых испытаний получена выборка . В качестве приближенного значения параметра принимают надлежащим образом выбранную комбинацию элементов выборки .

.

Величина называется выборочной оценкой параметра .

К выборочным оценкам предъявляются следующие три основных требования: состоятельность, несмещенность, эффективность.

Чтобы были понятны даваемые далее определения этих понятий, обратим внимание на следующее: до выполнения испытаний числа представляют собой независимые случайные величины, подчиненные одному и тому же закону распределения, совпадающему с законом распределения случайной величины , поэтому также является случайной величиной, и имеет смысл говорить о математическом ожидании, дисперсии, СКО и т.д. случайной величины .

2. Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации

Для выполнения инженерных расчетов, связанных с прогнозированием по массовым случайным явлениям и основанных на методах теории вероятностей, необходимо знать параметры случайных величин, участвующих в этих расчетах: математическое ожидание, дисперсию и т.д.

1. Оценка называется состоятельной, если при неограниченном увеличении объема выборки сходится по вероятности к истинному значению параметра :

Это означает: при достаточно большом объеме выборки с практической достоверностью (с вероятностью, близкой к единице) практически совпадает с истинным значением .

2. Оценка называется несмещенной, если ее математическое ожидание совпадает с истинным значением параметра : .

3. Оценка называется эффективной, если она несмещенная и при этом имеет наименьшую дисперсию (наименьший разброс относительно ) по сравнению с другими несмещенными оценками параметра .

Пусть с испытанием связана случайная величина с неизвестными числовыми характеристиками (а, D) и пусть набрана независимая выборка .

В дальнейшем будем употреблять следующий удобный термин: любую функцию от выборки будем называть статистикой.

Лемма 1. Статистика

является состоятельной несмещенной оценкой математического ожидания а.

Доказательство

1. Мы знаем, что элементы выборки являются независимыми случайными величинами с одним и тем же законом распределения, совпадающим с законом распределения случайной величины , а значит, имеют те же числовые характеристики (а, D).

По теореме Чебышева среднее арифметическое независимых случайных величин с одинаковыми параметрами (а, D), при неограниченном возрастании числа слагаемых сходится по вероятности к общему математическому ожиданию

что и означает состоятельность оценки.

2. Имеем

Это означает несмещенность оценки .

Л емма 2. Статистика

является состоятельной несмещенной оценкой дисперсии D. (Доказывается аналогично лемме 1).

Замечание 1. Если в формуле заменить (n - 1) на n , то оценка останется состоятельной, но будет смещенной. Величина S² называется исправленной дисперсией.

Замечание 2. Из леммы 2 следует, что статистика:

является состоятельной оценкой для СКО ). Можно доказать, что , т.е. оценка S является смещенной оценкой для .

Пусть по данным опыта получим ряд значений случайной точки ( ) (выборка):

(х₁, у₁) (х₂, у₂), …, (х_n, у_n).

Справедлива следующая

Лемма 3. Состоятельной несмещенной оценкой для cov( ) является выборочная ковариация

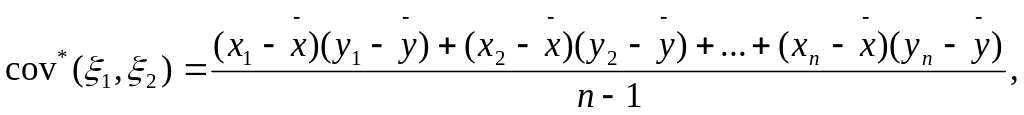
где