
- •Вступ………………………………………….……6
- •Ба жаю вам успіхів у пізнанні нового і цікавого !
- •Перпендикулярні прямі
- •Як промені з'єднуються в кути
- •Місток через чорнильне море
- •На алеї чотирикутників
- •Про коло та круг
- •Навчитись вимірювати, порівнювати — дуже важливо
- •Довжину вимірюємо не лише мотузкою
- •Що означає «виміряти площу»?
- •Література
Перпендикулярні прямі
Внаслідок перетину двох прямих утворюється чотири кути. Якщо один із кутів прямий, тоді і всі інші три кути прямі.

У цьому разі говорять, що прямі перетинаються під прямим кутом.
Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Перпендикулярність
прямих АВ і CD
позначають знаком
![]() .
.
Записують: АВ CD і говорять: «Пряма АВ перпендикулярна до прямої СD»
 На
малюнках показано, як за допомогою
транспортира і лінійки побудувати пряму
б,
перпендикулярну
до прямої а.
На
малюнках показано, як за допомогою
транспортира і лінійки побудувати пряму
б,
перпендикулярну
до прямої а.

Через будь-яку точку, яка не лежить на прямій, проходить тільки одна пряма, перпендикулярна до даної прямої.
Промені або відрізки, що лежать на перпендику- лярних прямих, є також перпендикулярними.
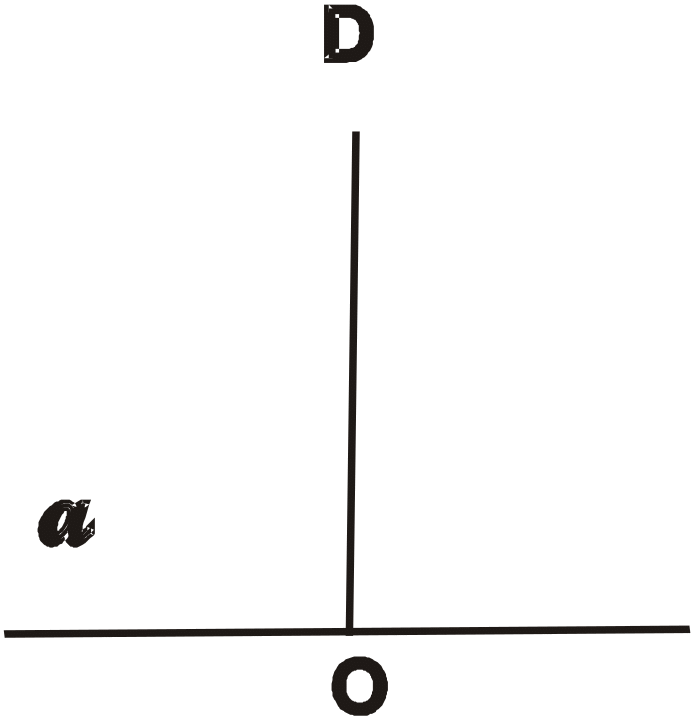 Відрізок
прямої, перпендикулярної до даної
прямої, який має одним зі своїх кінців
точку їх перетину називається
перпендикуляром
до
даної
прямої.
Точка їх перетину називається основою
перпендикуляра.
Відрізок
прямої, перпендикулярної до даної
прямої, який має одним зі своїх кінців
точку їх перетину називається
перпендикуляром
до
даної
прямої.
Точка їх перетину називається основою
перпендикуляра.

П еревір себе:
Які прямі називаються паралельними?
Як побудувати пряму, паралельну даній?
Які прямі називаються перпендикулярними?
Як побудувати пряму, перпендикулярну до даної прямої за допомогою: а)транспортира і лінійки;
б) косинця?
Що таке перпендикуляр до прямої ?
1.На малюнках зображено пари прямих. Запишіть прямі, які:
1) перетинаються;
2) паралельні.


2.Проведіть пряму а. Позначте точку А, що не лежить на цій прямій. За допомогою лінійки і косинця проведіть пряму b, паралельну прямій а.
Проведіть паралельні прямі а і b так, як показано на малюнку.

Через точку О проведіть пряму с, паралельну прямій b. За допомогою лінійки і косинця перевірте, чи паралельні прямі а і с.
4.Поясніть, як зігнути аркуш паперу, щоб лінія згину була паралельною краю аркуша.

 5.Чи
є дані прямі паралельними ?
5.Чи
є дані прямі паралельними ?
6. На малюнках зображено пари прямих. Запишіть:
1) перпендикулярні прямі;
2) не перпендикулярні прямі.

7.На якому з малюнків:
відрізок АВ перпендикулярний до прямої а;
2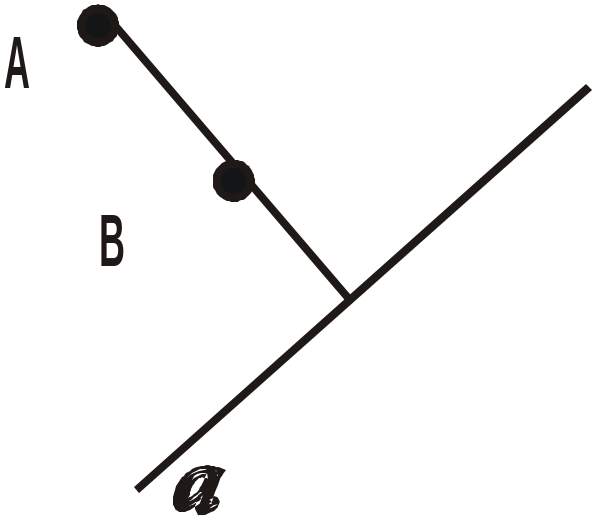 )
відрізок АВ
є
перпендикуляром до прямої а.
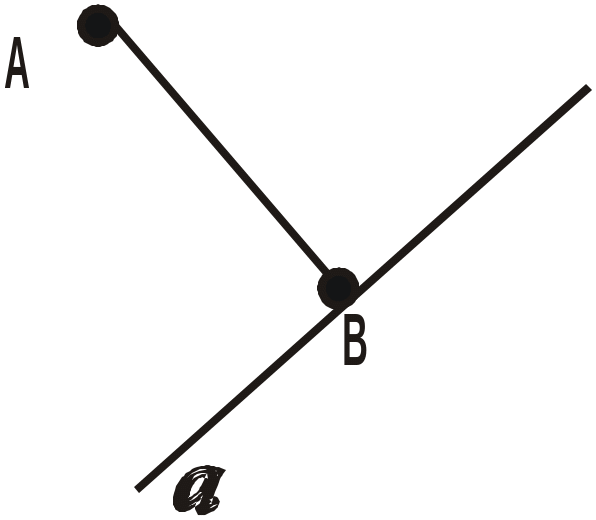
)
відрізок АВ
є
перпендикуляром до прямої а.
8.Проведіть пряму а. За допомогою косинця побудуйте пряму b, перпендикулярну до прямої а.
9.Побудуйте в зошиті прямі а і b так, які є перпендикулярними прямими.
10.Роздивіться і скажіть, де в класній кімнаті ви бачите :
а) паралельні прямі ;
в) перпендикулярні.
11.Проведіть пряму а і позначте точку В, яка не лежить на прямій. Проведіть з цієї точки перпендикуляр на пряму а.
12.Побудуйте перпендикулярні прямі по клітинках зошита.
13.Побудуйте перпендикулярні прямі за допомогою косинця.
У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
паралельні прямі;
перпендикулярні прямі;
перпендикуляр
ви дізналися :
про паралельні та перпендикулярні прямі
ви навчилися :
розпізнавати та називати паралельні та перпендикулярні прямі;
зображувати схематично (за допомогою косинця і лінійки) паралельні та перпендикулярні прямі.

Позначимо три точки, наприклад А, В, С, що не лежать на одній прямій, і сполучимо їх відрізками. Дістанемо геометричну фігуру - трикутник.

Точки А, В, С - вершини трикутника, а відрізки АВ, ВС, СА – його сторони.
Трикутником називається геометрична фігура, яка складається з трьох точок, що не лежать на одній прямій і трьох відрізків, що сполучають їх.
Записуємо: ∆ АВС і говоримо: «трикутник ABC».
У назві трикутника букви можна записати і в іншому порядку:
∆ ВСА, ∆ СВА, ∆ САВ.

Кути ABC, ВСА, CAB - це кути трикутника ABC, їх ще можна позначити маленькими грецькими буквами α ,β ,γ.
Сторони трикутника ABC можна позначити й маленькими буквами а, b, с. При цьому дотримуються правила: проти кута ВАС лежить сторона а, проти кута АВС – сторона b , проти кута ВСА - сторона с.

Трикутники класифікують (розрізняють між собою) за довжинами сторін та мірами кутів.
Залежно від довжин сторін трикутники поділяють на такі види:
• різносторонні, якщо всі сторони мають різну довжину ;

АВ≠ВС≠СА
• рівносторонні, якщо всі сторони рівні ;

АВ=ВС=СА
•рівнобедрені, якщо дві сторони рівні.

АВ =ВС
Рівнобедреним називається трикутник, у якого дві сторони рівні.
Рівні сторони рівнобедреного трикутника називають бічними сторонами, а третю його сторону - основою.

У рівнобедреному трикутнику кути при основі рівні.

З алежно від міри кутів трикутники поділяють на такі види:
гострокутні, якщо всі кути гострі ;
• тупокутні, якщо один з кутів тупий ;

•прямокутні, якщо один з кутів прямий , тобто
90°.

Висотою трикутника називається відрізок, проведений до протилежної сторони трикутника під прямим кутом, тобто 90°.

Бісектрисою трикутника називається відрізок бісектриси кута, що сполучає цю вершину з точкою на протилежній стороні і ділить цей кут пополам.
На малюнку ви бачите ∆ АВС і його бісектрису, яка виходить з ВАС і ділить його пополам.

Периметр трикутника
Суму довжин усіх сторін трикутника називають його периметром.
Периметр позначають буквою Р.
Тобто Р∆ АВС= АВ+ВС+СА
Те, що периметр трикутника ABC дорівнює 50 см, коротко можна записати так:
Р∆ АВС = 50 см
Перевір себе:
Яку фігуру називають трикутником?
Які трикутники називають: прямокутними; гострокутними; тупокутними? Наведи приклади.
Які трикутники називають рівнобедреними?
Як знайти периметр трикутника?
Як називають трикутники залежно від довжин їх сторін?
Які сторони рівнобедреного трикутника називаються бічними сторонами?
1 .Назвіть
трикутники, зображені на малюнку. Яка
сторона лежить проти кута С?
Назвіть
сторони, прилеглі до кута С
.
.Назвіть
трикутники, зображені на малюнку. Яка
сторона лежить проти кута С?
Назвіть
сторони, прилеглі до кута С
.
2.Накресліть трикутник АВС. Назвіть:
сторони, які лежать проти кутів А і В;
кути, які лежать проти сторін АВ і ВС;
кути, прилеглі до сторони АВ;
кут, що лежить між сторонами АС і ВС.
3.На малюнку сторони трикутника позначено маленькими буквами. Які назви мають вершини трикутника?
Накресліть трикутник і позначте його вершини D,E,F. Назвіть сторони і кути трикутника. Позначте сторони трикутника маленькими буквами.
5.Побудуйте за клітинками трикутник:
1) рівнобедрений; 3) прямокутний;
2) гострокутний; 4) тупокутний.
6.Побудуйте трикутник АВС і за допомогою транспортира і лінійки проведіть його бісектрису.
7.Побудуйте трикутник KLM і за допомогою косинця проведіть його висоту.
8. Побудуйте довільний трикутник. За допомогою транспортира і лінійки проведіть його бісектриси. Позначте точку перетину бісектрис трикутника.
9.Побудуйте гострокутний трикутник. За допомогою косинця проведіть висоти трикутника. Позначте точку їх перетину.
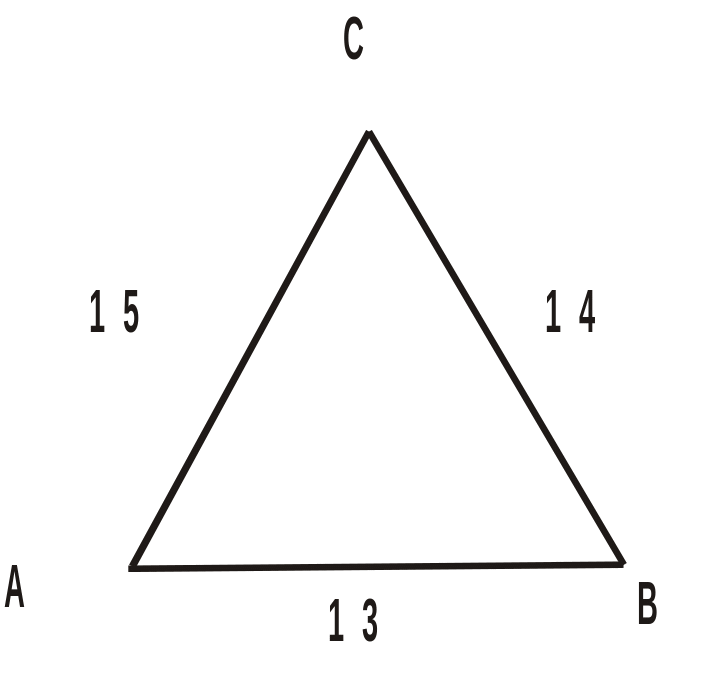 10.
Знайдіть периметр даного трикутника.
10.
Знайдіть периметр даного трикутника.
11.Знайдіть сторони рівностороннього трикутника, якщо його периметр дорівнює:
1) 36 см;
2) 45 см;
3) 72 см.
12.Знайдіть периметр рівнобедреного трикутника з основою а і бічною b стороною, якщо:
1) а = 14 см, b = 12 см;
2) а= 16 см, b =17 см;
3) а= 8 см, b = 5 см.
13. Який вид трикутника, якщо один з його кутів дорівнює:
1)90°;
2) 141°;
3)95°?
14.Накресліть рівнобедрений прямокутний трикутник KLM.
15. Одна сторона трикутника дорівнює 10 см, друга – 14 см, а третя більша за другу на 2 см. Знайдіть периметр трикутника.
16. Основа рівнобедреного трикутника дорівнює 10 см, а його бічна сторона на 3 см більша. Знайдіть периметр трикутника.
1 7. Накресліть довільний трикутник. Перетніть його двома прямими так, щоб на малюнку утворилось 3 трикутники.
18. Одна сторона трикутника дорівнює 7 см, друга сторона у 2 рази більша за першу, а третя – на 4 см менша за другу. Знайдіть периметр трикутника.
19. Запишіть, скільки на малюнку трикутників.

20. Визначте вид трикутників.

21. Скільки трикутників ви бачите на малюнку.

У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
трикутник;
периметр трикутника;
висота ;
бісектриса трикутника ;
ви дізналися:
про трикутник та його види ;
ви навчилися:
• розпізнавати трикутник та його види
( рівносторонній, різносторонніій, рівнобедрений, прямокутний, тупокутний);
• обчислювати периметр трикутника ;

Вивчаючи навколишній світ, ми часто бачимо симетрію. Симетрія – це таке розміщення точок або частин предмета у просторі, коли одна їх половина є ніби дзеркальним відображенням другої. Приклади прояву симетрії показано на малюнку. Вона досить поширена у природі. Її можна спостерігати у формі листків і квітів рослин.

 А
також у розміщенні різних органів
тварин, у формі кристалічних тіл .
А
також у розміщенні різних органів
тварин, у формі кристалічних тіл .
 Симетрія
широко застосовується на практиці, в
будівництві, в техніці .
Симетрія
широко застосовується на практиці, в
будівництві, в техніці .

Коли аркуш, на якому зображені предмети чи геометричні фігури,зігнути за уявною лінією, ми побачимо, що і предмети, і фігури зливаються в одне ціле всіма точками. Отже, лінія на малюнку, яка розділяє його на дві однакові, але дзеркально відображені (протиле-
жні) частини є віссю симетрії.
Кажуть, що дві фігури симетричні відносно прямої, якщо кожна з них складається з точок, симетричним точкам другої фігури.
На малюнку зображено два кола, симетричні одне одному відносно прямої а. Точки А і В, які є центрами
 цих
кіл, також симетричні відносно прямої
а.
У
такому . випадку
відстані АК
і
КВ
рівні
між собою.
цих
кіл, також симетричні відносно прямої
а.
У
такому . випадку
відстані АК
і
КВ
рівні
між собою.

Об'єкти, які мають вісь або центр симетрії, легко сприймаються і приємні для ока. Недарма в Стародавній Греції слово «симетрія» слугувало синонімом слів «гармонія», «краса».Ідея симетрії широко використовується в образотворчому мистецтві, архітектурі й техніці. Хіміки й фізики говорять про симетрію явищ. Можна знайти прояви симетрії в музиці й поезії.

Багато геометричних фігур те ж мають вісь
 На
малюнку зображено рівнобедрений
трикутник. Пряма, яка містить його
висоту, проведену до основи, є
віссю симетрії трикутника.
На
малюнку зображено рівнобедрений
трикутник. Пряма, яка містить його
висоту, проведену до основи, є
віссю симетрії трикутника.
Будь-який кут має вісь симетрії — це пряма, яка містить його бісектрису .

 Рівносторонній
трикутник має три осі симетрії
Рівносторонній
трикутник має три осі симетрії
 Наведемо
приклади фігур, які мають центр симетрії.
Центром симетрії відрізка є його
середина. Точка перетину діагоналей
паралелограма є його центром симетрії
Наведемо
приклади фігур, які мають центр симетрії.
Центром симетрії відрізка є його
середина. Точка перетину діагоналей
паралелограма є його центром симетрії
Також кажуть, що фігура має центр симетрії.
П еревір себе:
Сформулюйте поняття симетрії
Наведіть приклади фігур, які мають осьову
симетрію
Наведіть приклади симетрії у природі .
Наведіть приклади симетрії у техніці.
Наведіть приклади геометричних фігур, які
мають центральну або осьову симетрії.
1. Прочитайте імена героїв казки «Королівство кривих дзеркал» в дзеркальному відображені: Яло, топсед, нушрок, гурд, абаж, бар, анидаг.
2. Намалюйте відображення в дзеркалі.


3. Проведіть осі симетрії.


4. Проведіть можливі осі симетрій.




5. Визначте центр симетрії фігур, зображених на малюнку.
 6.Які з
фігур, зображених на малюнку, не мають
центр симетрії?
Доведіть правильність своєї думки.
6.Які з
фігур, зображених на малюнку, не мають
центр симетрії?
Доведіть правильність своєї думки.

7.Для довільних точок А, В, К, N площини побудуйте точки, симетричні відносно точки О.
8.Накресліть фігуру, яка мала б центр симетрії.
9.Позначте точки, симетричні точкам А, В, С, К, М відносно точки Р.
10.Побудуйте кілька довільних відрізків. Знайдіть їх центри симетрії.
У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
осьова симетрія ;
центральна симетрія
ви дізналися :
про осьову і центральну симетрії, їх використання людиною та відображення в природі
ви навчилися :
•розпізнавати у розміщенні предмети навколишнього середовища осьову і центральну симетрії

Чотирикутником називається фігура, яка складається з чотирьох точок і чотирьох відрізків, що послідовно їх сполучають.
Дані точки називаються вершинами чотирикутника, а відрізки, що їх сполучають, - сторонами чотирикутника.

Вершини чотирикутника, які є кінцями однієї з його сторін, називаються сусідніми.
А несусідні вершини називаються протилежними.
Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.
Чотирикутник позначають, записуючи його вершини.

Наприклад, даний на малюнку чотирикутник позначають так : АВСD.
Чотирикутник, у якого всі кути прямі, називається прямокутником.

У прямокутника протилежні сторони рівні.
У будь-якого прямокутника діагоналі рівні.
Прямокутник, у якого всі сторони рівні, називається квадратом.

Чотирикутник, у якого кожна сторона дорівнює протилежній стороні, називається паралелограмом.

У паралелограма протилежні сторони рівні і паралельні.

АВ=CD, BC=AD
Паралелограм, у якого всі сторони рівні, називається ромбом.

AB=BC=CD=DA
Діагоналі ромба перетинаються під прямим кутом.

Трапеція — це чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні.

Паралельні сторони називаються основами трапеції.
Непаралельні сторони називаються бічними сторонами. Домовимося висотою трапеції називати перпендикуляр, опущений з довільної точки основи трапеції на другу основу

Сума довжин усіх сторін чотирикутника називається периметром.
 Наприклад,
Р
АВСD
=
АВ + ВС + СD
+ DА
Наприклад,
Р
АВСD
=
АВ + ВС + СD
+ DА
Периметр квадрата і ромба може знаходитись і за іншою формулою, а саме:
Р = 4 а,
оскільки у цих фігур усі сторони рівні.
Периметр прямокутника може знаходитись те ж за іншою формулою, а саме :
Р = 2 а + 2 b, або Р = 2(а+ b)
тому, що протилежні сторони рівні.
а
b
 Перевір
себе:
Перевір
себе:
Яку геометричну фігуру називають чотирикутником?
Що таке прямокутник?
Що таке ромб?
Що таке паралелограм?
Що таке квадрат?
Що таке трапеція?
Які сторони трапеції називаються основами?
Які сторони трапеції називаються бічними сторонами?
Що таке діагональ?
Які вершини називаються сусідніми?
Які вершини називаються протилежними?
1.Побудуйте довільний чотирикутник і назвіть його. Покажіть протилежні сторони і вершини.
2.Знайдіть периметр квадрата зі стороною 5 см.
3.Побудуйте в зошиті за допомогою клітинок ромб KLMN . Знайдіть його периметр.
4.Назвіть види чотирикутників, які ви бачите.
5.Побудуйте трапецію ABCD і проведіть у ній висоту. Позначте її.
6.Побудуйте прямокутник BDAC. Проведіть у ньому діагоналі.
7 .Знайдіть периметр прямокутника, якщо його сторони дорівнюють:
1) 2 см і 3 см;
2) 10 мм і 12 мм ;
3) 5 дм і 10 дм.
8. Знайдіть периметр прямокутника, якщо :
1) одна сторона його дорівнює 4 см, а друга – втричі більша;
2 ) одна сторона його дорівнює 10 см, а друга – вдвічі менша;
3) одна сторона його дорівнює 12 см, а друга – на 4 см більша.
9.Побудуйте довільний прямокутник і діагоналі в ньому. Яка довжина однієї діагоналі? Знайдіть суму обох діагоналей. Що ви можете сказати про діагоналі прямокутника.
10.Розгляньте кожен з малюнків. Порахуйте і скажіть скільки чотирикутників на кожному з малюнків.

11.Побудуйте довільний паралелограм. Знайди його периметр.
12.Побудуйте квадрат ABCD зі стороною 2 см і квадрат KLMN зі стороною 4 см. У скільки разів периметр квадрата ABCD менший за периметр квадрата KLMN?
13.Довжина бічної сторони рівнобедреного трикутника – 6 см, а довжина його основи – на 1 см більша. Накресліть цей трикутник і знайдіть його периметр.
14.Визначте, скільки на малюнках чотирикутників.


15.Знайдіть на малюнку 9 чотирикутників.

16.Знайдіть на малюнку 2 трикутники і 4 чотирикутники. Запишіть буквене позначення чотирикутників.

У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
прямокутник;
квадрат;
паралелограм, ромб, трапеція;
ви дізналися :
про чотирикутники і його види;
ви навчилися:
• розпізнавати чотирикутник і його види (прямокутник, квадрат, паралелограм, ромб, трапеція);
•будувати вказані види чотирикутників та позначати їх літерами латинського алфавіту;
•виконувати необхідні вимірювання та обчислювати за формулою периметр (паралелограма, ромба, трапеції)

Часто виникає потреба порівняти, яка з частин площини є більшою, а яка - меншою Для цього вводять поняття площа многокутника (багатокутника)
Площа – це величина, яку можна не тільки порівнювати, а й вимірювати. За одиницю вимірювання площі приймають площу одиничного квадрата, тобто такого квадрата, сторона якого дорівнює одиниці довжини. Якщо, наприклад, сторона квадрата дорівнює 1 см, то його площа дорівнює 1 квадратному сантиметру (пишуть: 1 см2). Якщо сторона квадрата дорівнює 1 м, то його площа дорівнює 1 квадратному метру (1 м2).
 Визначити
площу фігури
— це
означає дізнатися, скільки
одиничних
квадратів уміщується
даній
фігурі.
Розглянемо
прямокутник АВСD,
у
якого довжина АD
= 4 см, а ширина АВ
=
3 см.
Визначити
площу фігури
— це
означає дізнатися, скільки
одиничних
квадратів уміщується
даній
фігурі.
Розглянемо
прямокутник АВСD,
у
якого довжина АD
= 4 см, а ширина АВ
=
3 см.
У ньому вміщується рівно 12 одиничних квадратів зі стороною 1 см (4 • 3 = 12). Отже, площа прямокутника АВСD дорівнює 12 см2.
Якщо довжина прямокутника дорівнює а м, а ширина - b м, то щоб знайти площу прямокут –
S = а • b
Це - формула площі прямокутника.
Слід пам'ятати, що коли а і b виражено в метрах, то площа S вимірюється у квадратних метрах. Коли а і b виражено в сантиметрах, то S - у квадратних сантиметрах і т. д.
Розгляньте таблицю одиниць вимірювання площі.
1 мм2 — площа квадрата, сторона якого 1 мм.
1 см2 — площа квадрата, сторона якого 1 см.
1 дм2 — площа квадрата, сторона якого 1 дм.
м2 — площа квадрата, сторона якого 1 м.
Ар (а) — площа квадрата, сторона якого 10 м (сотка).
Гектар (га) — площа квадрата, сторона якого 100 м.
1 км2 — площа квадрата, сторона якого 1 км.
Квадрат - це прямокутник, довжина якого а і ширина - а. Тому якщо сторона квадрата дорівнює а, то його площа
а
S = а 2
Ц е формула площі квадрата.
Площа паралелограма дорівнює добутку його сторони на висоту, проведену до цієї сторони.
S = a h
А висота паралелограма - це перпендикуляр, проведений із будь-якої точки однієї сторони до паралельної їй сторони.
 Площа
ромба
дорівнює половині добутку його діагоналей.
Площа
ромба
дорівнює половині добутку його діагоналей.
![]() AC,
BD-
діагоналі ромба.
AC,
BD-
діагоналі ромба.
![]() Площа
трикутника
дорівнює половині добутку його сторони
на висоту, проведену до цієї сторони. А
висота у трикутника – це перпендикуляр,
опущений з вершини трикутника на його
основу.
sABC=
ah
Площа
трикутника
дорівнює половині добутку його сторони
на висоту, проведену до цієї сторони. А
висота у трикутника – це перпендикуляр,
опущений з вершини трикутника на його
основу.
sABC=
ah

ВС=a , AH= h
Площа трапеції дорівнює добутку півсуми її основ на висотою.

Домовимося висотою трапеції , як і інших подібних фігур називати перпендикуляр, опущений з довільної точки основи трапеції на другу основу.
П еревір
себе:
еревір
себе:
Що таке одиничний квадрат?
Що означає визначити площу фігури?
За яким правилом знаходять площу прямокутника?
Напиши формулу площі: прямокутника; квадрата.
В яких одиницях виражають площі земельних ділянок?
Скільки арів і скільки квадратних метрів має гектар?
1.Знайдіть площу квадрата, сторона якого до- рівнює: 2 см; 3 дм; 9 м; 4 км.
2.Яку площу має прямокутник, якщо його сторони дорівнюють: 2 і 5 см; 3 і 10 дм ?
3.Скільки квадратних сантиметрів мас один: квадратний дециметр; квадратний метр?
4.Одна сторона прямокутника дорівнює 18 см, а друга - на 5 см довша. Знайди площу прямокутника.
5.Одна сторона прямокутника дорівнює 14 см, а друга - утричі довша. Знайди площу прямокутника.
6.Знайдіть площу квадрата, якщо його сторона
а = 8 см .
7.Знайдіть площу квадрата, периметр якого дорівнює 248 дм.
8 .Чому дорівнює периметр квадрата, якщо його площа становить 16 м2?
9.Є два квадрати. Сторона одного дорівнює 18м, а другого - 6 м. У скільки разів площа першого квадрата більша за площу другого?
10.Довжина і ширина аркуша паперу дорівнюють ЗО і 20 см. Знайдіть загальну площу такого паперу в пачці, що містить 200 аркушів.
11.Довжина і ширина кімнати дорівнюють 5 м і 3 м. Якою є площа кімнати?
12.Які з тверждень неправильні?
а) Якщо сторони прямокутника дорівнюють 4 і 10 см, то його площа становить 40 см2.
б) Якщо площа прямокутника дорівнює 40 см2, то його сторони - 4 і 10 см.
в) Якщо сторона квадрата дорівнює 6 см, то його площа - 36 см2.
г) Якщо площа квадрата дорівнює 36 см2, то його сторона - 6 см.
1 3.Знайдіть площу даного паралелограма.
14.Знайдіть площу трикутника, якщо відомо, що висота дорівнює 7 см , а сторона, до якої проведена висота, дорівнює 9 см.
15.Скільки квадратних міліметрів становить площа однієї клітинки твого зошита?
16.Обчисліть площі фігур, зображених на малюнку.


17.Знайдіть площу ромба, якщо його діагоналі дорівнюють 8 і 12 см.
18.Знайдіть площу трапеції, якщо її основи дорівнюють 6 і 8 см, а висота 4 см..
19. Виміряйте і обчисліть площу:
а ) обкладинки посібника;
б ) поверхні своєї парти.
20. Сторони одного прямокутника дорівнюють 15 і 13 см, а другого – 16 і 12 см . Площа якого прямокутника більша і на скільки?
21. Довжина класу дорівнює 8м, а ширина – 5 м. У класі навчається 20 учнів. Яка площа припадає на одного учня ?
22.Знайдіть площу даного трикутника.
23.Запишіть, скільки на малюнку трикутників.

24.Проведіть у трикутнику KLM відрізки так, щоб на малюнку їх стало 5.

25.Порахуйте, скільки на малюнку трикутників.

У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
площа;
одиниці вимірювання площі
ви навчилися :
виконувати необхідні вимірювання та обчислювати за формулою площу прямокутника, квадрата (паралелограма, ромба, трапеції);
обчислюти площу трикутника

У задачах на побудову потрібно будувати геометричні фігури за допомогою циркуля і лінійки.
За допомогою лінійки можна провести довільну пряму; пряму, що проходить через дану точку; пряму, що проходить через дві дані точки.
За допомогою циркуля, не змінюючи його розхилу, можна описати криву замкнену лінію, і дістанемо коло.

 Отже,
колом називається
замкнена плоска крива, всі точки якої
однаково віддалені від даної точки
(центра кола), що лежить у тій же площині,
що й крива.
Отже,
колом називається
замкнена плоска крива, всі точки якої
однаково віддалені від даної точки
(центра кола), що лежить у тій же площині,
що й крива.
Якщо вістря циркуля, яким накреслене коло, знаходилося в точці О, то ця точка - центр даного кола.
Відрізок, який сполучає будь-яку точку кола з його центром, називається радіусом кола.
Хорда — відрізок, який з'єднує будь-які дві точки кола.
Хорда, що проходить через центр кола, називається діаметром.
У колі можна провести безліч радіусів і безліч діаметрів.
Кожний діаметр кола у 2 рази довший за радіус.
Щоб виміряти довжину кола, можна вздовж нього покласти нитку і потім виміряти її довжину. А можна довжину кола не вимірювати, а обчислювати.
Вчені ще в давні часи виявили,що відношення довжини кожного кола до довжини його діаметра дорівнює одному й тому самому числу, наближене значення якого дорівнює 3,14. Це число в усьому світі позначають буквою π.
Отже, довжина кола l, обчислюється за формулою
l = 2 π r
![]()
Частина площини, обмежена колом, називається кругом .
Центром, радіусом, діаметром, хордою круга називають відповідно центр, радіус, діаметр, хорду кола, яке є межею даного круга.

Площа круга, як і довжина кола, залежить від довжини його радіуса.
S=πr²
Це - формула площі круга. Наприклад, якщо радіус круга дорівнює 10 см, то площа цього круга
S = 3,14 • 102; S =314(см2).
Частина круга, обмежена двома його радіусами, називається круговим сектором..
Область круга, обмежена хордою та дугою, називається сегментом.

Розглянемо найпростіші задачі на побудову.
 Побудова
трикутника з даними сторонами а,
Ь, с.
Побудова
трикутника з даними сторонами а,
Ь, с.

Для цього потрібно:
1. За допомогою лінійки проводимо довільну пряму і позначаємо на ній до вільну точку В.
На промені з початком В циркулем відкладаємо відрізок ВС — а.
Розхилом циркуля, що дорівнює b, описуємо коло з центром у точці С(на малюнку проводимо лише дугу кола).
Розхилом циркуля, що дорівнює с, описуємо коло з центром у точці В.
Точку А перетину цих кіл сполучаємо відрізками з точками В і С. Трикутник побудований.

Побудова кута, що дорівнює даному куту.

Для цього:
1. Проводимо промінь А,D.
2.Описуємо кола рівних радіусів з центрами А і А, Нехай одне коло перетинає сторони кута A у точках В і С, а друге — промінь А,D у точці В, .
3.Описуємо коло з центром В, , і радіусом ВС. Точка С, — точка перетину побудованих кіл.
4. Проводимо промінь A.C. Кут А , що дорівнює кутові А, побудований.


Побудова бісектриси даного кута
Для цього:
1. Описуємо коло довільного радіуса з центром у вершині А. Точки В і С — точки перетину кола зі сторонами кута.
Описуємо кола тим самим радіусом із центрів В і С. Точка О — точка перетину побудованих кіл.
Проводимо промінь АО. Це і є бісектриса кута.

Поділ даного відрізка навпіл

Для цього:
1. З точок А і В радіусом АВ описуємо кола. Точки С і D – точки перетину цих кіл.
 2.
Проводимо
відрізок СD.
Точка
О
— точка
перетину відрізків СD
і
АВ,
це і є середина відрізка АВ.
2.
Проводимо
відрізок СD.
Точка
О
— точка
перетину відрізків СD
і
АВ,
це і є середина відрізка АВ.
Побудова серединного перпендикуляра
 Через
точку О, яка належить прямій потрібно
провести пряму, перпендикулярну до
даної прямої а
Через
точку О, яка належить прямій потрібно
провести пряму, перпендикулярну до
даної прямої а
Для цього :
З даної точки О довільним радіусом проводимо коло. Точка А і В — точки перетину кола і прямої а.
З точок А і В проводимо кола радіусом АВ. Точка С — точка їх перетину.
3. Проводимо пряму СО.

П еревір себе:
За допомогою якого інструмента можна накреслити коло?
Що таке коло? Центр кола ? Радіус ? Діаметр ?
Що таке круг?
Як побудувати трикутник з даними сторонами?
Як побудувати кут, що дорівнює даному куту?
Як побудувати бісектрису даного кута?
Як поділити даний відрізок навпіл?
Як через дану точку провести пряму, перпендикулярну до даної прямої?
1.Побудуйте коло радіусом 3 см.
2.Побудуйте коло діаметром 8 см.
3.Накресліть довільний гострий кут. Потім побудуйте кут, що дорівнює даному.
4.Накресліть кут АВС 90°. Побудуйте бісектрису цього кута.
5.Побудуйте трикутник за трьома даними сторонами
АВ = 3см, ВС = 4 см, СА = 5 см.
6.Накресліть відрізок DK довжиною 3 см. Поділіть цей відрізок навпіл.
7.Проведіть пряму а і позначте на ній точку О.Через дану точку О проведіть пряму, перпендикулярну до прямої а.
8 .Накресліть трикутник АВС. Проведіть у ньому висоти.
9.Чому дорівнює довжина кола радіуса 1 см.?
10.Накресліть коло, радіус якого дорівнює 3 см. Позначте буквою його центр, проведіть радіус, діаметр.
11.Знайдіть радіус кола, діаметр якого дорівнює:
а ) 12 см;
в ) 22 см.
12.Побудуйте коло радіусом 4 см. Накресліть у ньому радіус, діаметр, хорду.
13.Побудуйте коло радіусом 5 см. Позначте у ньому сегмент, сектор.
14.Назвіть геометричні фігури, які використано для зображення курчати.

15. Яка фігура зайва? Обгрунтуйте свою відповідь.

У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
коло і круг;
центр, радіус, хорда, діаметр кола і круга;
довжина кола;
площа круга;
круговий сектор, сегмент
ви дізналися:
про користування креслярським приладдям (цир- кулем, олівцем, лінійкою, косинцем)
ви навчилися:
•будувати за допомогою циркуля коло, круг;
•будувати за допомогою циркуля і лінійки кут, рівний даному;
будувати за допомогою циркуля і лінійки серединний перпендикуляр; бісектрису кута, трикутник за трьома сторонами.
д ілити за допомогою циркуля і лінійки даний відрізок навпіл


На малюнку ви бачите предмети: циліндр, куб, куля, конус, паралелепіпед, піраміда. Усе це — геометричні тіла.

Геометричне тіло, поверхня якого складається із плоских многокутників, називається многогранником.
Поверхня многогранника складається з много -кутників, їх називають гранями; сторони многокутників — ребрами, а вершини — вершинами многогранника.

Уявіть куб, один із числа многогранників. Він має 6 граней, 12 ребер і 8 вершин . Кожна грань куба – квадрат, усі його ребра – рівні.

Фігурою, яка схожа на куб, але в якої не всі ребра рівні, і є прямокутний паралелепіпед .Усі його грані – прямокутники.
Отже, прямокутний паралелепіпед, має дві основи і чотири бічних грані.
Протилежні грані паралелепіпеда рівні і паралельні.
С ума площ усіх граней є площею поверхні прямокутного паралелепіпеда .
Бічна поверхня
S б = 2с (а + b).
Повна поверхня
S п = 2 (ac + bc + ab).
Об’єм прямокутного паралелепіпеда можна обчислювати подібно до того, як обчислюють площу прямокутника. За одиницю об'єму приймають об'єм одиничного куба. Якщо ребро куба дорівнює 1 м, то його об'єм — 1 кубічний метр (1 м3). Якщо ребро куба дорівнює 1 см, то його об'єм - 1 кубічний сантиметр (1 см3).
Для обчислення об'єму прямокутного паралелепіпеда , потрібна його довжина (а), ширина (b) і висота (с) . На нижню грань такого паралелепіпеда можна покласти аb кубиків з ребром 1 см. Оскільки висота прямокутного паралелепіпеда дорівнює с, то в нього можна вмістити таких кубиків у с разів більше, тобто аbс.

Отже, якщо виміри прямокутного паралелепіпеда а, b, с, то його об'єм
V = а b c
Це - формула об'єму прямокутного паралелепіпеда.
Об’єм куба обчислюється за формулою
V = а³,
оскільки
всі виміри рівні .
.
Призма
Призмою називається многогранник, який складається з двох рівних багатокутників, розміщених у паралельних площинах, вони є основами призми, і паралелограмів, вони є бічними гранями, число яких дорівнює числу сторін основи.

П лоща поверхні призми — це сума площ усіх її граней. Позначивши площу основи sосн, можна записати очевидну формулу для знаходження площі S поверхні призми:
S= Sбічн+2Sосн
Об’єм V даної призми обчислюють за формулою
V= Sосн h
де Sосн – площа основи призми, h – довжина бічного ребра.
Піраміда
Пірамідою називається многогранник, однією з граней якого є многокутник, вона називається основою піраміди, а інші грані, які називається бічними гранями -трикутники із спільною вершиною , яка називається вершиною піраміди.

Площа поверхні піраміди – це сума площ усіх його граней.
Перпендикуляр, опущений з вершини піраміди на площину її основи, називається висотою піраміди

 На
малюнку ви бачите трикутну піраміду
ABC, основа якої – трикутник і чотирикутну
піраміду ABCD, основа якої – чотирикутник.
На
малюнку ви бачите трикутну піраміду
ABC, основа якої – трикутник і чотирикутну
піраміду ABCD, основа якої – чотирикутник.
Об’єм V піраміди обчислюють за формулою
![]()
V= Sосн h
де sосн – площа основи піраміди,
h – довжина висоти піраміди
Циліндр
Циліндром називається геометрична фігура, що складається з двох кругів, які є паралельними, і всіх відрізків, що сполучають відповідні точки цих кругів. Круги називаються основами циліндра, а відрізки, що сполучають точки кіл кругів, твірними циліндра.

Радіусом циліндра називається радіус його основи.
Висотою циліндра називається відрізок, який сполучає його основи.
Відрізок ОО , який проходить через центри основ, називається віссю циліндра.
Р озрізавши поверхню циліндра по твірних, її можна розгорнути. В результаті утвориться розгортка поверхні циліндра.
 Бічна
поверхня циліндра розгортається в
прямокутник. Основа цього прямокутника
дорівнює довжині кола основи циліндра.
Бічна
поверхня циліндра розгортається в
прямокутник. Основа цього прямокутника
дорівнює довжині кола основи циліндра.
Якщо радіус основи циліндра дорівнює г, то довжина кола основи циліндра - 2πr. Тому основа прямокутника, в який розгортається бічна поверхня циліндра, також дорівнює 2πr. Висота h цього прямокутника - це висота даного циліндра. Площа розгортки бічної поверхні циліндра дорівнює 2πrh.
Така сама і площа бічної поверхні циліндра:
Sб = 2 πrh.
Щоб знайти площу всієї поверхні циліндра, треба до площі її бічної поверхні додати площу двох його основ. Оскільки площа круга радіуса r дорівнює πr², то площа поверхні циліндра
S= Sбічн+2Sосн
де S осн — площа основи циліндра
S = 2πrh + 2πr².
Об'єм V циліндра обчислюють за формулою
V= πr²h.




 де
r—
радіус основи циліндра, h—
довжина його твірної.
де
r—
радіус основи циліндра, h—
довжина його твірної.
Конус
 Конус
– це фігура, яка складається з круга –
це основа
конуса.
, точки, яка не лежить у площині цього
круга – це вершина
конуса
і всіх відрізків, що сполучають вершину
конуса з точками основи. Ці відрізки
називаються твірними
конуса.
Конус
– це фігура, яка складається з круга –
це основа
конуса.
, точки, яка не лежить у площині цього
круга – це вершина
конуса
і всіх відрізків, що сполучають вершину
конуса з точками основи. Ці відрізки
називаються твірними
конуса.
Пряму АС називають віссю конуса, відрізок АС — висотою конуса, точку А — вершиною конуса. Висота конуса перпендикулярна до площини його основи.
Якщо бічну поверхню конуса розрізати по одній з його твірних, а потім розгорнути її на площині, то отримаємо сектор. Радіус цього сектора дорівнює довжині l твірної конуса, а довжина дуги, яка обмежує сектор, — довжині кола, яке обмежує основу конуса.
Отриманий сектор називають розгорткою бічної поверхні конуса.
Площа бічної поверхні конуса S бічн дорівнює площі її розгортки
П оверхня
конуса складається з основи і бічної
поверхні.
оверхня
конуса складається з основи і бічної
поверхні.
Sбічн = πRl.
де R— радіус основи конуса, l — довжина його твірної.
Площа S поверхні конуса дорівнює сумі площі бічної поверхні і площі його основи:
S= Sбічн+2Sосн
де Sосн — площа основи конуса.
О б'єм V конуса обчислюють за формулою
V= πr²h
де r -радіус основи конуса, h – висота.
Сфера — це замкнена поверхня, що складається з усіх точок, однаково віддалених від однієї точки . Дану точку називають центром сфери.
Відрізок, який з'єднує центр сфери з точкою сфери називають радіусом сфери.
На малюнку точка О– центр сфери, R– радіус сфери.

Тіло, яке є частиною простору, обмеженою сферою, разом зі сферою, називають кулею. Сферу, яка обмежує кулю, називають також поверхнею кулі. Усі точки поверхні кулі однаково віддалені від центра кулі. Відрізок, який сполучає центр кулі з якою-не-будь точкою її поверхні, називається радіусом кулі. Відрізок, який сполучає дві точки поверхні кулі і проходить через її центр, - діаметром кулі. Діаметр кулі дорівнює двом її радіусам.
Площу S поверхні кулі, тобто сфери, обчислюють за формулою
S = 4πR²
де R— радіус кулі.
О![]() б'єм
V
кулі
обчислюють за формулою
б'єм
V
кулі
обчислюють за формулою
де ОА — радіус кулі.

Перевір себе:
 Назви елементи
куба.
Назви елементи
куба.
Що таке прямокутний паралелепіпед?
Назви елементи прямокутного паралелепіпеда?
Що таке піраміда?
Поясніть, що таке циліндр.
Поясніть, що називають основами, бічною поверхнею і твірними циліндра.
Яка геометрична фігура є розгорткою бічної поверхні циліндра?
Поясніть, що таке конус .
Поясніть, що називають основою, бічною
поверхнею і твірними конуса.
Я ка геометрична фігура є розгорткою бічної поверхні конуса?
Яку фігуру називають сферою?
Що називають центром сфери?
Що називають радіусом сфери?
Яку фігуру називають кулею?
Що називають поверхнею кулі?
Що таке одиничний куб? Чому дорівнює його
об'єм?
За якою формулою обчислюють:
об'єм прямокутного паралелепіпеда;
об'єм куба?
1.Знайдіть об'єм куба, якщо площа однієї його грані дорівнює 9 см2.
2.Скільки ребер має куб? А вершин?
3.Ребро куба дорівнює 2 см. Знайди:
а) суму довжин усіх його ребер;
б) площу однієї грані куба;
в) суму площ усіх граней куба;
г) об'єм куба.
4.Ребра прямокутного паралелепіпеда дорівнюють 1, 2 і 3 см. Знайдіть:
а) його об'єм;
б) площу його найменшої грані;
в) площу найбільшої грані .
5.Зобразіть у зошиті куб.
6.Намалюйте прямокутний паралелепіпед. Позначте його вершини буквами.
7 .Практичне завдання.
Зробивши потрібні вимірювання, обчисліть об'єм:
а) сірникової коробки;
б) своєї кімнати.
8
 .
Порахуйте, скільки одиничних кубів
вміщується у цих фігурах
.
Порахуйте, скільки одиничних кубів
вміщується у цих фігурах
9.Знайдіть об’єм кулі, якщо радіус дорівнює 3 см.
10.Знайдіть площу поверхні кулі, якщо радіус дорівнює 2 см.
11.Знайдіть об’єм конуса, якщо радіус його основи дорівнює 2см, а висота конуса – 4 см.
12.Знайдіть об’єм призми, якщо площа його основи 36см2, а довжина бічного ребра – 5 см
13.Знайдіть об’єм піраміди, якщо площа його основи дорівнює 40 см2, а висота піраміди – 8 см.
У ЦЬОМУ ПАРАГРАФІ :
було введено такі поняття:
прямокутний паралелепіпед (вершини, грані, ребра, основа, висота);
призма (вершини, грані, ребра, основа);
піраміда (вершина, грані, ребра, основа, висота); циліндр (бічна поверхня, основа, висота);
конус (вершина, основа, висота);
куля, сфера (центр, радіус)
ви дізналися:
про просторові фігури та їхні складові
ви навчилися:
розпізнавати та називати просторові фігури, показувати їх на моделях;
•вимірювати та обчислювати за формулою площі поверхонь та об'єм и
Цікавий матеріал
Зустріч із точкою
Одного разу лежав Олівець самотньо у пеналі й сумував. Його друзі — олівці у різнокольорових яскравих сорочечках були в іншій коробці. Вони хизувалися тим, що дівчинка Тетянка часто брала їх у руки, малювала ними сонечко, барвистих метеликів, квіти. Олівець лежав у пеналі й думав, що він нікому не потрібний, що він негарний, він — ніякий, він — простий олівець.
Та якось він викотився з пеналу, та його гострий носик торкнувся аркуша паперу. На папері Олівець побачив слід від свого носика й зрадів: «Я намалював крапку!» Аж тут крапка ожила й вигукнула: «Неправда! Я не просто крапка. Я — Точка! Найголовніша в геометрії. А ти, Олівчику, мій найкращий друг і в геометрії всім необхідний».
Олівець від радості ще постукав носиком і поставив кілька точок.
— А вам, діти, подобається ставити точки? Спробуйте їх поставити так, як це зробив Олівець.
Знайомство з лінією
Простому Олівцю дуже подобалось ставити точки. Коли точки на його малюнку вишикувались пліч-о-пліч, то утворилась лінія.
Спробуйте і ви, діти, за допомогою точок накреслити лінію. Отже, лінія — це багато точок (множина точок). Олівець подумав, поставив дві точки, а потім їх з'єднав. Вийшла така лінія
а![]() потім вийшло так:
потім вийшло так:
і
о![]() сь
так:
сь
так:
Він зрозумів тепер, що через 2 точки можна провести багато різних ліній.
![]()
— А ви, діти, із ліній утворіть ось такі орнаменти:

Тощо
Допомога лінійки
(Пряма лінія. Відрізок. Промінь)
Олівець захопився кресленням ліній. Кожна наступна виходила у нього рівнішою. Лінійка довго спостерігала за Олівцем, а потім запропонувала йому свою допомогу. Олівець провів носиком уздовж лінійки по аркушу паперу і у нього вийшла пряма лінія. Потім він хотів порахувати, скільки прямих ліній можна провести через одну точку. Він креслив, рахував, але так і не дізнався, скільки прямих проходить через одну точку.

А як ви думаєте, скільки?
Олівець вирішив провести багато прямих ліній через дві точки.
— Спробуйте і ви це зробити. Що у вас вийшло?
і в Олівця теж нічого не вийшло. Лінійка його заспокоїла й сказала, що через дві точки можна провести тільки одну пряму.
Маленькій Точці сподобалась пряма лінія. Вона вийшла на пряму лінію і пішла по ній. Ішла довго. Стомилась. Зупинилась і каже: «Чи довго ще я буду йти? Чи швидко кінець прямої лінії?»
Засміялась Пряма: «Ох ти, Точко! Ти не дійдеш до кінця. Хіба ти не знаєш, що у прямої немає кінця?!»
Т оді я поверну назад, — сказала Точка, —. я, мабуть, пішла не в той бік.
І у другу сторону не буде кінця. У прямої лінії зовсім немає кінців. Якщо ти не хочеш іти без кінця, то давай покличемо на допомогу Ножиці.
І справді, з'явилися Ножиці. Вони весело клацнули і розрізали пряму.
— Ура! — закричала Точка, — от і кінець з'явився. Молодці, Ножиці! А тепер, будь ласка, зробіть кінець і з іншого боку.
Ножиці знову клацнули.
Ой, як цікаво! — вигукнула Точка. — Що ж це з моєю прямою сталося? З одного боку — кінець, а з іншого — теж кінець. Як це називається?
Це відрізок, — сказали Ножиці, — ти, Точко, стоїш на відрізку прямої.
_________ ___________ __________
М ені відрізок подобається. Але шкода прямої. Що з неї ще залишилося? Теж відрізки?
Н і, — відповіли Ножиці, — у них тільки з одного боку є кінець, а в інший бік немає кінця. І називаються вони променями. Це промені.
Ах! — радісно сказала Точка, — я знаю, чому вони так називаються. Вони схожі на сонячні промені. Сонячні промені на сонці починаються та йдуть від сонця без кінця.
