вопросы промежуточной аттестации
ВОПРОСЫ к зачету (1-й семестр)
по курсу « математика» для студентов 1-го курса зооинженерного факультета по направлению 36.03.02“Зоотехния” профили: Кинология»,
«Технология производства продукции скотоводства»
Матрицы. Операции над матрицами.
Определители. Вычисление определителей
Ранг матрицы
Обратная матрица.
Системы линейных уравнений
Метод Крамера
Метод Гаусса.
Векторы. Линейные операции над ними. Разложение векторов.
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов.
Метод координат на плоскости
Прямая на плоскости.
Математические модели. Множества. Функции и их графики
Последовательности. Предел числовой последовательности
Предел функции. Непрерывность функции
Методы вычисления пределов
Производная функции. Геометрический смысл производной
Исследование функций и построение графиков. Выпуклость функции
Использование понятия производной в задачах с.-х. производства
Производная и дифференциал функции. Приближенное вычисление с помощью дифференциала
Важнейшие свойства и основные методы интегрирования неопределенных интегралов
Интегрирование рациональных дробей
Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов.
Несобственные интегралы
Приложения определенного интеграла.
Применение определенного интеграла к решению задач с.-х. производства.
Численные методы. Формула Симпсона.
Вопросы к экзамену
по курсу « математика» для студентов 1-го курса
зооинженерного факультета по направлению 36.03.02 «Зоотехния» профили: «Кинология», «Технология производства продукции скотоводства»
Матрицы. Операции над матрицами.
Определители. Вычисление определителей
Ранг матрицы
Обратная матрица.
Системы линейных уравнений
Метод Крамера
Метод Гаусса
Векторы. Линейные операции над ними. Разложение векторов
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Метод координат на плоскости.
Прямая на плоскости.
Математические модели. Множества. Функции и их графики
Последовательности. Предел числовой последовательности
Предел функции. Непрерывность функции
Методы вычисления пределов
Производная функции. Геометрический смысл производной
Исследование функций и построение графиков. Выпуклость функции
Использование понятия производной в задачах с.-х. производства
Производная и дифференциал функции. Приближенное вычисление с помощью дифференциала.
Важнейшие свойства и основные методы интегрирования неопределенных интегралов
Интегрирование рациональных дробей.
Определенный интеграл, основные свойства. Методы и приемы вычисления определенных интегралов.
Несобственные интегралы.
Приложения определенного интеграла Применение определенного интеграла к решению задач с.-х. производства.
Численные методы. Формула Симпсона.
Числовые ряды. Признаки сходимости.
Степенные ряды. Ряды Тейлора и Маклорена
Функции двух переменных. Частные производные функции двух переменных
Экстремум функции двух переменных
Функции нескольких переменных. Градиент функции 2-х переменных
Метод наименьших квадратов
Дифференциальные уравнения 1-го порядка с разделяющимися неизвестными
Линейные дифференциальные уравнения 1-го порядка
Использование дифференциальных уравнений 1-го порядка в задачах с.-х. производства.
Классическое и статистическое определение вероятности случайного события
Элементы комбинаторики
Теоремы сложения и умножения вероятностей
Формула полной вероятности. Формула Байеса.
Дискретная случайная величина. Законы распределения
Дискретная случайная величина. Числовые характеристики
Повторные испытания. Формула Бернулли
Локальная и интегральная теоремы Лапласа
Законы распределения. Распределение Пуассона.
Дискретная случайная величина. Понятие наивероятнейшего числа испытаний
Закон больших чисел в формуле Чебышева
Нормальное распределение непрерывной случайной величины
Правило трёх сигм
Равномерное и показательное распределения непрерывной случайной величины
Генеральная совокупность и выборка. Понятие выборочной оценки генеральной совокупности.
Вариационный ряд. Гистограмма
Точечные выборочные оценки и их свойства. Несмещённые оценки. Средняя квадратичная ошибка выборки.
Доверительный интервал. Доверительный интервал для дисперсии.
Доверительный интервал для среднего значения нормального распределения.
56.Понятие корреляционного анализа. Построение прямой линии регрессии на основе метода наименьших квадратов.
57.Линейная регрессия со сгруппированными данными
58.Линейная регрессия с несгруппированными данными в технологиях продуктов скотоводства.
59. Дисперсионный анализ в технологиях продуктов скотоводства.
Задачи для экзамена
1. Найдите матрицу С-1, обратную к матрице С = АВ’ + 3Е:
а)
А =
В=
2.По формулам Крамера решить систему:
а)
б)
3. Решить матричные уравнения:
а)
б)
4
.
Даны два единичных вектора m
и n,
угол между которыми 120
.
Найти:
а)
острый угол между диагоналями
параллелограмма построенного на векторах
и
;
б) проекцию вектора на направление вектора
а) =2m-n,
= -3m+n
б) =7m-3n,
= -m+2n
3.Дана
пирамида с вершинами в точках:а)
б)
Найти:
а)
длину ребра
,
б) объем пирамиды
в) площадь основания и высоту пирамиды,
5.
Даны четыре вектора a1,
a2,
a3
и b
в некотором базисе. Показать, что
векторы
,
,
:
образуют базис, и найти координаты вектора b в этом базисе:
а) =(3;-5;2)
=(4;5;1)
=(-3;0;-4)
b=(-4;5;-16)
б) =(2;1;3)
=(3;-2;1)
=(1;-3;-4)
b=(3;0;1)
11. Найти собственные значения и собственные векторы матрицы А . Привести к
диагональному виду матрицу А.
А=
А=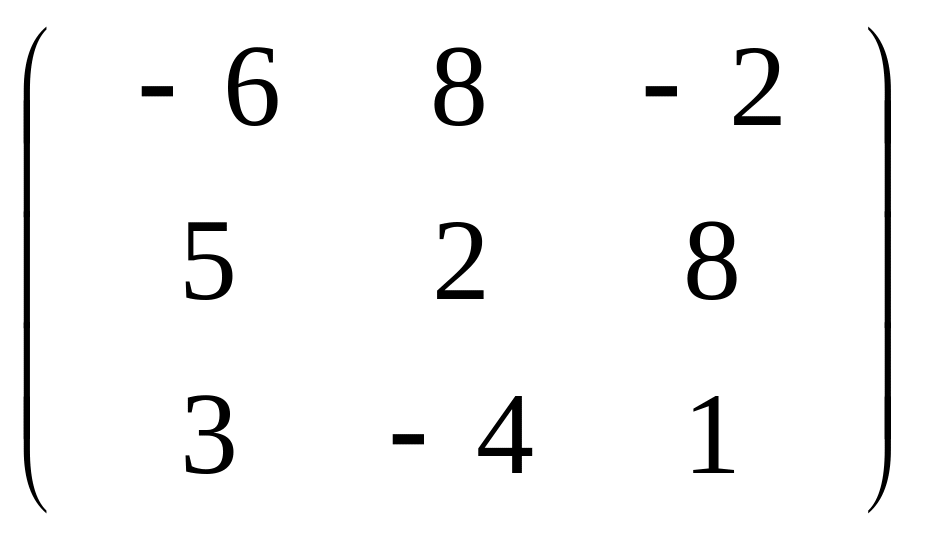
6.Найти область определения функций:
:
7.Выяснить четность (нечетность) функций:
8. Вычислить предел:
а)
б)
9.Найти производные функций:
а)Y=(2-x)l
n(
+5x)
б)Y=arctg
10. Найти производную n-го порядка:
а)
б)
y=
11. Составить уравнения касательных к графику функции:
а)
проходящих через точку М(2;-2)
б)
y=
проходящих через точку М(4;-4)
12.Построить график функций:
а)
y=x
y=
б)y=x
y=
13.Вычислить приближенно с помощью дифференциала:
а)
б)
14.а)На
сколько процентов увеличится у=
, если x увеличится на :
2 %
б)На сколько процентов увеличится у= , если x увеличится на :
4%
15.Вычислить неопределенный интеграл:
а)
б)
16. Вычислить определенные интегралы:
а)
б)
17. а) Найти площадь фигуры ограниченной линиями:
б) Найти площадь фигуры ограниченной линиями:
y=x
y=x+3
18.Вычислить несобственный интеграл (если он сходится):
а)
б)
19.Исследовать сходимость рядов:
а)
б)
20.Разложить в степенной ряд по степени х функции:
а)у
= е
б)у
= sin
21. Разложить в степенной ряд функции:
а) Y= lnx по степеням (x-1)
б) y= x4+ x2 по степеням (x-1)
22. Применяя почленное интегрирование или дифференцирование рядов найти их суммы:
а)x-
-
+
x
б)1+2x+3x2+4x3+
x
23. Исследовать на экстремум функцию z=f (x,y)
а)
z=3x+3y-x
-xy-y
+6
б)z=7x+8y-x -xy-y -10
24. Найти частные производные функции:
а)
z=e
б)
z=xe
25. Исследовать функции на условный экстремум:
1)Z=x2+y2-xy+x+y-4 при x+y+3=0
2)Z=2x+y при x2+y2=5
26. Вычислить с точностью до 0,01 корень уравнения x3-2x2 -4x-7=0, содержащийся в промежутке (3;4) способом хорд.
27.Определить
максимальное значение функции f=2x+4y-
x2-2 y2
при условиях:
28.Найти максимальное значение функции F=- x -y
при
условиях (x-7)
+(y-7)
18
x
;y
0
29. Решить уравнение 2x =4x
30. а) В первом ящике 6 шаров: 1 белый,3 красных и 2 синих. Во втором ящике 12 шаров: 2 белых, 6 красных, 4 синих. Из каждого ящика вынули по шару. Найти вероятность того, что среди них нет синего шара.
б) Из заготовленной для посева пшеницы зерно первого сорта составляет 40%, второго сорта-50%,третьего сорта-10%. Вероятность того, что взйдет зерно первого сорта равна 0,8 ,второго-0,5 , третьего-0,3 . Найти вероятность того ,что взойдет наугад взятое зерно.
31. а) Событие В наступает в том случае, если событие А появится не менее трех раз. Определить вероятность появления события В, если вероятность появления события А при одном опыте равна 0,4 и произведено 4 независимых опыта.
б)Вероятность падания в цель при одном выстреле равна 0,8. написать закон распределения вероятностей попаданий в цель пи 5 выстрелах .
32. а) Бросаются три игральные одинаковые кости. Найти вероятность того, что хотя бы на одной кости выпадет 6 очков.
б)Самолет сбрасывает 4 авиационные бомбы. Вероятность попадания 0,75 .Найти вероятность попадания хотя бы одной бомбы.
33. а) Норма высева семян на 1 га равно 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим отклонением 10 кг. Определить количество семян, обеспечивающих посев на площади 100 га с гарантией 0,95.
б)Всхожесть семян пшеницы составляет 90%. Определить наиболее вероятное число всходов из 200 посеянных семян.
34. а) Масса яблока, средняя величины которой равна 150 г, является нормально распределенной случайной величиной со средним квадратическим отклонением 20 г. Найти вероятность того, что масса наугад взятого яблока будет заключена в пределах от 130 г до 180 г.
б) Средний вес зерна составляет 0,2 г., среднеквадратическое отклонение равно 0,05 г. Определить вероятность того ,что вес наудачу взятого зерна окажется в пределах от 0,16г. до 0,22г.
35.Случайная величина Х задана интегральной функцией распределения F(х). найти : 1)дифференциальную функцию распределения f(х); 2) математическое ожидание М(Х); 3)дисперсию D(Х).
X -4 -3 -2 0 1
P 0,1 0,1 0,5 0,2 0,1
X 50 48 51 53
P 0,3 0,2 0,2 0,3
36.
Заданы результаты обследования.
Требуется: 1)получить вариационный ряд
и построить гистограмму относительных
частот; 2)вычислить выборочную среднюю
,
дисперсию
,
среднее квадратичное отклонение s
, коэффициент вариации v
, ошибку средней s
; 3) с надежностью 95% указать доверительный
интервал для оценки генеральной
средней
.
Обследованию по весу (кг.) 15кроликов. Результаты обследования представлены в таблице
№наблюдения 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
а) 3,1 4,2 5,0 4,6 6,4 5,3 3,8 5,1 4,9 5,4 5,4 5,9 4,9 4,7 4,8
б) 5,.5 4,8 4,9 4,5 5,7 5,3 5,2 4,7 4,8 4,9 5,1 5,0 4,7 4,3 4,6
37. Приводятся данные о весе зерна в мг. (X) и процентным содержанием жира в нем (y). Вычислить коэффициент корреляции и найти выборочное уравнение прямой регрессии Y на X.
а)
X 35 40 45 48 49 47 45 40 36 35
Y 4 5 6 7 7 6 8 8 4 5
б)
X 38 41 44 45 50 51 49 40 39 33
Y 3 9 8 5 5 7 6 9 4 4
Приводятся данные об урожайности и площади . Вычислить коэффициент корреляции и найти выборочное уравнение прямой регрессии У на Х
Урожайность, ц/га |
10 -12 |
12 -14 |
14 -16 |
16 -18 |
18 -20 |
20 -22 |
22 -24 |
Площадь, га |
5 |
11 |
17 |
14 |
22 |
11 |
20 |
38.
Проведено по пять испытаний на
каждом из четырех уровней фактора
Ф. Результаты испытаний приведены в
таблице. Методом дисперсионного
анализа при уровне значимости
проверить нулевую гипотезу о равенстве
групповых средних.
а)
Номер измерения |
Уровни фактора |
||
Ф |
Ф |
Ф |
|
1 |
10 |
17 |
14 |
2 |
15 |
15 |
18 |
3 |
14 |
25 |
30 |
4 |
18 |
22 |
27 |
5 |
20 |
30 |
34 |
6 |
16 |
28 |
40 |
б) Проведено по пять испытаний на каждом из четырех уровней фактора Ф. Результаты испытаний приведены в таблице. Методом дисперсионного анализа при уровне значимости проверить нулевую гипотезу о равенстве групповых средних.
Номер измерения |
Уровни фактора |
|||
Ф |
Ф |
Ф |
Ф |
|
1 |
36 |
56 |
52 |
39 |
2 |
47 |
61 |
57 |
57 |
3 |
50 |
64 |
59 |
63 |
4 |
58 |
66 |
58 |
61 |
5 |
67 |
66 |
79 |
65 |
1. а) В первом ящике 6 шаров: 1 белый,3 красных и 2 синих. Во втором ящике 12 шаров: 2 белых, 6 красных, 4 синих. Из каждого ящика вынули по шару. Найти вероятность того, что среди них нет синего шара.
б) Из заготовленной для посева пшеницы зерно первого сорта составляет 40%, второго сорта-50%,третьего сорта-10%. Вероятность того, что взйдет зерно первого сорта равна 0,8 ,второго-0,5 , третьего-0,3 . Найти вероятность того ,что взойдет наугад взятое зерно.
2. а) Событие В наступает в том случае, если событие А появится не менее трех раз. Определить вероятность появления события В, если вероятность появления события А при одном опыте равна 0,4 и произведено 4 независимых опыта.
б)Вероятность падания в цель при одном выстреле равна 0,8. написать закон распределения вероятностей попаданий в цель пи 5 выстрелах .
3. а) Бросаются три игральные одинаковые кости. Найти вероятность того, что хотя бы на одной кости выпадет 6 очков.
б)Самолет сбрасывает 4 авиационные бомбы. Вероятность попадания 0,75 .Найти вероятность попадания хотя бы одной бомбы.
4. а) Норма высева семян на 1 га равно 200 кг. Фактический расход семян на 1 га колеблется около этого значения со средним квадратическим отклонением 10 кг. Определить количество семян, обеспечивающих посев на площади 100 га с гарантией 0,95.
б)Всхожесть семян пшеницы составляет 90%. Определить наиболее вероятное число всходов из 200 посеянных семян.
Индивидуальные творческие задания (проекты):
1 Тема Корреляционный анализ
112.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
3 |
3 |
8 |
15 |
9 |
22 |
40 |
113.
Урожайность, ц/га |
10 - 12 |
12 - 14 |
14 - 16 |
16 - 18 |
18 - 20 |
20 - 22 |
22 - 24 |
Площадь, га |
8 |
2 |
5 |
7 |
11 |
29 |
38 |
114.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
10 |
11 |
13 |
17 |
5 |
22 |
22 |
115.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
5 |
13 |
15 |
17 |
12 |
20 |
18 |
116.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
5 |
9 |
14 |
15 |
27 |
20 |
10 |
117.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
3 |
4 |
3 |
10 |
20 |
30 |
30 |
118.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
3 |
4 |
7 |
10 |
16 |
22 |
38 |
119.
Урожайность, ц/га |
10 - 12 |
12 - 14 |
14 - 16 |
16 - 18 |
18 - 20 |
20 - 22 |
22 - 24 |
Площадь, га |
2 |
2 |
6 |
11 |
21 |
29 |
29 |
120.
Урожайность, ц/га |
11 - 13 |
13 - 15 |
15 - 17 |
17 - 19 |
19 - 21 |
21 - 23 |
23 - 25 |
Площадь, га |
6 |
10 |
8 |
18 |
28 |
22 |
8 |
Критерии оценки:
оценка «отлично» выставляется студенту, если выполнено верно индивидуальное задание и все задания групповой работы;
оценка «хорошо» выставляется студенту, если выполнено верно индивидуальное задание и все задания групповой работы. Но они вызывают сложность при воспроизведении решения во время опроса;
оценка «удовлетворительно» если верно выполнены все задания, но в задании индивидуального плана допущены неточности в вычислениях.
оценка «неудовлетворительно», если не верно выполнены некоторые задания, но в задании индивидуального плана допущены неточности в вычислениях.
-
оценка «зачтено» выставляется студенту,
если студентом не получена оценка
«неудовлетворительно».
-
оценка «не зачтено» ,если была получена
оценка «неудовлетворительно».
Составитель
________________________ И.С. Жукова
(подпись)
«_25__»_января________________20
16 г.