19. Кинетическая энергия вращающегося тела. Работа внешних сил при вращении твердого тела вокруг неподвижной оси. Кинетическая энергия твердого тела при плоском вращении.

Если тело вращается вокруг неподвижной оси с угловой скоростью ω, то линейная скорость i-ой точки равна  , где  , - расстояние от этой точки до оси вращения. Следовательно,

где J - момент инерции тела относительно оси вращения. При вращении твёрдого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:

dA = dE или 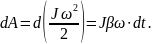 Учитывая, что Jβ=M, ωdr=dφ, имеем При вращении твёрдого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси. Если момент сил относительно оси равен нулю, то эти силы работы не производят. Кинетическая энергия твёрдого тела при его плоском движении равна сумме 2-х слагаемых:

E_кин = m v₀² / 2 + J₀ w² / 2, где m – инертная масса тела, v₀ – скорость поступательного движения центра масс тела, J₀ - момент инерции тела относительно центральной оси, w - угловая скорость вращения тела относительно этой оси.

20. Закон Кулона. Напряженность электростатического поля точечного заряда. Принцип суперпозиции. Графическое изображение электростатического поля. Силовые линии однородного и неоднородного поля. Свойства линий силового поля.

Закон Кулона — это закон, описывающий силы взаимодействия между неподвижными точечными электрическими зарядами: Силы взаимодействия между неподвижными зарядами прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между этими зарядами.

Н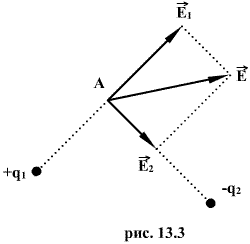 апряженность электростатического поля в данной точке есть физическая величина, определяемая силой, которая действует на пробный единичный положительный заряд, помещенный в эту точку поля: 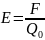 . Как следует из формулы и закона Кулона, напряженность поля точечного заряда в вакууме 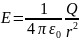 , где 1/4пЕ₀=k=>E=kQ/r² k=9*10⁹ Направление вектора Е совпадает с направлением силы, которая действует на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду. Если поле образовано не одним зарядом, а несколькими, то силы, действующие на пробный заряд, складываются по правилу сложения векторов. Поэтому и напряженность системы зарядов в данной точке, поля равна векторной сумме напряженностей полей от каждого заряда в отдельности.

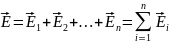
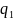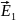С огласно принципу суперпозиции электрических полей можно найти напряженность в любой точке А поля двух точечных зарядов   и  . Сложение векторов   и   производится по правилу параллелограмма. Направление результирующего вектора 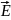  находится построением, а его абсолютная величина может быть подсчитана по формуле:

Для графического изображения электростатических полей используют линии вектора E (или силовые линии) - они проводятся так, чтобы в каждой точке вектор был направлен по касательной к ним. Линии вектора E нигде не пересекаются, они начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность. В случае однородного поля в каждой точке которого вектор одинаков и по модулю, и по направлению, линии представляют собой прямые, параллельные друг другу и отстоящие друг от друга на одинаковом расстоянии.

Обычно линии проводят так, чтобы их густота в каждой точке поля определяла числовое значение вектора E. Под густотой линий понимают количество линий, пронизывающих перпендикулярную к ним плоскую поверхность фиксированной площади.

Свойства силовых линий:

· Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных.

· Силовые линии электрического поля всегда перпендикулярны поверхности проводника.

· Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным (если силовые линии параллельны) и неоднородным (если силовые линии не параллельны).

21. Потенциал электрического поля. Потенциал точечного заряда. Соотношение, связывающее напряженность поля и потенциал. Графическое изображение электростатического поля. Силовые линии и эквипотенциальные поверхности.

Потенциал электрического поля - это энергетическая характеристика поля. Он представляет собой работу, которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд, находящийся на бесконечности в данную точку поля. Измеряется потенциал электрического поля в вольтах. В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.

Потенциал электростатического поля в точке r равен отношению потенциальной энергии пробного точечного заряда q', помещенного в данную точку, к величине этого заряда q'. .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала. E = - grad ф 

По осям координат: Направление силовой линии (линии напряженности) в каждой точке совпадает с направлением  .Отсюда следует, что напряженность   равна разности потенциалов U на единицу длины силовой линии. Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определить  между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить    наиболее просто: 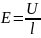. Теперь дадим определение эквипотенциальной поверхности. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности При перемещении по этой поверхности на dl потенциал не изменится: dφ=0. Отсюда следует, что проекция вектора   на dl равна нулю, то есть  Следовательно,   в каждой точке направлена по нормали к эквипотенциальной поверхности.