34. Магнитное поле кругового тока. Магнитное поле в центре кругового тока.

Как следует из рисунка, все элементы кругового тока создают в центре магнитные поля одинакового направления - вдоль нормали от витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то

Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током

35. Магнитное поле прямого бесконечного проводника с током.

Магнитное поле прямого тока - тока, текущего по тонкому прямому проводу бесконечной длины

В произвольной точке А, удаленной от оси проводника на расстояние R, векторы от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа ("к нам"). Поэтому сложение векторов можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол 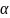(угол между векторами и ), выразив через него все остальные величины. Из рис. следует, что

,

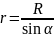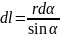
(радиус дуги CD вследствие малости равен r, поэтому угол FDC можно считать прямым). Подставив эти выражения, получим, что магнитная индукция, создаваемая одним элементом проводника, равна

Так как угол для всех элементов прямого тока изменяется в пределах от 0 д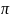о , то

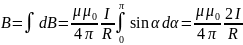
Следовательно, магнитная индукция поля прямого тока

36. Сила Ампера. Взаимодействие параллельных проводников с током.

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, А. Ампер установил, что сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, равна 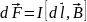, где - вектор, по модулю равный и совпадающий по направлению с током, 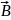- вектор магнитной индукции. Направление вектора может быть найдено, согласно , по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор  , а четыре вытянутых пальца — по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера вычисляется по формуле 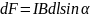, где - угол между векторами и .

Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока 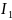 и (на рис. токи направлены перпендикулярно плоскости чертежа к нам), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током.

Рассмотрим, с какой силой действует магнитное поле тока   на элемент второго проводника с током . Ток  создает вокруг себя магнитное поле, линии индукции которого представляют собой концентрические окружности. Направление вектора определяется правилом правого винта, его модуль равен .

Направление силы  с которой поле  действует на участок  второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, с учетом того, что угол  между элементами тока  и вектором  прямой, равен . Подставляя значение для  получим . Рассуждая аналогично, можно показать, что сила 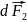,c которой магнитное поле тока   действует на элемент  первого проводника с током направлена в противоположную сторону и по модулю равна . Сравнение выражений и показывает, что , т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой . Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания.