28. Теорема Гаусса для электростатического поля в вакууме. Расчет поля равномерно заряженного по объему шара с известной объемной плотностью заряда

Т еорема Гаусса для электростатического поля в вакууме см. вопрос 25!

Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ=dQ/dV — заряд, приходящийся на единицу объема). Учиты­вая соображения симметрии, можно показать, что для напряженности поля вне ша­ра получится тот же результат, что и в предыду­щем случае: E=  . Внутри же шара на­пряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q’=4/3πr’³ρ.                           

Поэтому, согласно теореме Гаусса, 4πr’²E=Q’/ε₀=4/3πr³ρ/ε₀. Учитывая, что ρ=Q/(4/3πR³)

получим: E=  Таким образом, напряженность ноля вне равно­мерно заряженного шара описывается форму­лой: E=  , а внутри его изменяется линейно с расстоянием r' согласно выражению. График зависимости E от r:

29. Энергия электрического поля и ее локализация в пространстве. Выразить энергию заряженного конденсатора через напряженность конденсатора.

Взаимодействие зарядов осуществляется посредством поля, которое, как материальный объект, должно обладать энергией.

В плоском конденсаторе, если пренебречь краевыми эффектами, однородное электрическое поле сосредоточено в пространстве между пластинами. Выразим энергию конденсатора через напряженность поля, используя формулы: 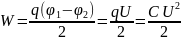; U=Ed; C=ε₀εS/d.

Тогда: , где V=Sd - объем пространства, в котором сосредоточено электрическое поле конденсатора (пренебрегая краевыми эффектами). В этом случае величина 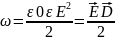  представляет собой объемную плотность энергии электрического поля.

Важно отметить, что это свидетельствует о локализации энергии в пространстве, в котором существует электрическое поле.

Действительно, эксперименты, особенно с переменными во времени полями, которые могут существовать независимо от зарядов и распространяться в пространстве, показывают, что носителем энергии является поле.

30. Магнитное поле. Магнитная индукция. Силовые линии магнитного поля. Сила Лоренца.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты). Кроме этого, оно возникает в результате изменения во времени электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции B {\displaystyle \mathbf {B} }(вектор индукции магнитного поля. С математической точки зрения {\displaystyle \mathbf {B} =\mathbf {B} (x,y,z)}B=B(x;y;z) — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина). Магнитное поле, как и электростатическое, удобно представлять в графической форме – с помощью силовых линий магнитного поля.

Силовая линия магнитного поля – это линия, касательная к которой в каждой точке совпадает с направлением вектора магнитной индукции. Силовые линии магнитного поля проводят так, что их густота пропорциональна величине магнитной индукции: чем больше магнитная индукция в некоторой точке, тем больше густота силовых линий.

Таким образом, силовые линии магнитного поля имеют сходство с силовыми линиями электростатического поля.

Однако им свойственны и некоторые особенности. Рассмотрим магнитное поле, созданное прямым проводником с током I. Пусть этот проводник перпендикулярен плоскости рисунка. В различных точках, расположенных на одинаковых расстояниях от проводника, индукция одинакова по величине. Линией, касательная к которой во всех точках совпадает с направлением вектора магнитной индукции, является окружность. Следовательно, силовые линии магнитного поля в этом случае представляют собой окружности, охватывающие проводник. Центры всех силовых линий расположены на проводнике.

Таким образом, силовые линии магнитного поля замкнуты (силовые линии электростатического не могут быть замкнуты, они начинаются и заканчиваются на зарядах). Поэтому магнитное поле является вихревым (так называют поля, силовые линии которых замкнуты). Замкнутость силовых линий означает ещё одну, очень важную особенность магнитного поля – в природе не существует (по крайней мере, пока не обнаружено) магнитных зарядов, которые являлись бы источником магнитного поля определённой полярности. Поэтому не бывает отдельно существующего северного или южного магнитного полюса магнита. Даже если распилить пополам постоянный магнит, то получится два магнита, каждый из которых имеет оба полюса. На заряд, движущийся в магнитном поле, действует сила. Эту силу принято называть силой Лоренца.

F_л=qvBsinα, где – угол между векторами v иB. Направление силы Лоренца зависит от направления вектора [v, B]. Его можно определить с помощью правила правого винта или правила левой руки. Но направление силы Лоренца не обязательно совпадает с направлением вектора.

Если заряд положительный, то F_л параллельна вектору [v, В]. Если же q < 0, то сила Лоренца противоположна направлению вектора[v, В]. Если заряженная частица движется параллельно силовым линиям магнитного поля, то угол между векторами скорости и магнитной индукции равен нулю. Следовательно, сила Лоренца на такой заряд не действует (sin0 = 0,F_л= 0). Если же заряд будет двигаться перпендикулярно силовым линиям магнитного поля, то угол между векторами скорости и магнитной индукции равен 90⁰. В этом случае сила Лоренца имеет максимально возможное значение: F_л=qvB. Сила Лоренца всегда перпендикулярна скорости движения заряда. Это означает, что сила Лоренца не может изменить величину скорости движения, но изменяет её направление.