
- •Кинематика криволинейного движения. Векторный способ описания движения частицы. Вектор перемещения, мгновенной скорости, мгновенного ускорения.
- •Координатный способ описания движения. Модули вектора мгновенной скорости и вектора мгновенного ускорения.
- •Ускорение полное, нормальное, тангенциальное. Путь, пройденный частицей. Радиус кривизны траектории.
- •Масса. Сила. Центральные, консервативные, диссипативные силы. Принцип суперпозиции сил. Примеры.
- •Законы Ньютона.
- •Импульс материальной точки. Импульс системы материальных точек. Закон сохранения импульса.
- •Центр масс. Координаты центра масс. Теорема о движении центра масс.
- •Основной закон динамики поступательного движения.
- •Работа постоянной силы. Кинетическая энергия. Связь приращения кинетической энергии с работой силы.
- •Консервативная сила. Потенциальная энергия. Потенциальная энергия и ее связь с консервативной силой. Работа консервативной силы. Закон сохранения механической энергии.
- •Момент импульса для материальной точки. Момент импульса материальной точки массой m, движущейся с постоянной по величине скоростью V по окружности радиуса r.
- •Момент силы и момент импульса частицы относительно полюса. Уравнение моментов относительно полюса. Момент импульса и момент силы относительно оси. Уравнение моментов относительно оси.
- •Момент инерции тела относительно неподвижной оси. Теорема Штейнера.
- •Момент инерции. Момент инерции обруча относительно оси, перпендикулярной плоскости обруча и проходящей через центр масс обруча.
- •Момент инерции. Момент инерции стержня относительно оси, перпендикулярно стержню и проходящий через центр масс стержня.
- •Основной закон динамики вращательного движения.
- •Закон сохранения момента импульса.
- •Кинетическая энергия вращающегося тела. Работа внешних сил при вращении твердого тела вокруг неподвижной оси. Кинетическая энергия твердого тела при плоском вращении.
- •Работа при перемещении заряда в электростатическом поле.
- •Теорема о циркуляции вектора напряженности электрического поля.
- •Поток вектора напряженности электростатического поля через некоторую поверхность. Теорема Гаусса для напряженности электрического поля.
- •Теорема Гаусса для электростатического поля в вакууме. Определение напряженности поля точечного заряда с помощью теоремы Гаусса.
- •Теорема Гаусса для электростатического поля. Расчет напряженности поля равномерно заряженной сферы радиуса r с известной поверхностной плотностью заряда
- •Теорема Гаусса для электростатического поля. Расчет поля бесконечного прямолинейного провода, заряженного с линейной плотностью заряда .
- •Теорема Гаусса для электростатического поля в вакууме. Расчет поля равномерно заряженного по объему шара с известной объемной плотностью заряда
- •Энергия электрического поля и ее локализация в пространстве. Выразить энергию заряженного конденсатора через напряженность конденсатора.
- •Магнитное поле. Магнитная индукция. Силовые линии магнитного поля. Сила Лоренца.
- •Закон Био-Савара-Лапласа для магнитной индукции поля, создаваемого элементом тока. Принцип суперпозиции магнитных полей.
- •Магнитное поле, создаваемое равномерно движущимся зарядом.
- •Сила Лоренца. Движение заряда по окружности в постоянном магнитном поле.
- •Магнитное поле кругового тока. Магнитное поле в центре кругового тока.
- •Магнитное поле прямого бесконечного проводника с током.
- •Сила Ампера. Взаимодействие параллельных проводников с током.
- •Теорема о циркуляции вектора магнитной индукции. Поток магнитной индукции.
- •Явление электромагнитной индукции. Правило Ленца. Закон электромагнитной индукции Фарадея.
- •Электродвижущая сила, возникающая в проводнике, движущемся в магнитном поле.
- •Явление самоиндукции. Электродвижущая сила самоиндукции. Индуктивность контура.
- •Энергия магнитного поля. Индуктивность соленоида. Энергия магнитного поля в соленоиде.
Кинематика криволинейного движения. Векторный способ описания движения частицы. Вектор перемещения, мгновенной скорости, мгновенного ускорения.
 Криволинейные
движения –
движения, траектории которых представляют
собой не прямые, а кривые линии.
Криволинейное движение – это всегда
движение с ускорением, даже если по
модулю скорость постоянна. Криволинейное
движение с постоянным ускорением всегда
происходит в той плоскости, в которой
находятся векторы ускорения и начальные
скорости точки. В случае криволинейного
движения с постоянным ускорением в
плоскости xOy проекции vxи vy ее
скорости на оси Ox и Oy и
координаты x и y точки
в любой момент времени t определяется
по формулам
Криволинейные
движения –
движения, траектории которых представляют
собой не прямые, а кривые линии.
Криволинейное движение – это всегда
движение с ускорением, даже если по
модулю скорость постоянна. Криволинейное
движение с постоянным ускорением всегда
происходит в той плоскости, в которой
находятся векторы ускорения и начальные
скорости точки. В случае криволинейного
движения с постоянным ускорением в
плоскости xOy проекции vxи vy ее
скорости на оси Ox и Oy и
координаты x и y точки
в любой момент времени t определяется
по формулам
 .
Частным случаем
криволинейного движения – является
движение по окружности. Движение по
окружности, даже равномерное, всегда
есть движение ускоренное: модуль скорости
все время направлен по касательной к
траектории, постоянно меняет направление,
поэтому движение по окружности всегда
происходит с центростремительным
ускорением
.
Частным случаем
криволинейного движения – является
движение по окружности. Движение по
окружности, даже равномерное, всегда
есть движение ускоренное: модуль скорости
все время направлен по касательной к
траектории, постоянно меняет направление,
поэтому движение по окружности всегда
происходит с центростремительным
ускорением
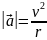 , где r –
радиус окружности. Вектор ускорения
при движении по окружности направлен
к центру окружности и перпендикулярно
вектору скорости. При криволинейном
движении ускорение можно представить
как сумму нормальной
, где r –
радиус окружности. Вектор ускорения
при движении по окружности направлен
к центру окружности и перпендикулярно
вектору скорости. При криволинейном
движении ускорение можно представить
как сумму нормальной  и
тангенциальной
и
тангенциальной  составляющих:
составляющих:
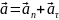 ,
-
нормальное (центростремительное)
ускорение, направлено к центру кривизны
траектории и характеризует изменение
скорости по направлению:
,
-
нормальное (центростремительное)
ускорение, направлено к центру кривизны
траектории и характеризует изменение
скорости по направлению:
 v
– мгновенное
значение скорости, r –
радиус кривизна траектории в данной
точке.
v
– мгновенное
значение скорости, r –
радиус кривизна траектории в данной
точке.
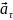 -
тангенциальное (касательное) ускорение,
направлено по касательной к траектории
и характеризует изменение скорости по
модулю.
-
тангенциальное (касательное) ускорение,
направлено по касательной к траектории
и характеризует изменение скорости по
модулю.
Полное ускорение,
с которым движется материальная точка,
равно:
 .
.
Кроме центростремительного
ускорения, важнейшими характеристиками
равномерного движения по окружности
являются период и частота обращения.
Период
обращения—
это время, за которое тело совершается
один оборот.
 где t —
время обращения, п —
число оборотов, совершенных за это
время. Частота
обращения—
это величина, численно равная числу
оборотов, совершенных за единицу времени.
где t —
время обращения, п —
число оборотов, совершенных за это
время. Частота
обращения—
это величина, численно равная числу
оборотов, совершенных за единицу времени.
 Измеряется
частота в 1/с. Период и частота — величины
взаимно обратные. Если тело, двигаясь
по окружности со скоростью v, делает
один оборот, то пройденный этим телом
путь можно найти, умножив скорость v на
время одного оборота: l
= vT. С другой
стороны, этот путь равен длине окружности
2πr.
Поэтому vT=2πr,
T=2πr/v=
ω
/2π,
Измеряется
частота в 1/с. Период и частота — величины
взаимно обратные. Если тело, двигаясь
по окружности со скоростью v, делает
один оборот, то пройденный этим телом
путь можно найти, умножив скорость v на
время одного оборота: l
= vT. С другой
стороны, этот путь равен длине окружности
2πr.
Поэтому vT=2πr,
T=2πr/v=
ω
/2π,
 где ω (с-1) - угловая
скорость. При неизменной частоте
обращения центростремительное ускорение
прямо пропорционально расстоянию от
движущейся частицы до центра вращения.
где ω (с-1) - угловая
скорость. При неизменной частоте
обращения центростремительное ускорение
прямо пропорционально расстоянию от
движущейся частицы до центра вращения.
Угловая скорость (ω)
– величина, равная отношению угла
поворота радиуса, на котором находится
вращающаяся точка, к промежутку времени,
за который произошел этот поворот:
 .
Связь между линейной и угловой скоростями:
v= ωr.
.
Связь между линейной и угловой скоростями:
v= ωr.
Движение тела можно считать известным лишь тогда, когда известно, как движется каждая его точка. Самое простое движение твердых тел – поступательное. Поступательным называется движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается параллельно самой себе.
Векторный способ
описания движения частицы В
этом случае положение частицы задается
её радиус-вектором 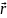 .
Геометрическое место концов радиус-вектора
представляет кривую, называемую траекторией.
Зависимость радиус-вектора частицы от
времени
.
Геометрическое место концов радиус-вектора
представляет кривую, называемую траекторией.
Зависимость радиус-вектора частицы от
времени  называется кинематическим
уравнением движения.
С геометрической
точки зрения -- это
уравнение траектории. Изменение
радиус-вектора
за
время ∆t называется перемещением:
называется кинематическим
уравнением движения.
С геометрической
точки зрения -- это
уравнение траектории. Изменение
радиус-вектора
за
время ∆t называется перемещением:  .
Длина дуги траектории между этими
точками ∆l называется путем.
Важнейшей кинематической характеристикой
движения является скорость.
.
Длина дуги траектории между этими
точками ∆l называется путем.
Важнейшей кинематической характеристикой
движения является скорость.
Скоростью частицы
называется векторная величина,
определяемая равенством ,
иначе говоря, скорость
- это производная от радиус-вектора по
времени. Из
определения следует, что скорость
,
иначе говоря, скорость
- это производная от радиус-вектора по
времени. Из
определения следует, что скорость 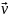 направлена
по касательной к траектории. Величина
скорости
направлена
по касательной к траектории. Величина
скорости
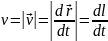 ,
где l -- путь, пройденный вдоль
траектории.
Иногда используется
понятие средней
скорости:
это векторная величина, равная отношению
перемещения ко времени, т.е.
,
где l -- путь, пройденный вдоль
траектории.
Иногда используется
понятие средней
скорости:
это векторная величина, равная отношению
перемещения ко времени, т.е.
 Скорость
изменения скорости частицы по времени,
т.е. вектор
Скорость
изменения скорости частицы по времени,
т.е. вектор
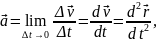 называется ускорением частицы. Таким
образом, зная кинематический закон
движения, можно простым дифференцированием
по времени найти скорость и ускорение
в любой момент времени (так называемая
прямая задача кинематики). Наоборот,
зная ускорение частицы, а также начальные
условия, т.е.
положение
называется ускорением частицы. Таким
образом, зная кинематический закон
движения, можно простым дифференцированием
по времени найти скорость и ускорение
в любой момент времени (так называемая
прямая задача кинематики). Наоборот,
зная ускорение частицы, а также начальные
условия, т.е.
положение  и
скорость
и
скорость 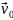 частицы
в начальный момент времени, можно найти
траекторию движения частицы
частицы
в начальный момент времени, можно найти
траекторию движения частицы  (обратная
задача кинематики).
(обратная
задача кинематики).
Вектор перемещения –вектор проведенный из начальной точки в конечную точку траектории
В ектор
мгновенной скорости –
физическая величина равная пределу, к
которому стремиться средняя скорость
при бесконечном уменьшении промежутка
времени Δt:
ектор
мгновенной скорости –
физическая величина равная пределу, к
которому стремиться средняя скорость
при бесконечном уменьшении промежутка
времени Δt:
Вектор мгновенной скорости направлен по касательной к траектории движения тела
Вектор мгновенного
ускорения – придел
приращения скорости ко времени за
которое оно произошло при стремлении
промежутка времени к нулю.

