- •Доказательство.
- •10)Линейная зависимость и независимость векторов. Базис, разложение векторов по базису.
- •14)Смешанное произведение векторов и его свойства. Условие компланарности трех векторов.
- •31)Предел переменной величины. Бесконечно большая переменная величина.
- •32)Предел функции в точке и на бесконечности. Односторонние пределы. Необходимые и достаточные условия существования пределов.
- •39)Непрерывность функции в точке. Точка разрыва и их классификация.
- •40)Асимптоты.
- •Замечание
- •45)Производная логарифмической функции. Логарифмическое дифференцирование .Производная показательно-степенной функции.(см.43)
14)Смешанное произведение векторов и его свойства. Условие компланарности трех векторов.
Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.
Смешанное произведение векторов a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:
a · [b × c] = |
ax |
ay |
az |
bx |
by |
bz |
|
cx |
cy |
cz |
Свойства смешанного произведения векторов
Геометрический смысл смешанного произведения.
Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами: Vпарал = |a · [b × c]|
Геометрический смысл смешанного произведения.
Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:
Vпир = |
1 |
|a · [b × c]| |
6 |
Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
a · [b × c] = b · (a · c) - c · (a · b)
a · [b × c] = b · [c × a] = c · [a × b] = -a · [c × b] = -b · [a × c] = -c · [b × a]
a · [b × c] + b · [c × a] + c · [a × b] = 0 - тождество Якоби.
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
|
|
Условия компланарности векторов
Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю.
Для 3-х векторов. Три вектора компланарны если они линейно зависимы.
Для n векторов. Вектора компланарны если среди них не более двух линейно независимых векторов.
15)Деление отреза в заданном направлении.
Формулы деления отрезка в данном отношении на плоскости
Если
известны две точки плоскости ![]() ,
то координаты точки
,
то координаты точки ![]() ,
которая делит отрезок
,
которая делит отрезок ![]() в
отношении
в
отношении ![]() ,
выражаются формулами:
,
выражаются формулами:
![]()
Формулы деления отрезка в данном отношении в пространстве
Если
известны две точки пространства ![]() ,
то координаты точки
,
то координаты точки ![]() ,
которая делит отрезок
в
отношении
,
выражаются формулами:
,
которая делит отрезок
в
отношении
,
выражаются формулами:
![]() .
.
Формулы координат середины отрезка
![]()
16)Прямая на плоскости. Различные виды уравнений прямой.
Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0,причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой.
Виды:
1.y=kx+b, k=tga
2.y-y0=k(x-x0) , k=tga-уравнение прямой ,проходящей через точку М с заданным угловым коэффициентом к
3.Ax+By+C=0, A^2+B^2 не равно 0- уравнение вектора нормали прямой N=(A,B)
4.A(x-x0)+B(y-y0)=0-уравнение прямой проходящей через точку М с заданным вектором нормали N=(A,B)
5.x-x0/m=y-y0/n, m^2+n^2 не равно 0-каноническое уравнение прямой (направляющий вектор S=(m,n), M(x0,y0))
6.x-x1/x2-x1=y-y1/y2-y1-уравнение прямой ,проходящей через две различные точки M(x1;y1) u M(x2;y2)
Угол между двумя прямыми l1:y=k1x+b1 и l2:k2y=b2 определяется по формуле:
Tga=+-(k2-k1)/1+k1*k2>=0
17)Угол между двумя прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
Угол между двумя прямыми l1:y=k1x+b1 и l2:k2y=b2 определяется по формуле:
Tga=+-(k2-k1)/1+k1*k2>=0
Условия параллельности двух прямых:
а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
k1 = k2.
б) Для случая, когда прямые заданы уравнениями в общем виде A1x + B1y + C1 = 0,
A2x + B2y + C2 = 0,
необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.
![]()
![]()
![]()
![]()
Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
![]()
![]()
![]()
![]()
24)Взаимное расположение прямой и плоскости в пространстве.Точка пересечения прямой и плоскости.
1)Взаимное расположение прямой и плоскости в пространстве.
Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
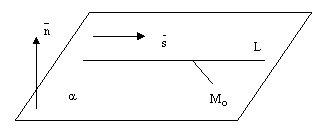
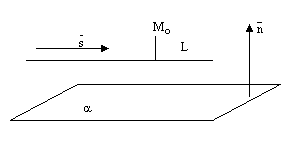
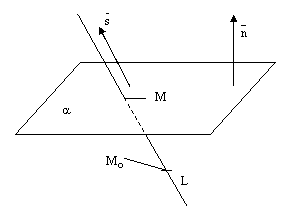
рис.8.
Теорема.
Пусть плоскость ![]() задана
общим уравнением
задана
общим уравнением ![]() ,
,
а
прямая L задана каноническими
уравнениями ![]()
или параметрическими уравнениями
![]() ,
, ![]() ,
,
в
которых ![]() – координаты нормального вектора плоскости
,
– координаты нормального вектора плоскости
, ![]() – координаты произвольной
фиксированной точки прямой L,
– координаты произвольной
фиксированной точки прямой L, ![]() –
–
координаты направляющего вектора прямой L. Тогда:
1)
если ![]() ,
то прямая L пересекает плоскость
в
точке, координаты которой
,
то прямая L пересекает плоскость
в
точке, координаты которой ![]() можно
найти из системы уравнений
можно
найти из системы уравнений
![]() ;
(7)
;
(7)
2)
если ![]() и
и ![]() ,
то прямая лежит на плоскости;
,
то прямая лежит на плоскости;
3)
если
и ![]() ,
то прямая параллельна плоскости.
,
то прямая параллельна плоскости.
Доказательство.
Условие ![]() говорит
о том, что вектроры
говорит
о том, что вектроры ![]() и
и ![]() не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координатыточки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальные уравнения системы,
находим координаты искомой
точки.
не
ортогональны, а значит прямая не
параллельна плоскости и не лежит в
плоскости, а значит пересекает ее в
некоторой точке М. Координатыточки
М удовлетворяют как уравнению плоскости,
так и уравнениям прямой, т.е. системе
(7). Решаем первое уравнение системы (7)
относительно неизвестной t и затем,
подставляя найденное значение t в
остальные уравнения системы,
находим координаты искомой
точки.
Если ![]() ,
то это означает, что
,
то это означает, что ![]() .
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
и координаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка
.
А такое возможно лишь тогда, когда прямая
лежит на плоскости или параллельна ей.
Если прямая лежит на плоскости, то любая
точка прямой является точкой плоскости
и координаты любой
точки прямой удовлетворяют уравнению
плоскости. Поэтому достаточно проверить,
лежит ли на плоскости точка
.
Если
,
то точка ![]() –
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
–
лежит на плоскости, а это означает, что
и сама прямая лежит на плоскости.
Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.
Теорема доказана.
2)Найти
точку пересечения прямой ![]() и
плоскости
и
плоскости ![]() .
.
1. Находим параметрические уравнения прямой. Для этого полагаем
![]() ,
,
откуда получаем
![]()
2. Подставляя
эти выражения для ![]() в
уравнение плоскости и решая его
относительно
в
уравнение плоскости и решая его
относительно ![]() ,
находим значение параметра
,
находим значение параметра ![]() ,
при котором происходит пересечение
прямой и плоскости.
,
при котором происходит пересечение
прямой и плоскости.
3. Найденное
значение ![]() подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:
подставляем
в параметрические уравнения прямой и
получаем искомые координаты точки
пересечения:
![]()
Замечание. Если
в результате решения уравнения
относительно параметра
получим
противоречие, то прямая и плоскость
параллельны (это эквивалентно условию ![]() ).
).
25)Канонические уравнения окружности,эллипса,гиперболы и параболы.
30)Основные элементарные функции и их графики.
1. |
y = k x ,где k - постоянная величина ( коэффициент пропорциональности ). График прямой пропорциональности – прямая
линия, проходящая через начало координат и образующая
с осью X угол
|
2. |
Л A x + B y = C ,где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
|
3. |
О y = k / x ,где k - постоянная величина. График обратной пропорциональности – гипербола ( рис.10 ). В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.
|
5. |
С
Если n – целые, степенные функции имеют смысл и при x < 0, но их графики имеют различный вид в зависимости от того, является ли n чётным числом или нечётным. На рис.15 показаны две такие степенные функции: для n= 2 и n = 3.
При n = 2 функция чётная и её график симметричен относительно оси Y. При n = 3 функция нечётная и её график симметричен относительно начала координат. Функция y = x 3 называется кубической параболой. На
рис.16 представлена функция |
6. |
П
|
7. |
Л
|
8. |
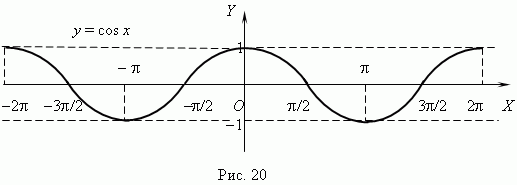
Т График
функции y = cos x представлен
на рис.20; это также синусоида, полученная
в результате перемещения
графика y = sin x вдоль
оси Х влево
на
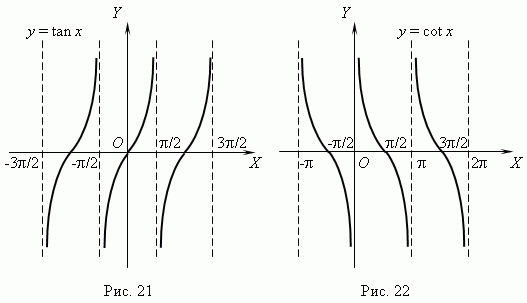
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Из графиков видно, что эти функции: периодические (их период ), неограниченные, в целом не монотонные, но имеют интервалы монотонности (какие?), разрывные (какие точки разрыва имеют эти функции?). Область определения и область значений этих функций:
|
9. |
Обратные тригонометрические функции. |
Ф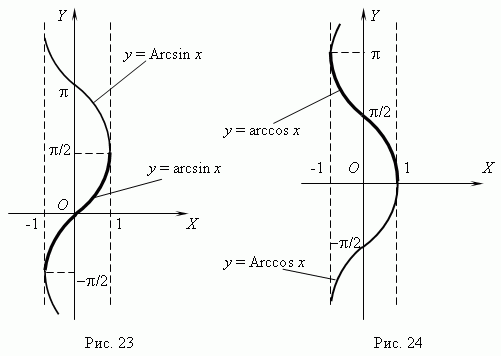 ункции y = Arcsin x (
рис.23 ) и y = Arccos x (
рис.24 ) многозначные, неограниченные; их
область определения
и область значений
соответственно: 1
ункции y = Arcsin x (
рис.23 ) и y = Arccos x (
рис.24 ) многозначные, неограниченные; их
область определения
и область значений
соответственно: 1 ![]() x
+1 и
x
+1 и ![]() < y +
.
Поскольку эти функции
многозначные,не рассматриваемые в
элементарной математике, в качестве
обратных тригонометрических функций
рассматриваются их главные
значения: y = arcsin x и y = arccos x;
их графики выделены на рис.23 и рис.24 жирными
линиями.
< y +
.
Поскольку эти функции
многозначные,не рассматриваемые в
элементарной математике, в качестве
обратных тригонометрических функций
рассматриваются их главные
значения: y = arcsin x и y = arccos x;
их графики выделены на рис.23 и рис.24 жирными
линиями.
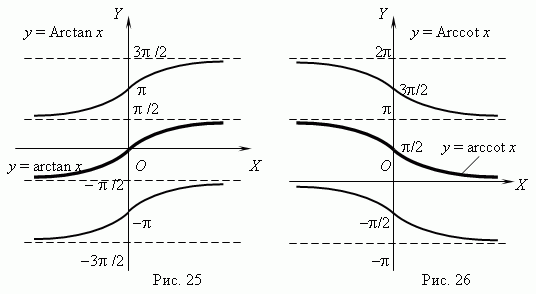
Функции y = Arctan x ( рис.25 ) и y = Arccot x ( рис.26 ) - многозначные, неограниченные; их область определения: x + . Их главные значения y = arctan x и y = arccot x рассматриваются в качестве обратных тригонометрических функций; их графики выделены на рис.25 и рис.26 жирными ветвями.

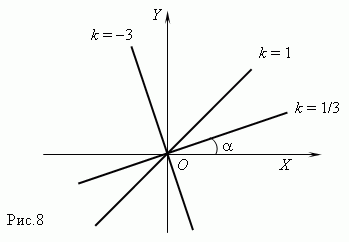 Пропорциональные
величины. Если переменные y и x прямо пропорциональны, то
функциональная зависимость между
ними выражается уравнением:
Пропорциональные
величины. Если переменные y и x прямо пропорциональны, то
функциональная зависимость между
ними выражается уравнением: 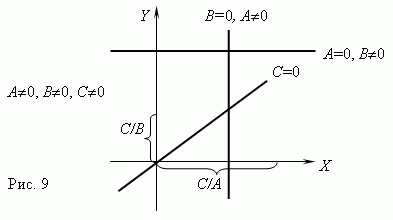 инейная
функция. Если переменные y и x связаны
уравнением 1-ой
степени:
инейная
функция. Если переменные y и x связаны
уравнением 1-ой
степени: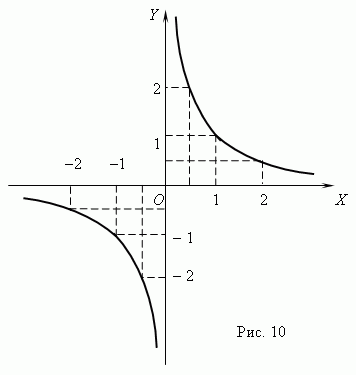 братная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная
зависимость между
ними выражается уравнением:
братная пропорциональность. Если переменные y и x обратно пропорциональны, то функциональная
зависимость между
ними выражается уравнением: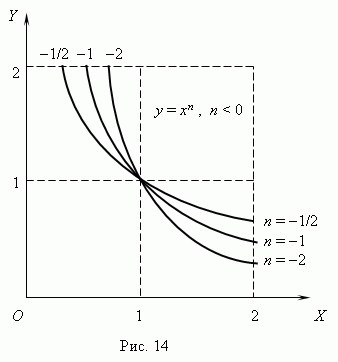 тепенная
функция. Это функция: y = axn,
где a,
n –
постоянные. При n =
1 получаем прямую
пропорциональность: y = ax;
при n =
2 - квадратную
параболу ;
при n = 1
- обратную
пропорциональность или гиперболу.
тепенная
функция. Это функция: y = axn,
где a,
n –
постоянные. При n =
1 получаем прямую
пропорциональность: y = ax;
при n =
2 - квадратную
параболу ;
при n = 1
- обратную
пропорциональность или гиперболу.

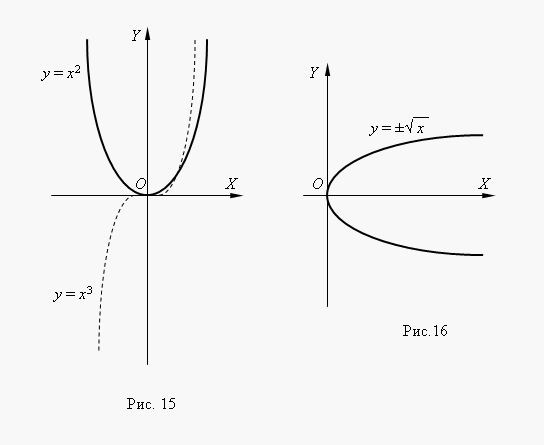
 оказательная
функция. Функция y = ax, где a - положительное
постоянное число, называется показательной
функцией. Аргумент x принимает любые действительные
значения;
в качестве значений функции
рассматриваются только
положительные числа,
так как иначе мы имеем многозначную
функцию. Так, функция y =
81x имеет
при x = 1/4 четыре
различных
значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста !).Но
мы рассматриваем в качестве значения
функции только y =
3.
оказательная
функция. Функция y = ax, где a - положительное
постоянное число, называется показательной
функцией. Аргумент x принимает любые действительные
значения;
в качестве значений функции
рассматриваются только
положительные числа,
так как иначе мы имеем многозначную
функцию. Так, функция y =
81x имеет
при x = 1/4 четыре
различных
значения: y = 3, y = 3, y = 3 i и y = 3 i (проверьте, пожалуйста !).Но
мы рассматриваем в качестве значения
функции только y =
3.
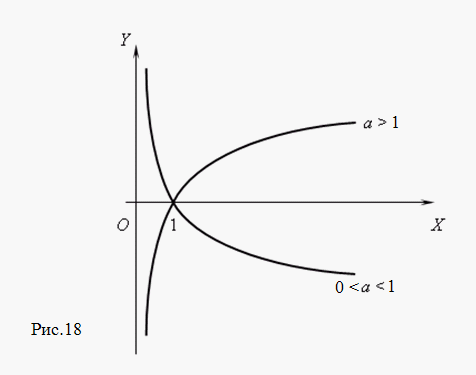 огарифмическая
функция. Функция y = log a x,
где a –
постоянное положительное
число, не
равное 1, называется логарифмической.
Эта функция является обратной к
показательной функции;
огарифмическая
функция. Функция y = log a x,
где a –
постоянное положительное
число, не
равное 1, называется логарифмической.
Эта функция является обратной к
показательной функции;
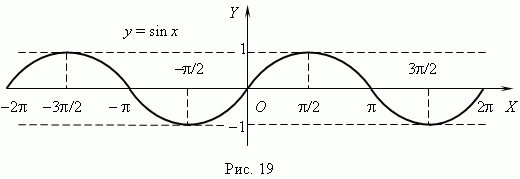 ригонометрические
функции. При построении тригонометрических
функций мы используем радианную меру измерения
углов. Тогда функция y = sin x представляется
графиком ( рис.19 ).
Эта кривая называется синусоидой.
ригонометрические
функции. При построении тригонометрических
функций мы используем радианную меру измерения
углов. Тогда функция y = sin x представляется
графиком ( рис.19 ).
Эта кривая называется синусоидой.