1)Определители и их свойства:

Каждой матрице н-го порядка можно поставить в соответствие число, которое называется определителем или детерминантом.

Определитель не меняется при транспонировании.

1. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

2. Если в определителе переставить две строки, определитель поменяет знак.

3. Определитель, содержащий две одинаковые строки, равен нулю.

4. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

5. Определитель, содержащий две пропорциональные строки, равен нулю.

6. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a_{i j} = b_j + c_j (j=n), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

7. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.

2)Решение систем методом Крамера:

Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:

Составить определитель матрицы системы , и убедиться, что он не равен нулю, т.е. Δ≠0.

Для каждой переменной xi(i=1,n¯¯¯¯¯¯¯) необходимо составить определитель Δxi, полученный из определителя Δ заменой i-го столбца столбцом свободных членов заданной СЛАУ.

3)Матрица. Действия над матрицами.

Матрицей A=A_mn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.

Элементы матрицы a_ij, у которых i=j, называются диагональными и образуют главную диагональ.

Для квадратной матрицы (m=n) главную диагональ образуют элементы a₁₁, a₂₂,..., a_nn .

Равенство матриц.

A=B, если порядки матриц A и B одинаковы и a_ij=b_ij (i=1,2,...,m; j=1,2,...,n)

Действия над матрицами.

1. Сложение матриц - поэлементная операция

2. Вычитание матриц - поэлементная операция

3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы

5. Возведение в степень

m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A' Строки и столбцы поменялись местами

Свойства операций над матрицами

A+B=B+A

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(A')'=A

(λA)'=λ(A)'

(A+B)'=A'+B'

(AB)'=B'A'

Виды матриц

Прямоугольные: m и n - произвольные положительные целые числа

Квадратные: m=n

Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

Матрица столбец: n=1.

Диагональная матрица: m=n и a_ij=0, если i≠j.

Единичная матрица: m=n

Нулевая матрица: a_ij=0, i=1,2,...,m j=1,2,...,n

Треугольная матрица: все элементы ниже главной диагонали равны 0.

4)Обратная матрица:

Невырожденной называется квадратная матрица, определитель которой не равен нулю. Квадратная матрица называется вырожденной, если ее определитель равен нулю.

Квадратная матрица   называется обратной к невырожденной матрице   , если  , где   - это единичная матрица соответствующего порядка Замечание

Обратная матрица существует только для квадратных матриц с не равными нулю определителями.

Свойства обратной матрицы:

1°    

2°    

3°    

4°    

5)Ранг матрицы и его свойства:

Рангом матрицы называется наивысший порядок отличных от нуля миноров.

Свойства:

Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.

Ранг прямоугольной матрицы не превышает меньшего из двух чисел   и   т.е.  .

Для квадратной матрицы  -го порядка   только тогда, когда матрица невырожденная.

В случае квадратной матрицы если   то определитель матрицы равен нулю.

|Вопрос 7| Теорема Кронекера Капелли

 Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

           Очевидно, что система (1) может быть записана в виде: x1   + x2  + … + xn 

Доказательство.

            1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А->А* не изменяют ранга.

            2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

Пример. Определить совместность системы линейных уравнений:

A =  ~  RgA=2.

A* =             RgA* = 3.

Система несовместна.

 Пример. Определить совместность системы линейных уравнений.

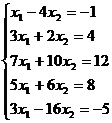                     А =  ;    = 2 + 12 = 14 не равно 0;    RgA = 2;

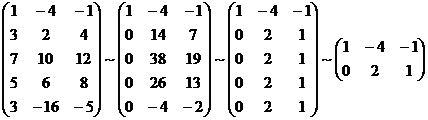
A* =  RgA*=2. Система совместна. Решения: x₁ = 1;  x₂ =1/2.

|Вопрос 8 |Система линейных однородных уравнений

Что такое однородная система линейных уравнений?

Ответ напрашивается сам собой. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:

Совершенно ясно, что однородная система всегда совместна, то есть всегда имеет решение. И, прежде всего, в глаза бросается так называемое тривиальное решение  . Не академично, конечно, но зато доходчиво =) …Чего ходить вокруг да около, давайте выясним, нет ли у данной системы каких-нибудь других решений:

Пример 1

Решить однородную систему линейных уравнений

Решение: чтобы решить  однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

В результате элементарных преобразований получена эквивалентная однородная система  , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

Ответ: 

Сформулируем очевидный критерий: однородная система линейных уравнений имеет только тривиальное решение, если ранг матрицы системы (в данном случае 3) равен количеству переменных (в данном случае   – 3 шт.).

|Вопрос 9| Векторы.Линейные операции над векторами.Проекция вектора на ось.

ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНОЙ АЛГЕБРЫ

Скалярные и векторные величины

Из курса элементарной физики известно, что некоторые физические величины, такие как температура, объем, масса тела, плотность и т.д., определяются только числовым значением. Такие величины называются скалярными величинами, или скалярами.

Для определения же некоторых других величин, таких как сила, скорость, ускорение и тому подобных, кроме числовых значений необходимо задать еще и их направление в пространстве. Величины, которые кроме абсолютной величины характеризуются еще и направлением, называются векторными.

Определение: Вектором называется направленный отрезок, который определяется двумя точками: первая точка определяет начало вектора, а вторая - его конец. Поэтому еще говорят, что вектор - это упорядоченная пара точек.

На рисунке вектор изображается отрезком прямой, на котором стрелкой отмеченное направление от начала вектора к его концу. Например, рис. 2.1.

Если начало вектора совпадает с точкой А, а конец с точкой В, то вектор обозначается АВ. Кроме этого, часто векторы обозначают одной маленькой буквой со стрелкой над ней а. К векторам относится нулевой вектор, у которого начало и конец совпадают. Он обозначается О.

Расстояние между началом и концом вектора называется его длиной, или модулем.

Векторы, параллельные до одной прямой, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной и той же плоскости, называются компланарными.

Нулевой вектор считается коллинеарным к любому вектору. Длина его равна 0.

Определение: Два вектора называются равными, если они: 1)коллинеарны; 2) сонаправлены 3) равны по длине.

Из определения равенства векторов вытекает, что при параллельном переносе вектора получается вектор, равный начальному, потому начало вектора можно разместить в любую точку пространства. Такие векторы (в теоретической механике, геометрии), начало которых можно размещать в любой точке пространства, называют свободными. И именно такие векторы мы будем рассматривать.

Определение: Система векторов называется линейно зависимой, если существуют такие постоянные, среди которых есть хотя бы одна отличная от нуля, и для которых выполняется равенство .

Определение: Базисом в пространстве называются произвольные три некомпланарных вектора, которые взяты в определенной последовательности.

Определение: Если  - базис и вектор , то числа называются координатами вектора в данном базисе.

Координаты вектора будем писать в фигурных скобках после обозначения вектора. Так, например,  означает, что вектор в некотором выбранном базисе имеет разложение: .

Из свойств умножения вектора на число и сложения векторов вытекает утверждение относительно линейных действий над векторами, которые заданы координатами.

Для того, чтобы найти координаты вектора, если известны координаты его начала и конца, необходимо из соответствующей координаты его конца отнять координату начала. 

Линейные операции над векторами

Линейными операциями над векторами называются операции сложения (вычитания) векторов и умножения вектора на число. Рассмотрим их.

Определение: Произведением вектора на число m называется вектор, совпадающий по направлению с вектором, если m>0, имеющий противоположное направление, если отрицательное. Длина этого вектора равна произведению длины вектора на модуль числа.

Пример: Построить вектор b=ma, если m=2 и m=-0.5.

При умножении вектора на число его координаты умножаются на это число.

Определение: Суммой двух векторов называется вектор, который выходит из их общего начала и является диагональю параллелограмма, стороны которого векторы

Итак, для того чтобы построить вектор суммы, надо к концу первого вектора пристроить начало второго, к концу второго пристроить начало третьего и так далее. Тогда вектором суммы и будет вектор, который соединяет начало первого из векторов с концом последнего.

При сложении векторов складываются и их соответствующие координаты

Действительно, если и  ,

то 

Если векторы  и не компланарны, то их сумма является диагональю параллелепипеда, построенного на этих векторах (рис. 2.6)

,

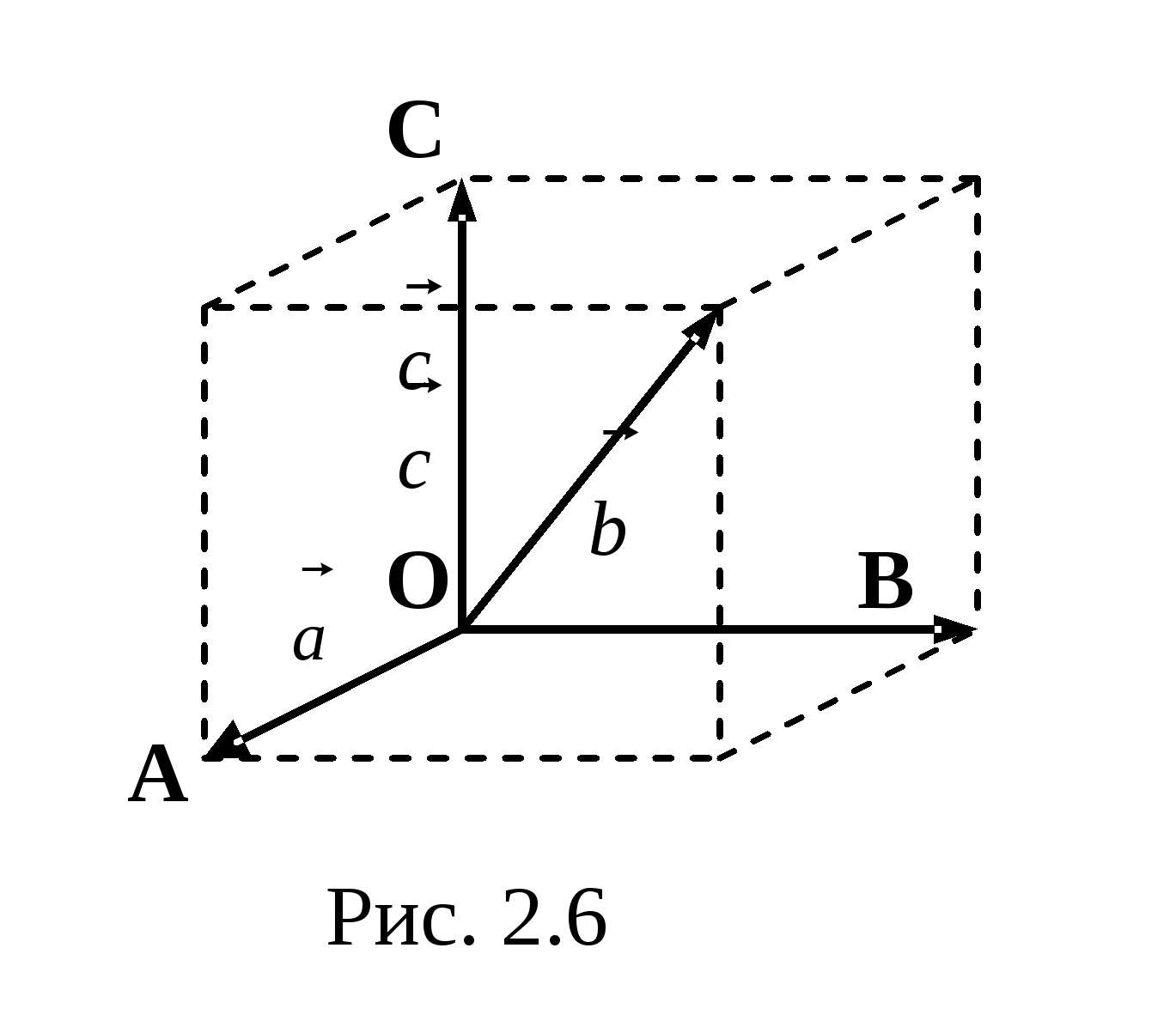
г де

Свойства:

- коммутативность;

- ассоциативность;

- дистрибутивность по отношению к умножению на число

.

Т.е. векторную сумму можно преобразовывать по тем же правилам, что и алгебраическую.

Определение: Разностью двух векторов и называют такой вектор , который при сложении с вектором дает вектор . Т.е.  если . Геометрически представляет собой вторую диагональ параллелограмма, построенного на векторах и с общим началом и направленную из конца вектора в конец вектора (рис. 2.7).

Проекция вектора на ось. Свойства проекций

Вспомним понятие числовой оси. Числовой осью называют прямую, на которой определено:

направление ( → );

начало отсчета (точка О);

отрезок, который принимают за единицу масштаба.

Пусть имеется вектор  и ось . Из точек А и В опустим перпендикуляры на ось . Получим точки а и b - проекции точек и (рис. 2.8 а).

Определение: Проекцией вектора на ось называется длина отрезка ab этой оси, который расположен между основаниями проекций начала и конца вектора на ось . Она берется со знаком плюс, если направление отрезка совпадает с направлением оси проекций, и со знаком минус, если эти направления противоположны. Обозначение: .

Определение: Углом между вектором и осью называется угол  , на который необходимо кратчайшим образом повернуть ось , чтобы она совпадала с направлением вектора .

Найдем  :

На рис.2.8 а представлена:  .

На рис. 2.8 б):  .

Проекция вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью проекций:  .

Свойства проекций:

равные векторы имеют равные проекции;

при умножении вектора на число  его проекция на ось также умножается на то же число;

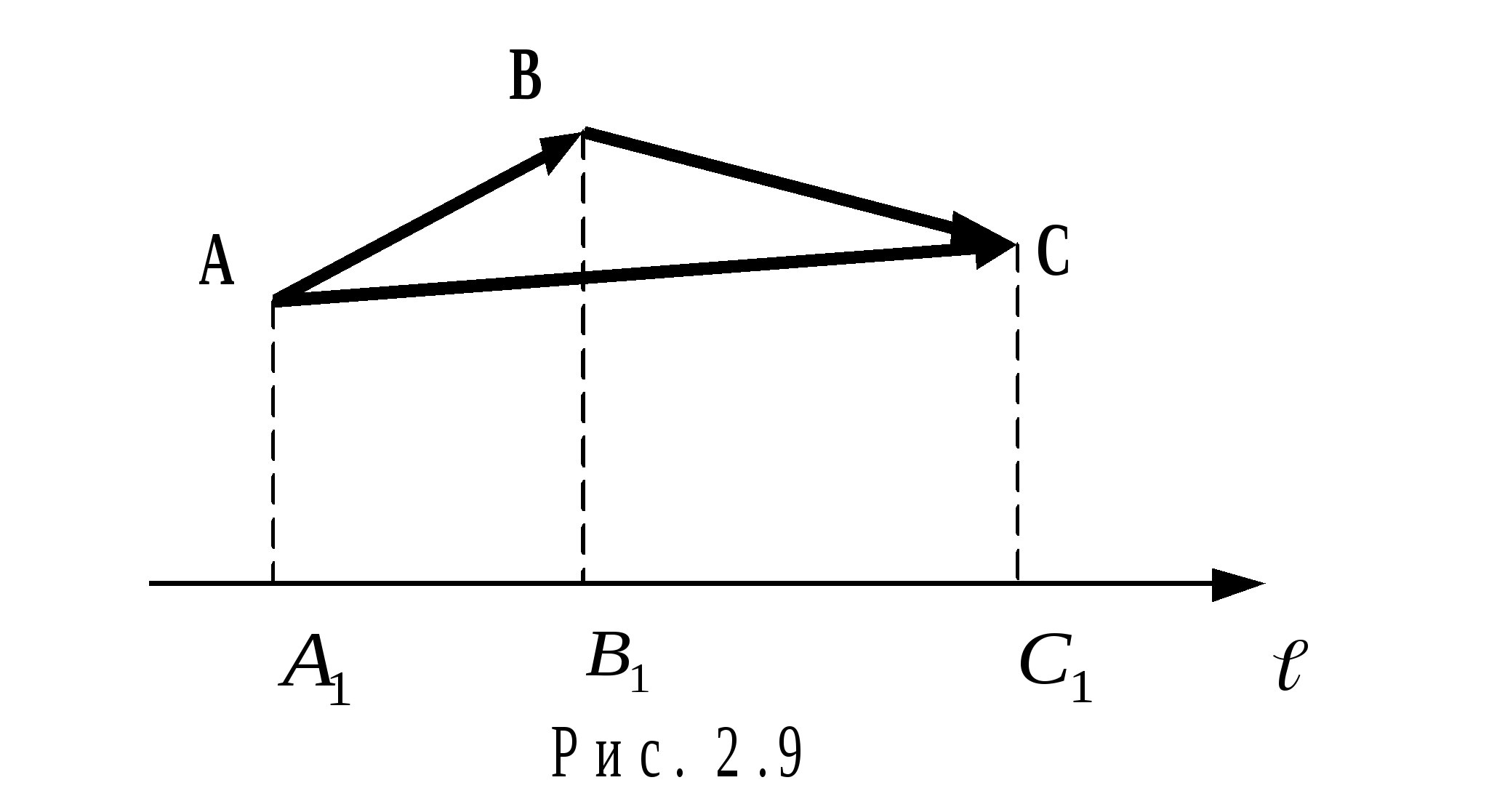
проекция суммы двух векторов на ось равна сумме проекций этих векторов, см. рис. 2.9.

Е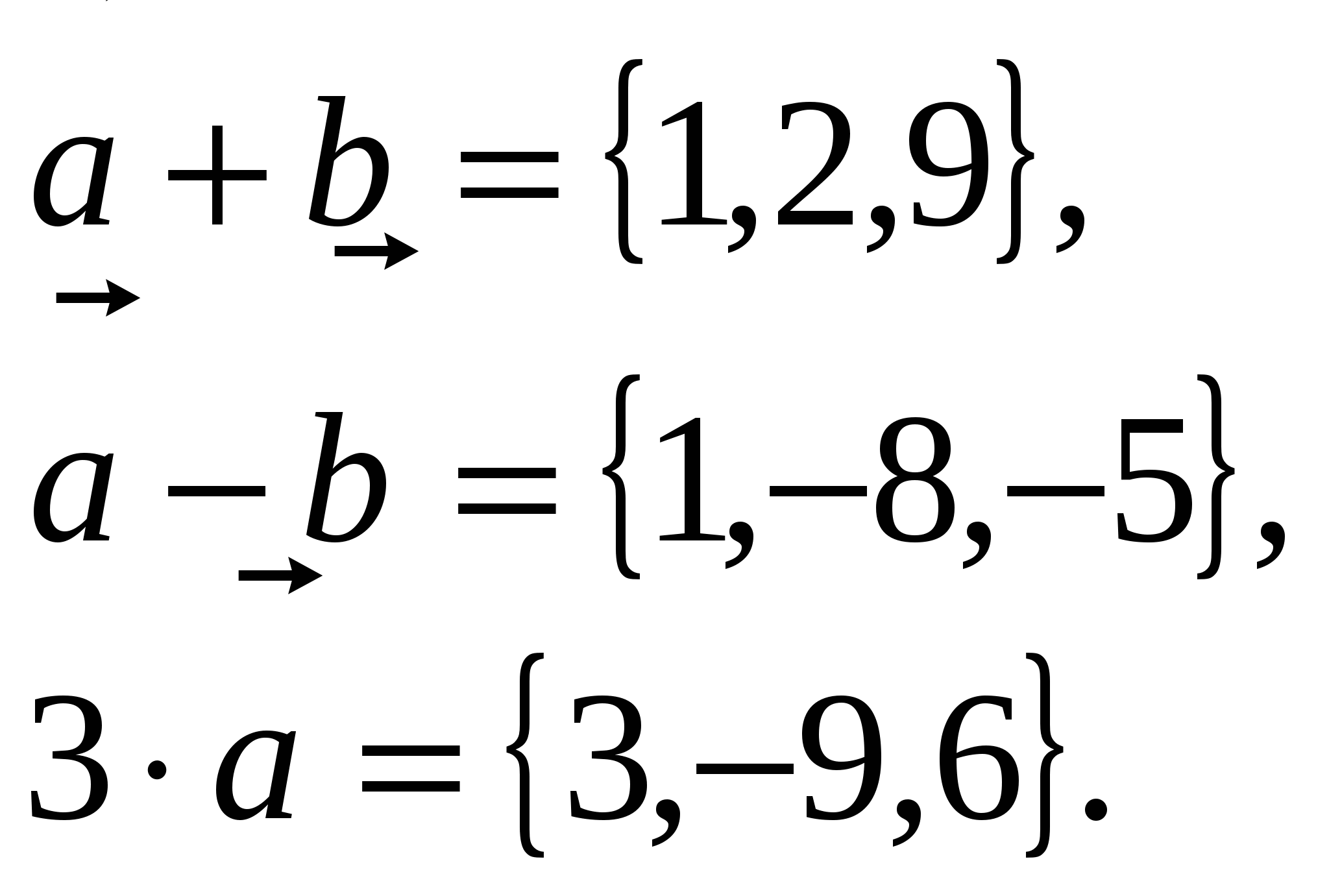 сли  , то векторы называются ортогональными

Пример. Заданы векторы  , . Тогда .

Пример: Если начало вектора находится в точке , а конец в точке , то вектор имеет координаты: .

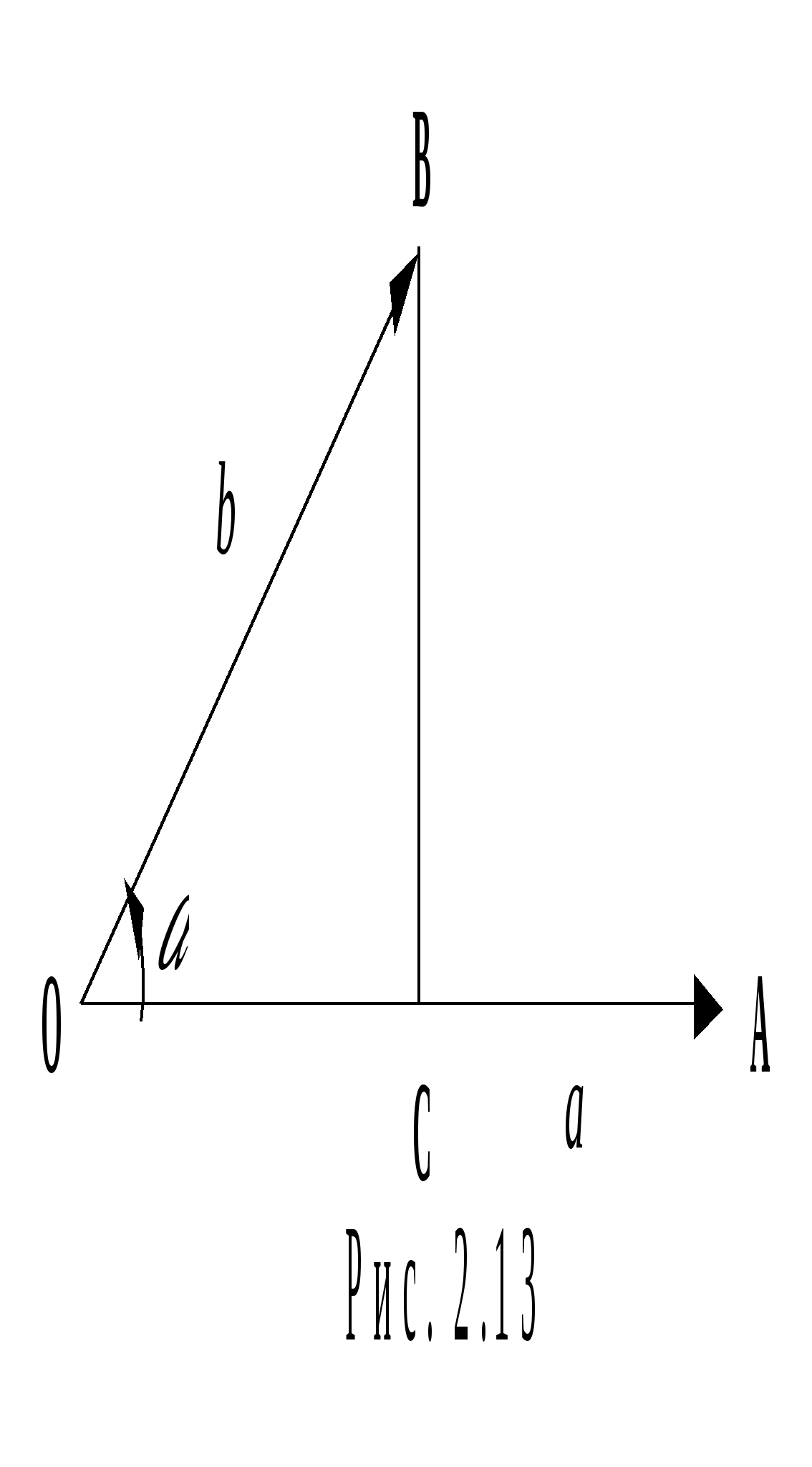Определение: Углом между двумя векторами и называется наименьший угол  (рис. 2.13) между этими векторами, сведенными в общее начало .

Угол между векторами и символически записывают таким образом:  .

Из определения следует, что угол между векторами может изменяться в пределах  .

Если  , то векторы называются ортогональными.

.

Определение: Косинусы углов вектора с осями координат называются направляющими косинусами вектора. Если вектор образует с осями координат углы

,

откуда

.