5. Метод чисел Фибоначчи1

Этот метод применяется, когда число экспериментов заранее задано. Метод чисел Фибоначчи, также как и метод золотого сечения относится к симметричным методам, т.е. точки, в которых выполняются два эксперимента, на основе которых происходит уменьшение отрезка неопределённости, расположены симметрично относительно середины отрезка. Вот только выбор точки происходит на основе других соотношений. Для этого используются числа Фибоначчи: , где и .

Точка определяется из соотношения:

т.е. . Точка делит на две неравные части. Отношение малого отрезка к большему равно . Точка определяется как точка, симметричная к относительно середины отрезка . Поэтому . При этом будет выполняться условие .

В результате экспериментов в точках и у нас получится отрезок неопределённости , содержащий точку , или отрезок неопределённости , содержащий точку . Остающаяся точка делит новый отрезок неопределённости на две неравные части в отношении:

. То есть в методе Фибоначчи остающаяся точка делит отрезок на две неравные части в пропорциях определяемых числами Фибоначчи. Так на -ом шаге это отношение равно а длины отрезков равны: и . Всё это показано на рисунке ХХ.

Рис.4 Результаты первой итерации для метода чисел Фибоначчи

Для того чтобы в свою очередь уменьшить получившийся отрезок неопределённости, надо определить симметричную точку относительно середины отрезка и произвести эксперимент в ней. Этот процесс продолжается, пока не будет проведено экспериментов.

Схема алгоритма

Шаг 1. Задаются Вычисляются числа Фибоначчи . Определяется:

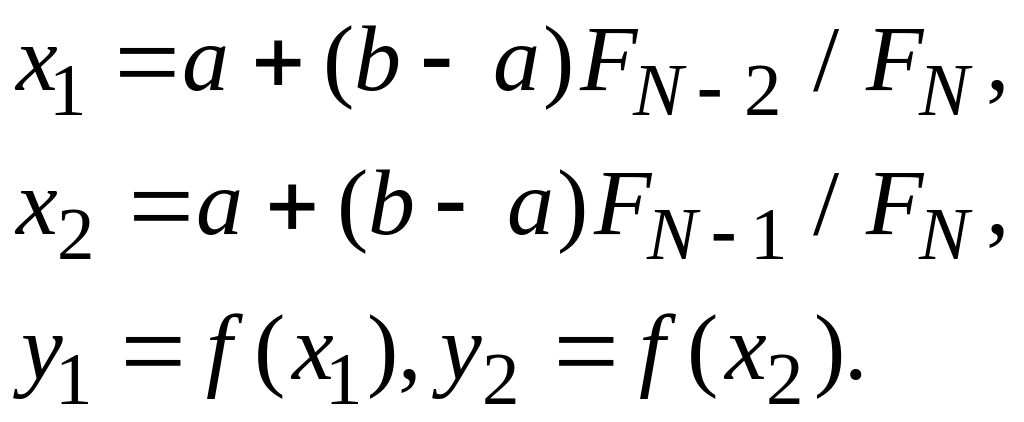
Шаг 2.

а) Если , то полагают и вычисляют .

б) Если , то полагают и вычисляют .

Повторить шаг 2 раза.

Шаг 3. Если , то полагают и . Если , то полагают и .

Закончить поиск.

Длина отрезка неопределённости в методе Фибоначчи .

3 Методы поиска, основанные на аппроксимации целевой функции ( методы 1-го порядка)

Суть этих методов заключается в том, что по полученной в ходе вычислений информации строится аппроксимирующая функция и её минимум принимается за точку очередного вычисления. Такие методы дают хорошие результаты при минимизации достаточно гладких унимодальных функций.

3.1 Метод касательных

Пусть функция выпукла и дифференцируема на . Идея метода состоит в следующем. Пусть - отрезок неопределённости и - результаты вычислений в точках и . По этой информации строится аппроксимирующая функция, представляющую из себя кусочно-линейную функцию, состоящую из касательной к в точке и касательной к в точке .

Рис.5 Иллюстрация для метода касательных

Полученная аппроксимирующая функция есть ломанная состоящая из прямой на и на , где с – точка пересечения касательных. Легко заметить, что при и минимум аппроксимирующей функции достигается в точке . Значение точки пересечения можно определить по формуле

.

В точке производятся вычисления и . Если , то решением задачи будет . Если же , то в качестве следующего отрезка неопределённости будет . Если же , то – отрезок . Процесс повторяется до тех пор, пока или отрезок неопределённости не достигнет заданной точности.

Схема алгоритма

Шаг 1. Заданы . Вычислить .

Шаг 2. Если , то полагаем . Поиск окончен.

Если , то вычислить . Если , то полагаем и поиск окончен. Если , то . Если , то . Повторить шаг 2.