3 Содержание работ по семестрам
Номер варианта для студентов заочной формы обучения определяется по последней цифре номера зачетной книжки. Последняя цифра номера зачетной книжки равна последней цифре номера варианта.
№ варианта |
Контрольные работы |
|
I семестр |
II семестр |
|
1 |
1.1.1, 1.2.1, 1.3.1, 1.4.1, 1.5.1, 1.6.1, 1.7.1, 1.8.1, 1.9.1, 1.10.1 |
2.1.1, 2.2.1, 2.3.1, 2.4.1, 2.5.1, 2.6.1, 2.7.1, 2.8.1, 2.9.1, 2.10.1 |
2 |
1.1.2, 1.2.2, 1.3.2, 1.4.2, 1.5.2, 1.6.2, 1.7.2, 1.8.2, 1.9.2, 1.10.2 |
2.1.2, 2.2.2, 2.3.2, 2.4.2, 2.5.2, 2.6.2, 2.7.2, 2.8.2, 2.9.2, 2.10.2 |
3 |
1.1.3, 1.2.3, 1.3.3, 1.4.3, 1.5.3, 1.6.3, 1.7.3, 1.8.3, 1.9.3, 1.10.3 |
2.1.3, 2.2.3, 2.3.3, 2.4.3, 2.5.3, 2.6.3, 2.7.3, 2.8.3, 2.9.3, 2.10.3 |
4 |
1.1.4, 1.2.4, 1.3.4, 1.4.4, 1.5.4, 1.6.4, 1.7.4, 1.8.4, 1.9.4, 1.10.4 |
2.1.4, 2.2.4, 2.3.4, 2.4.4, 2.5.4, 2.6.4, 2.7.4, 2.8.4, 2.9.4, 2.10.4 |
5 |
1.1.5, 1.2.5, 1.3.5, 1.4.5, 1.5.5, 1.6.5, 1.7.5, 1.8.5, 1.9.5, 1.10.5 |
2.1.5, 2.2.5, 2.3.5, 2.4.5, 2.5.5, 2.6.5, 2.7.5, 2.8.5, 2.9.5, 2.10.5 |
6 |
1.1.6, 1.2.6, 1.3.6, 1.4.6, 1.5.6, 1.6.6, 1.7.6, 1.8.6, 1.9.6, 1.10.6 |
2.1.6, 2.2.6, 2.3.6, 2.4.6, 2.5.6, 2.6.6, 2.7.6, 2.8.6, 2.9.6, 2.10.6 |
7 |
1.1.7, 1.2.7, 1.3.7, 1.4.7, 1.5.7, 1.6.7, 1.7.7, 1.8.7, 1.9.7, 1.10.7 |
2.1.7, 2.2.7, 2.3.7, 2.4.7, 2.5.7, 2.6.7, 2.7.7, 2.8.7, 2.9.7, 2.10.7 |
8 |
1.1.8, 1.2.8, 1.3.8, 1.4.8, 1.5.8, 1.6.8, 1.7.8, 1.8.8, 1.9.8, 1.10.8 |
2.1.8, 2.2.8, 2.3.8, 2.4.8, 2.5.8, 2.6.8, 2.7.8, 2.8.8, 2.9.8, 2.10.8 |
9 |
1.1.9, 1.2.9, 1.3.9, 1.4.9, 1.5.9, 1.6.9, 1.7.9, 1.8.9, 1.9.9, 1.10.9 |
2.1.9, 2.2.9, 2.3.9, 2.4.9, 2.5.9, 2.6.9, 2.7.9, 2.8.9, 2.9.9, 2.10.9 |
10 |
1.1.10, 1.2.10, 1.3.10, 1.4.10, 1.5.10, 1.6.10, 1.7.10, 1.8.10, 1.9.10, 1.10.10 |
2.1.10, 2.2.10, 2.3.10, 2.4.10, 2.5.10, 2.6.10, 2.7.10, 2.8.10, 2.9.10, 2.10.10 |
4 Контрольные задания для I семестра
Задание 1.1.
Даны матрицы А, В, С. Вычислить:
1)
;
2)
;
3)
.
1.1.1 
,
,
.
1.1.2 
,
,
.
1.1.3 
,
,
.
1.1.4 
,
,
.
1.1.5 
,
,
.
1.1.6 
,
,
.
1.1.7 
,
,
.
1.1.8 
,
,
.
1.1.9 
,
,
.
1.1.10 
,
,
.
Задание 1.2.
Найти все решения системы линейных уравнений:
а) по формулам Крамера;
б) методом Гаусса.
1.2.1 |
а)
|
б)
|
1.2.2 |
а)
|
б)
|
1.2.3 |
а)
|
б)
|
1.2.4 |
а)
|
б)
|
1.2.5 |
а)
|
б)
|
1.2.6 |
а)
|
б)
|
1.2.7 |
а)
|
б)
|
1.2.8 |
а)
|
б)
|
1.2.9 |
а)
|
б)
|
1.2.10 |
а)
|
б)
|
Задание 1.3
Даны вершины треугольника АВС. Найти:
а) длины сторон треугольника;
б) тангенс угла между высотой ВН и медианой ВМ треугольника, проведенных из одной вершины;
в) длину высоты ВН;
г) площадь треугольника.
1.3.1 А(4;2), В(2;-5), С(-5;-1).
1.3.2 А(-3;-4), В(2;6), С(7;-2).
1.3.3 А(-2;-7), В(-4;-1), С(4;2).
1.3.4 А(-3;3), В(5;5), С(0;-3).
1.3.5 А(-2;-3), В(0;5), С(7;3).
1.3.6 А(-4;3), В(6;4), С(2;-8).
1.3.7 А(4;-1), В(-4;5), С(5;8).
1.3.8 А(1;6), В(2;-3), С(-5;-2).
1.3.9 А(2;6), В(-1;-4), С(-5;-1).
1.3.10 А(7;0), В(-2;-4), С(-5;5).
Задание 1.4
Пирамида ABCD задана координатами вершин.
а)
Найти угол между векторами
и
.
б) Найти площадь основания ABC.
г) Найти объём пирамиды.
д) Составить уравнение плоскости ABC.
е) Составить канонические уравнения прямой, проходящей через высоту DH.
ж) Найти длину высоты DH.
1.4.1. 
1.4.2 
1.4.3 
1.4.4 
1.4.5 
1.4.6 
1.4.7 
1.4.8 
1.4.9 
1.4.10 
Задание 1.5
Дано уравнение кривой второго порядка.
а) Определить вид кривой. Выписать каноническое уравнение кривой.
б) Привести уравнение кривой к каноническому виду.
в) Определить параметры кривой. В случае эллипса: координаты центра симметрии, полуоси, координаты фокусов. В случае гиперболы: координаты центра симметрии, мнимую и действительную полуоси, уравнения асимптот. В случае параболы: координаты вершины, координаты фокуса, уравнение директрисы.
г) Построить кривую в координатной плоскости.
1.5.1 
.
1.5.2 
.
1.5.3 
.
1.5.4 
.
1.5.5 
.
1.5.6 
.
1.5.7 
1.5.8 
.
1.5.9 
.
1.5.10 
.
Задание 1.6
Вычислить пределы.
1.6.1 |
а)
|
б)
|
|
в)
|
г)
|
1.6.2 |
а)
|
б)
|
|
в)
|
г)
|
1.6.3 |
а)
|
б)
|
|
в)
|
г)
|
1.6.4 |
а)
|
б)
|
|
в)
|
г)
|
1.6.5 |
а)
|
б)
|
|
в)
|
г)
|
1.6.6 |
а)
|
б)
|
|
в)
|
г)
|
1.6.7 |
а)
|
б)
|
|
в)
|
г)
|
1.6.8 |
а)
|
б)
|
|
в)
|
г)
|
1.6.9 |
а)
|
б)
|
|
в)
|
г)
|
1.6.10 |
а)
|
б)
|
|
в)
|
г)
|
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
;
;
;
.
Задание 1.7
Исследовать функции на непрерывность. Найти точки разрыва, определить вид разрыва. Построить график функции по результатам исследования.
1.7.1 |
а)
|
б)
|
||
1.7.2 |
а)
|
б)
|
||
1.7.3 |
а)
|
б)
|
||
1.7.4 |
а)
|
б)
|
||
1.7.5 |
а)
|
б)
|
||
1.7.6 |
а)
|
б)
|
||
1.7.7 |
а)
|
б)
|
||
1.7.8 |
а)
|
б) . |
||
1.7.9 |
а)
|
б)
|
||
1.7.10 |
а)
|
б)
|
||
;
.
;
.
;
.
;
.
;
.
;
.
;
.
;
;
.
;
.
Задание 1.8
Вычислить производные данных функций.
1.8.1 |
а)
|
б)
|
в)
|
1.8.2 |
а)
|
б)
|
в)
|
1.8.3 |
а)
|
б)
|
в)
|
1.8.4 |
а)
|
б)
|
в) . |
1.8.5 |
а)
|
б)
|
в)
|
1.8.6 |
а)
|
б)
|
в)
|
1.8.7 |
а)
|
б)
|
в)
|
1.8.8 |
а)
|
б)
|
в) . |
1.8.9 |
а)
|
б)
|
в)
|
1.8.10 |
а)
|
б)
|
в)
|
;
;
.
;
;
.
;
;
.
;
;
;
;
.
;
;
.
;
;
.
;
;
;
;
.
;
;
.
Задание 1.9
Дана
функция z=f(x;y).
Найти частные производные второго
порядка
,
.
Убедиться, что смешанные производные
и
равны.
1.9.1 |
|
1.9.2 |
|
1.9.3 |
|
1.9.4 |
|
1.9.5 |
|
1.9.6 |
|
1.9.7 |
|
1.9.8 |
|
1.9.9 |
|
1.9.10 |
|
.
.
.
.
.
.
.
.
.
Задание 1.10
Исследовать на экстремум функцию z=f(x;y) в области ее определения:
1.10.1 
.
1.10.2 
.
1.10.3 
.
1.10.4 
.
1.10.5 
.
1.10.6 
.
1.10.7 
.
1.10.8 
.
1.10.9 
.
1.10.10 
.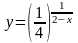