25. Как производиться сглаживание траектории в пространстве присоединенных переменных?

Планирование сглаженных траекторий в пространстве присоединенных переменных следует проводить с учетом следующих соображений:

1. В момент поднятия объекта манипулирования движение схвата должно быть направлено от объекта;

2. Допустимое движение ухода задается на нормали к поверхности, на которой расположен объект, траектория схвата должна проходить через эту точку.

3. Для участка подхода к заданному конечному положению: схват должен пройти через точку подхода, расположенную на нормали к поверхности, на которую должен быть помещен объект манипулирования.

4. Траектория движения манипулятора должна проходить через четыре заданные точки: начальную точку, точку ухода, точку подхода и конечную точку (рис. 9.2).

5. На траекторию накладываются условия:

   1. начальная точка: заданы скорость и ускорение (обычно нулевые);

   2. точки ухода: непрерывность положения, скорости и ускорения;

   3. точка подхода: непрерывность положения, скорости и ускорения;

   4. конечная точка: заданы скорость и ускорение (обычно нулевые).

6. Значения присоединенных координат должны лежать в пределах физических и геометрических ограничений каждого из сочленений манипулятора.

7. При определении времени движения необходимо учесть:

   1. время прохождения начального и конечного участков траектории выбираются с учетом требуемой скорости подхода и ухода схвата, и представляет собой некоторую константу, зависящую от характеристик силовых приводов сочленений

   2. время движения по среднему участку траектории определяется максимальными значениями присоединенных скоростей и ускорений каждого сочленения.

Рисунок 14.2. Ограничения по положению для траектории в пространстве присоединенных переменных

Для проведения интерполяции траектории по заданным узловым точкам нужно выбрать полиномную функцию степени не выше n.

Например, описание i–го сочленения полиномом седьмой степени:

, (14-1)

в котором неизвестные коэффициенты определяются из заданных граничных условий и условий непрерывности. Однако полином такой высокой степени трудно вычислить. Нужно разбить траекторию движения на несколько участков и интерполировать каждый участок полиномом низкой степени.

Например, траектория изменения каждой присоединенной переменной разбивается на три участка (4-3-4). Первый участок, задающий движение между начальной точкой и точкой ухода, описывается полиномом четвертой степени. Второй (средний) участок – между точкой ухода и точкой подхода – описывается полиномом третьей степени. Последний участок – полиномом четвертой степени.

26. Как производиться планирование траекторий манипулятора в декартовой системе координат? Кратко опишите метод, использующий матрицу однородного преобразования.

Планирование в декартовых координатах

При решении задач планирования в пространстве декартовых координат отдельно решается задача планирования для координат XYZ и отдельно для углов OAT. Рассмотрим для XYZ.

Изменение координат XYZ при движении по прямой будет происходить по следующему закону:

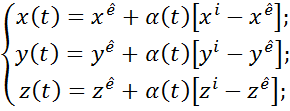
Это параметры уравнения прямой в декартовом пространстве, которое используется для команды GOS.

В этих уравнениях изменяется от единицы до нуля и профиль скорости так же будет состоять из интервалов разгона, движения с постоянной скоростью и торможения.

Параметры и для траектории находят:

и определяют исходя из ограничений на минимум скорости и ускорения схвата манипулятора на траекторию.

Если профиль скорости трапециевидный:

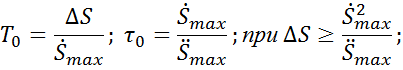
Если профиль скорости треугольный:

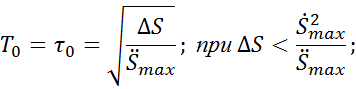
– Путь, пройденный схватом в декартовом пространстве.

– Максимальная линейная скорость схвата.

– Максимальное линейное ускорение схвата.

Значения и вычисляются так же, как и для команды GO.

Матрица однородного преобразования

Она представляет собой матрицу размерностью 4´4, которая преобразует вектор, выраженный в однородных координатах, из одной системы отсчёта в другую.

Однородная матрица преобразования может быть разбита на четыре подматрицы:

Т = =

Верхняя левая подматрица размерностью 3×3 представляет собой матрицу поворота;

верхняя правая подматрица размерностью 3×1 представляет собой вектор положения начала координат повернутой системы отсчета относительно абсолютной;

нижняя левая подматрица размерностью 1×3 задает преобразование перспективы; четвертый диагональный элемент является глобальным масштабирующим множителем.

Однородная матрица преобразования позволяет выявить геометрическую связь между связанной системой отсчёта OUVW и абсолютной системой OXYZ.

Если вектор р трехмерного пространства выражен в однородных координатах, т.е. , то, используя понятие матрицы преобразования, можно сформировать однородную матрицу преобразования Т_пов, задающую преобразование поворота и имеющую размерность 4×4. Однородная матрица поворота получается соответствующим расширением обычной матрицы поворота, имеющей размерность 3×3. Тогда получившиеся матрицы размерностью 4×4 называются однородными матрицами элементарных поворотов. Однородная матрица преобразования переводит вектор, заданный однородными координатами в системе отсчета OUVW, в абсолютную систему координат OXYZ, т.е. при :

.