Экзаменационный билет №_4

Комплексный чертеж плоскости:

а) плоскости общего положения;

б) взаимопринадлежность прямой, точки и плоскости;

в) главные линии плоскости;

г) построение проекций плоских многоугольников ( при n>3)

д) плоскости частного положения

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости 

Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки

Главные линии плоскости — это особые прямые, принадлежащие плоскости и позволяющие более точно выявить ориентацию плоскости в пространстве и упростить решение многих графических задач. К главным линиям плоскости относят линии уровня плоскости и линии наклона плоскости к плоскостям проекций

построение проекций плоских многоугольников . Треугольник всегда является плоской фигурой, чего нельзя сказать про четырехугольник, пятиугольник и т.д., плоскостность которых надо выявлять на чертеже

Проецирующие уровня и их свойства

1. Проекция точки есть точка.

2. Проекцией прямой в общем случае является прямая.

3. Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций

4. Проекцией прямой, параллельной направлению проецирования, является точка.

5. а) Если отрезок параллелен плоскости проекций, то он проецируется на нее в натуральную величину.

б) В противном случае, при прямоугольном параллельном проецировании он имеет проекцию меньшую истиной величины.

6. Если точка принадлежит прямой, то проекция этой точки лежит на проекции этой прямой.

7. Если точка, лежащая на прямой, делит ее на отрезки в каком-либо отношении, то проекция этой точки поделит проекцию этой прямой в том же отношении.

8. Если прямые пересекаются, то их проекции тоже пересекаются. Причем проекция точки пересечения прямых является точкой пересечения проекций.

9. Проекции параллельных прямых параллельны между собой.

Экзаменационный билет №_5

Определение общих элементов простейщих геометрических образов из условий принадлежности:

а) определение точки пересечения прямой с проецирующей плоскостью,

б) определение линии пересечения плоскости общего положения с проецирующей плоскостью и двух проецирующих плоскостей

в) изображение на комплексном чертеже прямой линии, параллельной плоскости и двух параллельных плоскостей.

Пересечение прямой общего положения с плоскостью общего положения (первая основная позиционная задача).

В общем случае задача на пересечение прямой с плоскостью решается с помощью вспомогательной секущей плоскости, на которую накладывается ряд условий:

1) она должна быть плоскостью частного положения;

2) должна проходить через заданную прямую

Общий прием построения линии пересечения двух плоскостей заключается в следующем. Вводят вспомогательную плоскость, строят линии пересечения вспомогательной плоскости с двумя за­данными и в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

 

Для наглядного изображения построения первой общей точки линии пересечения плос-костей P и Q  введена вспомогательная плоскость S.С плоскостью P она пересекается по линии 1-2, с плоскостью Q – по линии 3-4.В пересечении линий 1-2 и 3-4 определена первая общая точка К₁ двух плос­костей

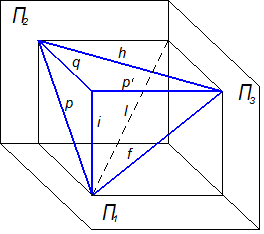
изображение на комплексном чертеже прямой линии. Прямые, наклонённые ко всем плоскостям проекций, называются прямыми общего положения (прямая l). Прямые, перпендикулярные либо параллельные плоскости проекций, называются прямыми частного положения (прямые i, q, p’, h, f, p).

изображение на комплексном чертеже прямой линии, параллельной плоскости и двух параллельных плоскостей. Как и в случае с прямыми линиями различают плоскости общего и частного положения. Плоскости, наклонённые ко всем плоскостям проекций, называются плоскостями общего положения (например, плоскость W). Плоскости, перпендикулярные либо параллельные плоскости проекций, называются плоскостями частного положения (плоскости S, D, Q, Г, Ф, Р).