Экзаменационный билет №_25

Построение разверток призматических и цилиндрических поверхностей.

1. Выполнить комплексный чертеж наклонной треугольной призмы и построить ее развертку;

2. Ответить на следующие вопросы:

а) какие поверхности называются развертывающимися;

б) что называется разверткой;

в) какие поверхности относятся к числу развертывающихся;

г) к чему сводится построение развертки наклонного эллиптического цилиндра.

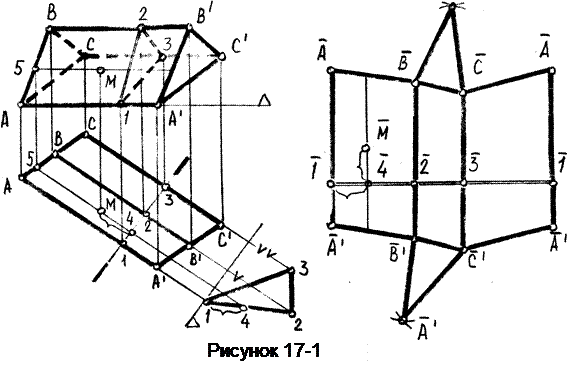
Пример 1. Построить полную развёртку поверхности треугольной призмы и нанести на ней точку М, принадлежащую поверхности.

Призма расположена таким образом, что её боковые ребра являются горизонталями, следовательно на виде сверху они имеют натуральную величину.

Чтобы построить «нормальное» сечение проведём вертикальную плоскость Б перпендикулярно к боковым ребрам призмы. Построим натуру сечения с помощью дополнительного вида, выполненного по направлению горизонтали, перпендикулярной к плоскости Б. Стороны треугольника натурального вида сечения будут являться искомыми высотами параллелограммов.

Т.к. при построении развёртки углы и параллельности сохраняются, то на развёртке боковые ребра будут параллельны между собой и перпендикулярны прямой линии, в которую развернётся «нормальное» сечение.

Построение развёртки начинается с проведения прямой линии, на которой откладываем длины сторон нормального сечения (высоты параллелограммов) 1-2, 2-3, 3-1.

Через концы этих сторон проведём прямые перпендикулярные им. На полученных перпендикулярах отложим отрезки боковых рёбер, измеренные на виде сверху относительно нормального сечения. Соединив между собой полученные точки отрезками прямых, получим развёртку боковой поверхности призмы. Присоединив к этой развёртке оба основания, получим полную развёртку поверхности призмы.

Чтобы построить на развёртке точку М, принадлежащую поверхности призмы, необходимо найти на развёртке положение прямой, на которой эта точка лежит. Для этого найдём точку пересечения этой прямой с плоскостью Б на натуральном виде сечения. Замерим расстояние 1-4 и отложим его на развёртке. Через полученную точку проведём прямую, параллельную ребрам призмы. Затем измерим на виде сверху длину отрезка - от нормального сечения до точки М и отложим его на развёртке.

Экзаменационный билет №_26

1. Линейчатые развертывающиеся поверхности ( торс, коническая, цилиндрическая поверхности).

а) образование;

б) комплексные чертежи;

в) принадлежность точки поверхности.

1. Конические поверхности задаются движением прямой линии l, проходящей через неподвижную точку М, по некоторой направляющей кривой линии а. (рис 128)

2. Цилиндрические поверхности задаются движением прямой, параллельной некоторому направлению, по заданной направляющей кривой. (рис 129)

    

Экзаменационный билет №_27

1. Построение точки пересечения кривой поверхности с прямой линией общего положения

1. Выполнить комплексный чертеж сферы и пересекающей ее прямой общего положения;

2. Определить точки пересечения, видимость прямой и составить алгоритм решения.

3. Ответить на следующие вопросы:

а) к какому типу относится данная задача;

б) по какой схеме решается такого типа задача;

в) какой принцип положен в основу выбора вспомогательной плоскости.

Словесная форма	Графическая форма
Y.1. Заключить данную прямую линию а во вспомогательную плоскость Y, a Вспомогательную плоскость следует выбирать так, чтобы в результате получались простейшие сечения (линии, окружности)
2. Определить линию пересечения l вспомогательной плоскости Y с заданной поверхностью, Y∩a– l(1-2-3-4-5-6)
3. Соединить точки полученной линии пересечения с данной линией а, Y∩a-l(1-2-3-4-5-6). 4. Определить видимость прямой линии а