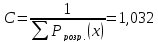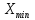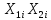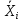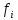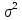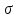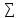8. Визначення основних параметрів.

Таблиця 2.2. Основні параметри:

Параметр	Позначення	Значення
Максимальне		14,73
Мінімальне		-2,07
Кількість даних	n	70
Розмах	R	16,8
Кількість класів	k	7
Ширина класу	h	2.36

9. Побудова варіаційного ряду.

Таблиця 2.3. Варіаційний ряд:

Класи				Cереднє значеняя класу		Частота
-2,5	-	-0,01	-1,255		4
0	-	2,49	1,245		11
2,5	-	4,99	3,745		20
5	-	7,49	6,245		14
7,5	-	9,99	8,745		11
10	-	12,49	10,745		4
12,5	-	15	13,75		6

10. Побудова гістограми.

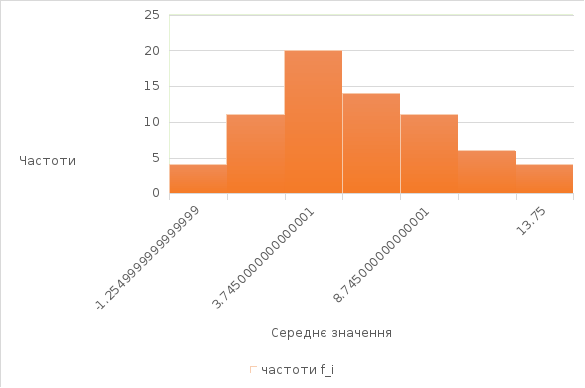
Гістограма 2.1. Значення частот для нормального розподілу.

11. Знаходження додаткових числових характеристик для варіаційного ряду.

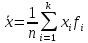
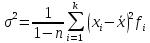
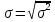
Таблиця 2.4. Додаткові характеристики:

Характеристика	Позначення	Значення
Середнє значення даних		5,412
Дисперсія		15,05
Середнє квадратичне відхилення		3,88

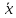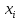12. Знаходимо розрахункові значення для функції розподілу Р(х) за формулою «Нормальний розподіл», підставивши в неї значення середнього арифметичного , значення , відхилення 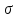при інтегральному значенні «ИСТИНА» Отриманні значення для Х1 віднімемо від значень отриманих для Х2.

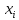13. Також знаходимо розрахункові значення для розподілу імовірностей р(х) за формулою «Нормальний розподіл», підставивши в неї значення середнього арифметичного , значення , відхилення при інтегральному значенні «ЛОЖЬ».

14. Будуємо таблицю за пунктами 12 та 13.

Таблиця 2.5. Функція і розподіл імовірності:

"ИСТИНА"				"ЛОЖЬ"
Р(Х1)	P(X2)	Р(Х1)	P(X2)
0,020704	0,081116	0,06041259	0,023487029
0,081504	0,225665	0,144160829	0,057756528
0,22644	0,456682	0,230241728	0,093762932
0,457704	0,703885	0,2461803	0,100488968
0,704775	0,881002	0,176226764	0,07109887
0,881513	0,965955	0,084441612	0,033209636
0,966149	0,993271	0,027121291	0,010212217
		0,968785114

15. Знаходимо нормований коефіціент с за допомогою формули: