
- •Общий курс физики Учебно-методическое пособие к решению задач и выполнению контрольных работ по физике для студентов заочного обучения
- •Введение
- •1. Общие методические указания
- •Самостоятельная работа по учебным пособиям
- •Решение задач
- •Выполнение контрольных работ
- •Астраханский инженерно – строительный институт
- •Заочное отделение контрольная работа №
- •Результаты проверки
- •Рабочая программа по физике физические основы классической механики
- •Молекулярная физика и термодинамика
- •Электричество и магнетизм
- •Геометрическая оптика (техническая оптика)
- •Колебания и волны
- •Квантовая механика
- •Порядок выполнения контрольных работ
- •Контрольные задания для студентов, обучающихся по направлению подготовки «Прикладная геодезия»
- •Контрольная работа № 2 «Электростатика, постоянный ток, электромагнетизм»
- •Контрольная работа №3 «Техническая оптика»
- •Контрольная работа №4 «Волновая оптика, квантовая физика, физика атома и атомного ядра»
- •Контрольная работа № 2 «Электростатика, постоянный ток, электромагнетизм»
- •Контрольная работа №3 «Волновая оптика, квантовая физика, физика атома и атомного ядра»
- •Контрольная работа №1 (по выбору) «Геометрическая оптика. Основы оптики»
- •2. Физические основы классической механики
- •2.1. Основные формулы и понятия Кинематика материальной точки твердого тела
- •Основные виды прямолинейного движения:
- •Динамика материальной точки и твердого тела
- •Силы в природе:
- •1. Сила гравитации
- •2. Сила тяжести
- •3. Вес тела
- •4. Сила реакции опоры
- •5. Сила упругости
- •6. Сила трения
- •Динамика вращательного движения твердого тела
- •Релятивистская механика
- •Некоторые рекомендации при решении задач по кинематике
- •Некоторые рекомендации при решении задач по динамике
- •2.2. Примеры решения задач
- •2.3. Задачи для самостоятельного решения
- •3. Молекулярная физика и термодинамика
- •3.1. Основные формулы и понятия
- •2. Изобарный процесс.
- •3. Изохорический процесс.
- •3.2. Примеры решения задач
- •3.3. Задачи для самостоятельного решения
- •4. Электростатика. Постоянный электрический ток
- •4.1. Основные формулы и понятия
- •4.2. Примеры решения задач
- •Подставляя выражения (6) в (5), получим
- •4.3. Задачи для самостоятельного решения
- •5. Электромагнетизм. Колебания
- •5.1. Основные формулы и понятия
- •Напряженность магнитного поля в центре кругового тока (рис.5.3.)
- •Напряженность магнитного поля на оси кругового тока (рис.5.6.)
- •5.2. Примеры решения задач
- •5.3. Задачи для самостоятельного решения
- •6. Геометрическая оптика
- •6.1. Основные формулы и понятия
- •Обратимости светового луча;
- •Постулат Ферма, называемый принципом наименьшего времени:
- •6.2. Примеры решения задач
- •Решение:
- •6.3. Задачи для самостоятельного решения
- •7. Оптика
- •7.1. Основные формулы и понятия Волновая оптика
- •Элементы квантовой оптики
- •7.2. Примеры решения задач
- •7.3. Задачи для самостоятельного решения
- •8. Квантовая механика. Основы атомной и ядерной физики
- •8.1. Основные формулы и понятия Квантовая механика
- •Атомная физика
- •Физика твердого тела
- •8.2. Примеры решения задач
- •8.3. Задачи для самостоятельного решения
- •Приложения
- •Список использованной литературы
3.2. Примеры решения задач
Задача 3.1. Определить молярную массу смеси кислорода массой m1 = 25 г и азота массой m2 = 75 г.
Дано: m1 = 25 г = 25·10-3 кг m2 = 75 г = 75·10-3 кг |
Решение: Молярная масса смеси М есть отношение массы смеси m к количеству вещества смеси ν:
Масса смеси равна сумме масс компонентов:
|
Найти: М = ? |
Количество вещества смеси равно сумме количества компонентов:
![]() .
(3)
.
(3)
Подставив в формулу (1) выражения (2) и (3) и преобразовав, получим:
![]() .
.
Молярные массы кислорода М1 и азота М2 определяем из таблицы Менделеева:
М1=32·10-3 кг/моль и М2=28·10-3 кг/моль
Вычисления:
![]() .
.
Ответ:
![]()
Задача 3.2. Два баллона соединены трубкой с закрытым клапаном, объемом которой можно пренебречь. В баллоне объемом 0,02 м3 находится газ под давлением 1,6×104 Па, а в баллоне объемом 0,06 м3 - тот же газ под давлением 1,2×104 Па. Какое давление установится в баллонах, если открыть кран? Температура газа остается постоянной.
Дано:
V1 = 0,02 м3 р1 = 1,6×104 Па V2 = 0,06 м3 р2 = 1,2×104 Па Т = const.
|
Решение: Газ занимает весь предоставленный ему объем. После того, как клапан будет открыт, часть газа из одного сосуда будет переходить в другой до тех пор, пока давление в обоих сосудах не уравняется. Объем, который будет занимать газы, равен сумме объемов сосудов V = V1 + V2, где V1 - объем первого сосуда, V2 - объем второго сосуда. Давление, установившееся в сосудах, согласно закону Дальтона, р = р1' + р2' (1) |
Найти:
р - ?
|
где р1' - давление газа первого сосуда, р2' - давление газа второго сосуда.
По условию задачи температура газа остается неизменной, следовательно, согласно закону Бойля-Мариотта для двух состояний газа можно записать:
![]() ,
(2)
,
(2)
Решая полученную систему уравнений
![]()
получим
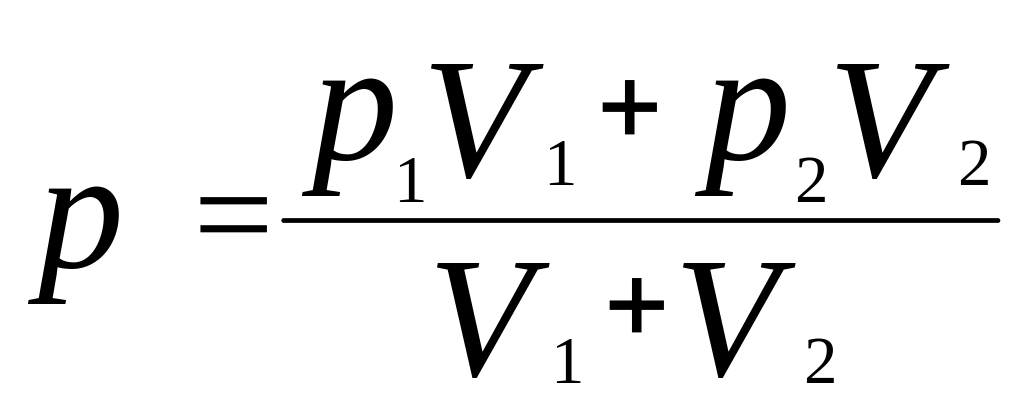
Проверить единицы физических величин слева и справа от знака равенства
![]()
Вычисления:
![]() 1,3×104
Па.
1,3×104
Па.
Ответ: р = 1,3×104 Па.
Задача 3.3. Баллон содержит m1= 80 г кислорода и m2=320 г аргона. Давление смеси р=1 МПа, температура Т=300 К. Принимая данные газы за идеальные, определить объем V баллона.
Дано:
m1 = 80 г=0,08 кг m2 = 320 г=0,32 кг р = 1 МПа =1×106 Па Т = 300 К.
|
Решение:
По уравнению Менделеева - Клайперона, парциальные давления р1 кислорода и р2 аргона выражаются формулами:
где М1 и М2 - молярная масса кислорода и аргона, R=8,31 - универсальная газовая постоянная. |
Найти: V-?
|
По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:
р = р1 + р2 (2)
Подставив уравнение (1) в уравнение (2), получим:
![]() .
.
из последнего выражения найдем объем баллона:
![]() ,
,
где М1=32·10-3 кг/моль – молярная масса кислорода, М2=40·10-3 кг/моль – молярная масса аргона (из таблицы Менделеева).
Вычисления:
![]()
Ответ: V=0,0262 м3
Задача 3.4. Найти
среднюю кинетическую энергию
![]() вращательного движения одной молекулы
кислорода при температуре Т=350 К, а также
кинетическую энергию Ек
вращательного движения всех молекул
кислорода массой m
=4 г.
вращательного движения одной молекулы
кислорода при температуре Т=350 К, а также
кинетическую энергию Ек
вращательного движения всех молекул
кислорода массой m
=4 г.
Дано: m = 4 г = 4·10-3 кг Т = 350 К.
|
Решение: На каждую степень свободы молекулы газа приходится одинаковая средняя энергия:
где k=1,38·10-23 Дж/К - постоянная Больцмана, Т – абсолютная температура. |
Найти:
Ек - ?
|
Так как вращательному движению двухатомной молекулы (молекула кислорода – двухатомная) соответствуют две степени свободы, то средняя энергия вращательного движения молекулы кислорода:
![]()
Кинетическая энергия вращательного движения всех молекул газа:
![]() .
(2)
.
(2)
Число всех молекул газа найдем из формулы количества вещества:
![]() ,
(3)
,
(3)
где NA=6,02·1023моль-1 - число Авогадро, ν - количество вещества, М=32·10-3 кг/моль – молярная масса кислорода.
Подставляя уравнение (3) в формулу (2), получим:
![]() .
.
Вычисления:
![]()
![]()
Ответ:
![]() ,
,
![]()
Задача 3.5. Некоторое количество гелия расширяется: сначала адиабатно, а затем изобарно. Конечная температура газа равна начальной. При адиабатном расширении газ совершил работу, равную 4,5 кДж. Какова работа газа за весь процесс?
Дано:
V2 = 3V1 А12 = 4,5·10-3 Дж р = const Q = 0 Т3 = Т1 |
Решение: Изобразим графически процессы, происходящие с газом.
|
Найти:
А123 - ?
|
На графике процесс 1-2 является адиабатным, т.е Q = 0; процесс 2 – 3 - изобарный (р = const). Так как начальные и конечные температуры равны (по условию задачи), то процесс 3 – 1 будет изотермическим (Т=const).
полная работа равна сумме работ на каждом из участков:
А123 = А12 + А23 (1)
По
первому закону термодинамики для
адиабатного процесса, учитывая, что газ
одноатомный работа А12
газа на участке 1-2, равна изменению
внутренней энергии
![]() ,
взятой со знаком «минус»:
,
взятой со знаком «минус»:
![]() ,
(2)
,
(2)
где М = 4·10-3 кг/моль – молярная масса гелия, Т1 и Т2 – абсолютные температуры газа в состоянии 1 и 2 соответственно, R=8,31 - универсальная газовая постоянная.
Работа изобарного расширения, учитывая, что Т3 = Т1, равна
![]() .
(3)
.
(3)
Решая совместно полученные уравнения
А123 = А12 + А23
![]()
![]()
Получим
А123
=
![]() А12.
А12.
Вычисления:
А123 = ·4,5·103=7500 Дж
Ответ: А123 = 7500 Дж.
Задача 3.6. Коэффициент диффузии D и вязкость η водорода при некоторых условиях равны D = 1,42·10-4 м2/с и η = 8,5 мкПа·с. Диаметр молекул водорода σ = 0,3 нм. Найти число n молекул водорода в единице объема.
Дано: D = 1,42·10-4 м2/с η = 8,5 ·10-6 Па·с σ = 0,3·10-9 м
|
Решение: Коэффициент диффузии D и коэффициент вязкости η, определяются уравнениями:
где
|
Найти: n - ? |
![]() -
средняя длина свободного пробега
молекул; ρ – плотность газа.
-
средняя длина свободного пробега
молекул; ρ – плотность газа.
Количество вещества:
![]() ,
,
где М=2·10-3 кг/моль – молярная масса водорода; m – масса газа; NA=6,02·1023 моль-1 - число Авогадро, ν - количество вещества.
Концентрация молекул водорода n определяется числом молекул N в единице объема V:
![]()
Решая совместно систему уравнений:
![]()
можно получить:
![]()
Вычисления:
![]() м-3
м-3
Ответ: n = 1,8·1025 м-3
задача 3.7. Тепловая машина работает по обратимому циклу Карно. Температура теплоотдатчика Т1 = 500 К. Определить термический КПД цикла и температуру Т2 теплоприёмника тепловой машины, если за счёт каждого килоджоуля теплоты, полученной от теплоотдатчика, машина совершает работу А= 350 Дж.
Дано:
А= 350 Дж Q1 = 1кДж=103 Дж Т1=500 К |
решение: Термический КПД тепловой машины показывает, какая доля теплоты, полученной от теплоотдачика, превращается в механическую работу. Термический КПД выражается формулой:
где Q1 - теплота, полученная от теплоотдачика, А – работа, совершенная рабочим телом тепловой машины |
Найти: η-? Т2-? |
Зная КПД цикла, можно из формулы для КПД цикла Карно
![]()
найти температуру охладителя Т2:
![]() .
.
Вычисления:
![]()
![]()
Ответ: η=35%, Т2=325 К
Задача 3.8. Масса 10 г гелия находится при температуре 300 К. При изобарном нагревании его объем увеличился в 3 раза. Определить изменение внутренней энергии, работу газа и количество теплоты, сообщенное газу.
Дано: m = 10×10-3 кг М = 4×10-3 кг/моль Т1 = 300 К V2 = 3V1 P = сonst. |
Решение:
Изменение внутренней энергии газа можно найти, используя уравнение:
где R=8,31 Дж/(К·моль) – универсальная газовая постоянная; М – молярная масса газа; m – масса газа; Т1 и Т2 – абсолютные температуры начального и конечного состояния газа. |
Найти: DU = ? A = ? Q = ?
|
Для определения температуры T2 воспользуемся законом Гей-Люссака для изобарического процесса
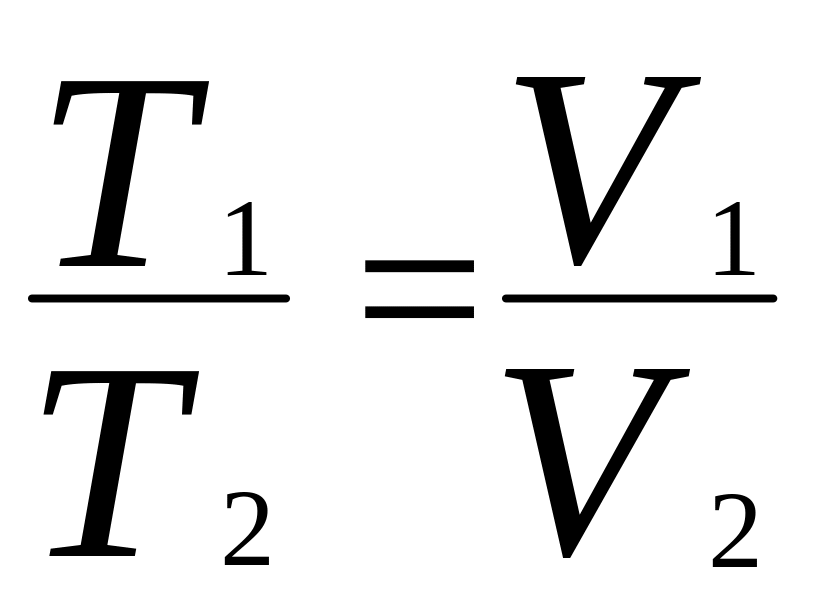
откуда
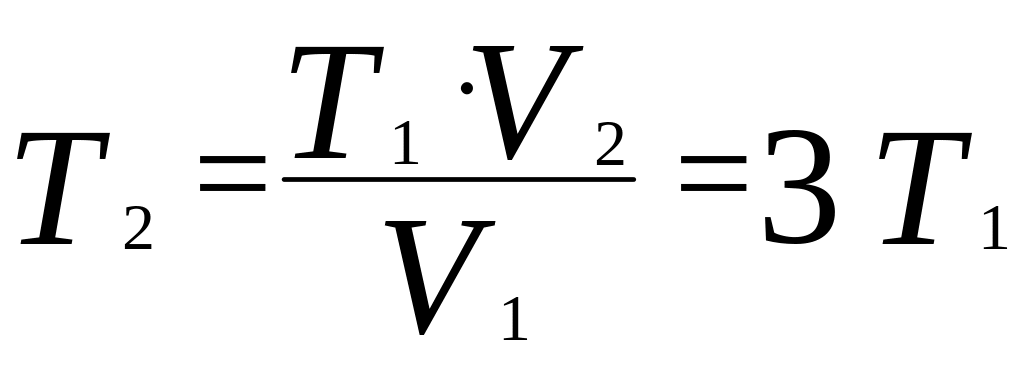
Тогда
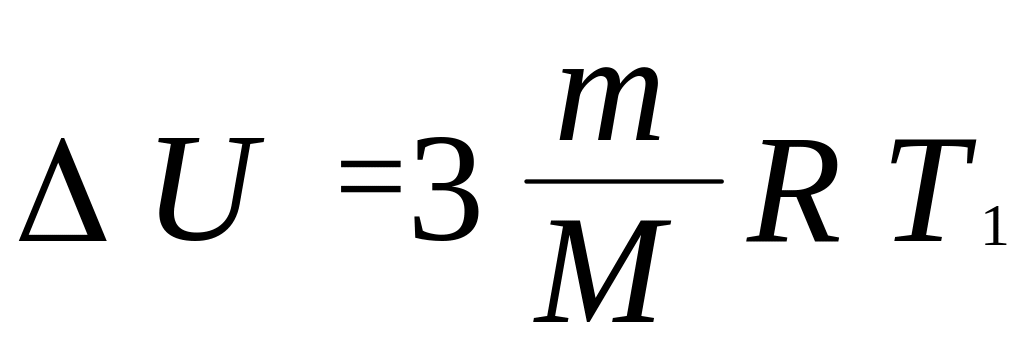 .
.
Работа газа при его расширении определяется выражением:
А = PV = P(V2 - V1). |
Воспользовавшись уравнением Менделеева-Клайперона, найдем разность объемов двух состояний газа (V2 – V1):
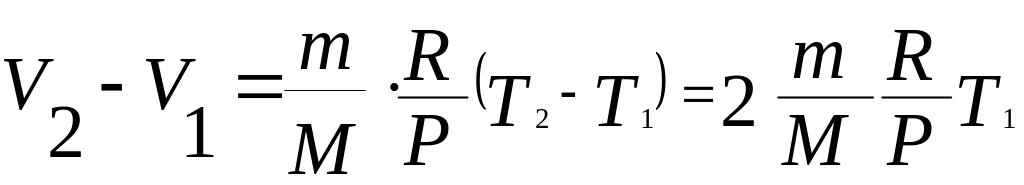 .
.
Тогда
 .
.
Для определения количества теплоты, сообщенной газу, воспользуемся первым законом термодинамики для изобарического процесса:
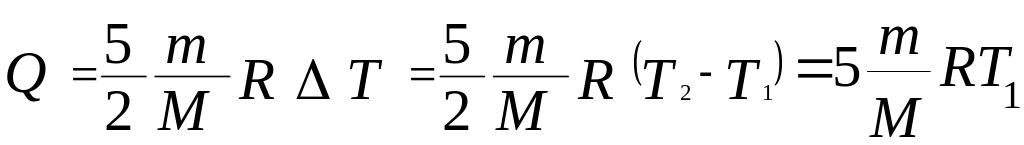
Вычисления:

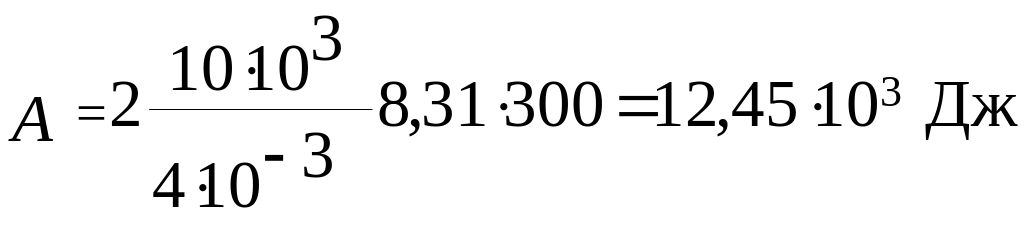
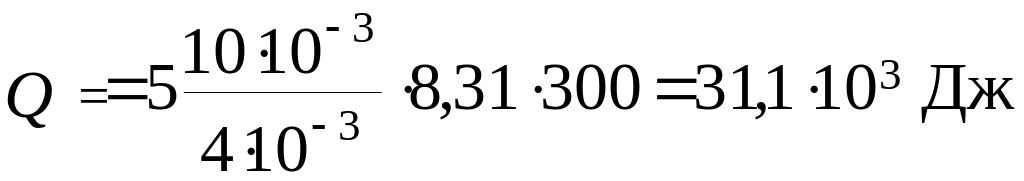
Ответ: U = 18,7·103 Дж; А = 12,45·103 Дж; Q = 31,1·103 Дж.
Задача 3.9. Газовая смесь состоит из азота массой m1=2 кг и аргона массой m2 = 1 кг. Принимая данные газы за идеальные, определить удельные теплоемкости сV и сP газовой смеси.
Дано: m1 = 2 кг m2 = 1 кг |
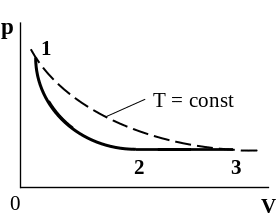
Решение: Количество теплоты, необходимое для нагревания смеси аргона и азота найдем двумя способами:
где сV – удельная теплоемкость смеси газов при постоянном объеме; сV1 - удельная теплоемкость азота при постоянном объеме; сV2 - удельная теплоемкость аргона при постоянном объеме. |
Найти: сV - ? сP - ? |
Приравнивая правые части уравнений (1) и (2) и произведя сокращения, получим

откуда
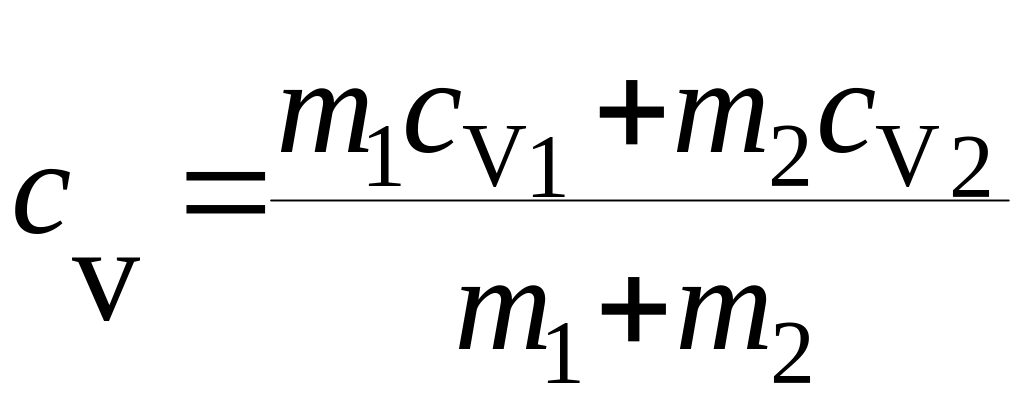 .
(3)
.
(3)
Аналогично найдем выражение для сР :
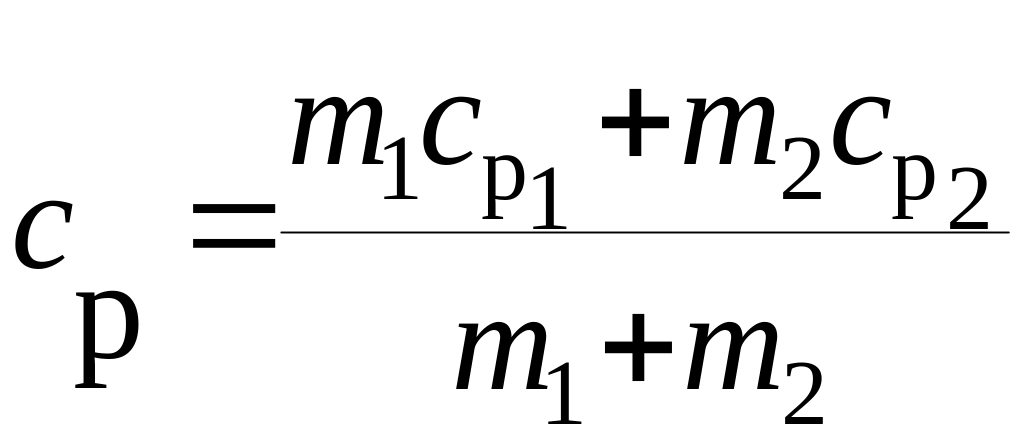 .
(4)
.
(4)
Удельные теплоемкости идеальных газов при постоянном объеме сV и постоянном давлении сР выражаются формулами:
![]() (5)
(5)
![]()
где i – число степеней свободы (для двухатомного газа (азот) i=5, для одноатомного (аргон) i=3); R=8,31 - универсальная газовая постоянная; М1 = 28×10-3 кг/моль – молярная масса азота; М2 = 40×10-3 кг/моль – молярная масса аргона.
Подставляя уравнения (5) в формулы (3) и (4), получим
![]()
![]() .
.
Вычисления:
![]()
![]()
Ответ:
![]() ;
;
![]()

 ,
,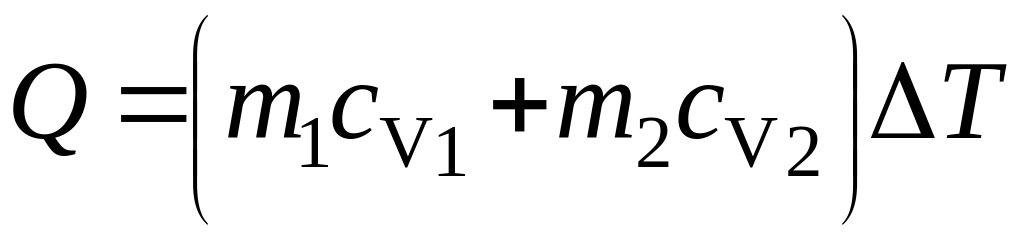 ,
(2)
,
(2)