Теплопроводность однослойной шаровой стенки

На практике такая задача встречается, например, при расчете потерь теплоты через свод высокотемпературной цилиндрической печи с шаровой потолочной частью или в газгольдерах.

Выделим в шаровой стенке элементарный слой dr. Из закона Фурье следует, что

, Вт.

Разделяя переменные и выполняя интегрирование, получим:

;

.

Из граничных условий r=r₁, T=T₁ и r=r₂, T=T₂, найдем:

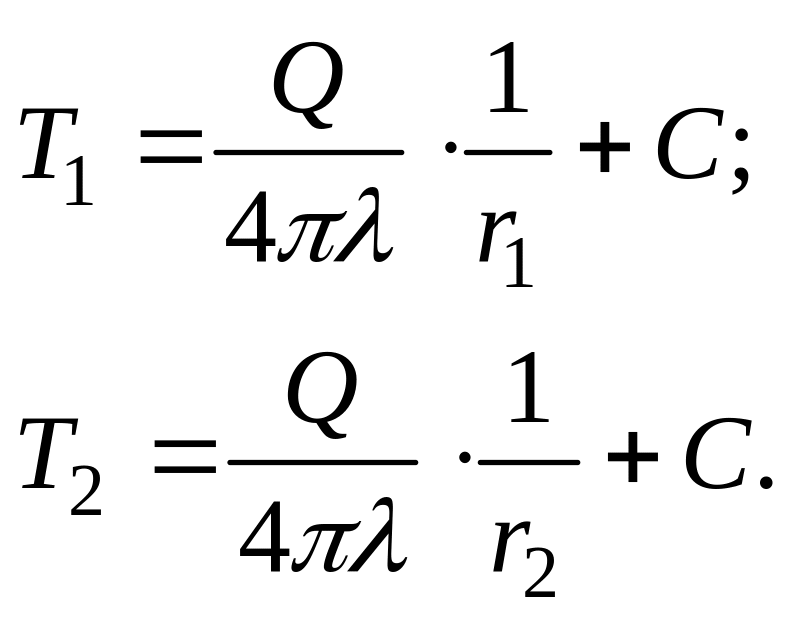
Вычтя из первого уравнения второе, получим:

из последней формулы окончательно имеем:

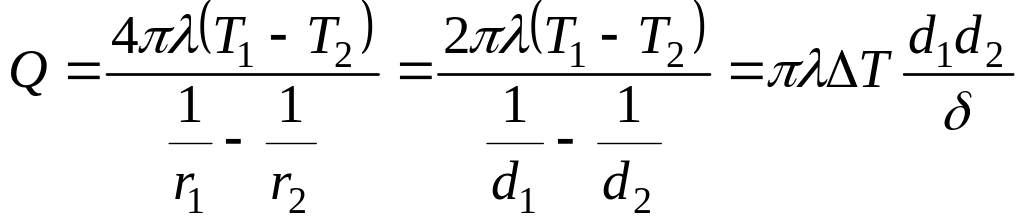, Вт,

где .

Найдя С и Q, получим зависимость температуры от текущего диаметра однослойной шаровой стенки:

,

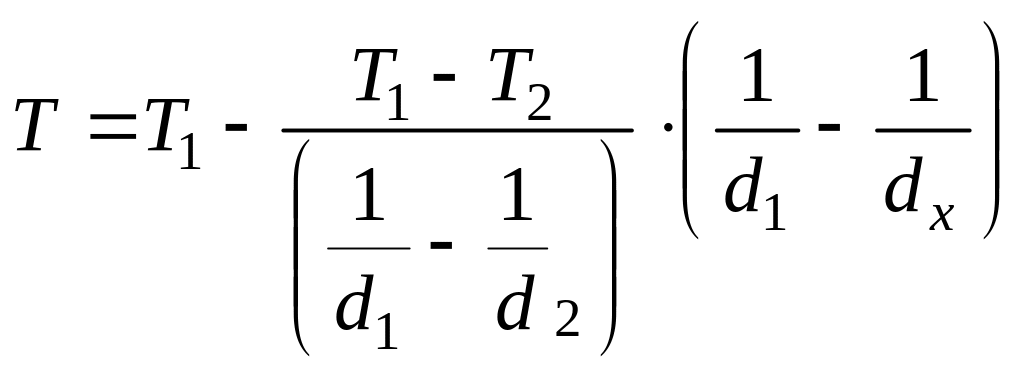где T - температура в любой точке участка .

С учетом зависимости последняя формула примет вид

.

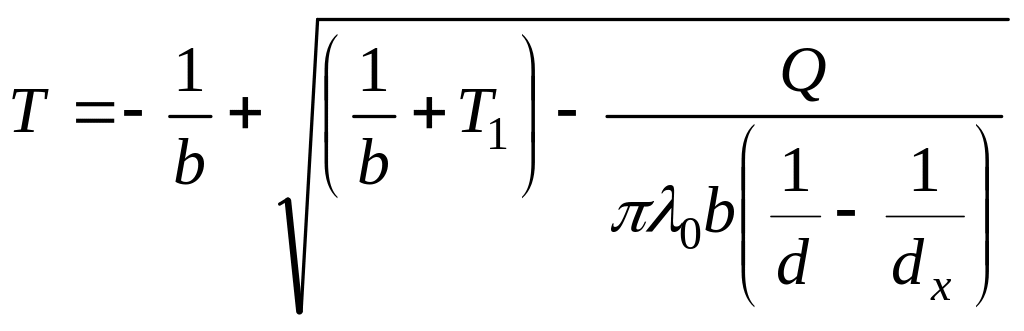Последняя формула указывает на гиперболическое распределение температуры в шаровой стенке.

Часть3. Теплопередача Поток теплоты путем теплопередачи при сложном теплообмене

Теплообмен между двумя жидкими или газообразными средами, разделенными твердой стенкой, или через поверхность раздела между ними называется теплопередачей. Перенос теплоты от теплоносителя к стенке и от стенки к теплоносителю может иметь как конвективный, так и радиационный характер.

При сложном теплообмене поток теплоты можно рассчитать по формуле

.

В формуле для теплового потока - эффективное значение коэффициента теплоотдачи.

,

где и - коэффициенты теплоотдачи конвекцией и тепловым излучением соответственно.

Интенсивность теплопередачи характеризуется коэффициентом теплопередачи k, Вт/(м²∙К), который определяется как тепловой поток Q, передаваемый через единицу площади F стенки при единичной разности температур сред

.

Теплопередача через плоскую стенку

задача о теплопередаче через плоскую (одно- и многослойную) стенку встречается часто. На рис. приведена схема такого теплообмена. Слева находится жидкость (капельная или газообразная) с температурой , а справа - с температурой . температуры стенки неизвестны. Значения коэффициентов теплоотдачи заданы. Теплообмен является стационарным (конвекция - теплопроводность - конвекция). В этом случае плотности потока теплоты q от горячей жидкости к поверхности стенки, во всех слоях и от более холодной стенки к холодной жидкости одинаковы:

.

В соответствии с последней формулой можно записать:

Затем находим температурные напоры во всех звеньях схемы теплопередачи и складываем полученные выражения.

Окончательно для плотности потока теплоты от горячей жидкости к холодной через многослойную стенку (n - число слоев стенки) получим выражение:

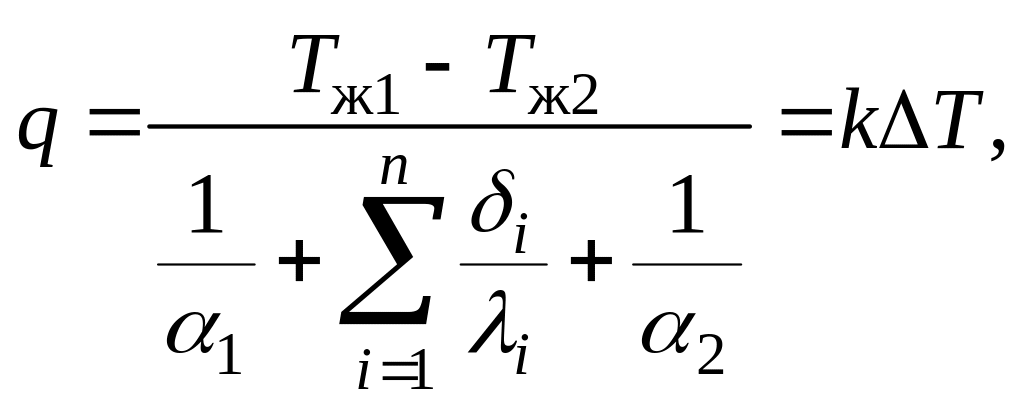Вт/м²,

где 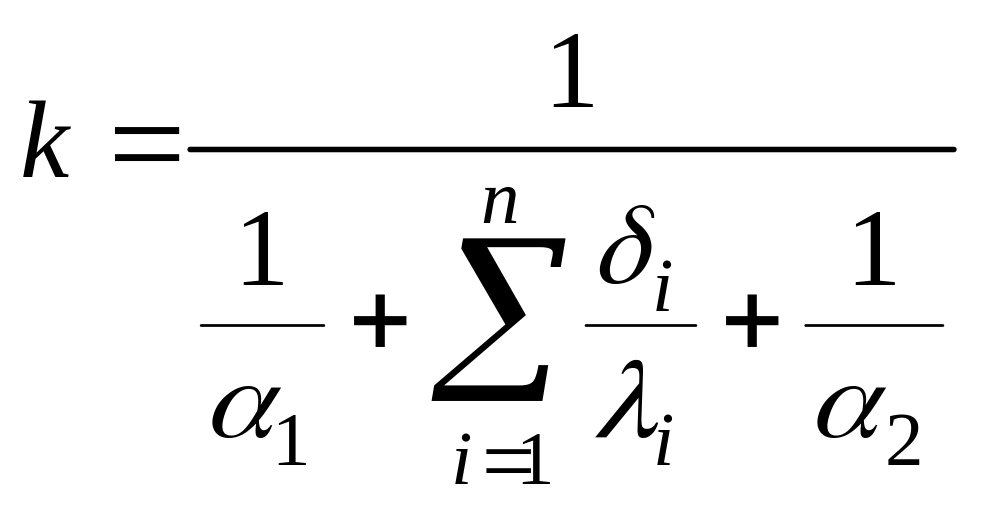- коэффициент теплопередачи.

Величина, обратная (1/k) коэффициенту теплопередачи, называется термическим сопротивлением теплопередаче и обозначается R.

Общим термическим сопротивлением теплопередачи называется величина

.

Общее сопротивление складывается из частных термических сопротивлений теплоотдачи и и термических сопротивлений теплопроводности слоев стенки . Очевидно, что значение R всегда больше, чем наибольшее из значений составляющих ее величин.

Для интенсификации теплопередачи необходимо уменьшить общее сопротивление R. Если частные сопротивления приблизительно одинаковы, то уменьшение любого из них приводит к снижению R в равной степени. если же частные сопротивления заметно отличаются друг от друга, то существенное уменьшение R происходит только при уменьшении наибольшего из них, которое вносит наибольший вклад в сумму.

Очевидно, что для уменьшения теплопотерь необходимо увеличить общее термическое сопротивление.

Теплопередача через однослойную плоскую стенку

Теплопередача через трехслойную плоскую стенку