Дифференциальное уравнение переноса тепла

Предположим, что существует пространство, в котором осуществляется перенос тепла. Выберем точку М. Эту точку окружает контур поверхностью F и объемом V . Через F₁ обозначим поверхность контура, через которую в него входит тепло плотностью q_1. Через F₂ обозначим поверхность контура, через которую из него выходит тепло плотностью q₂.

Тогда общее количество тепла, что входит в контур можно обозначить через интеграл поверхности F₁, т.е. . Общее количество теплоты, которое выходит из данного контура будет равно:

.

С оотношение разницы между входящим и выходящим потоками тепла к объему, ограниченному данным контуром, когда последний стремится к нулю (поверхность стягивается в точку), равна дивергенции потока тепла в данной точке, т.е.

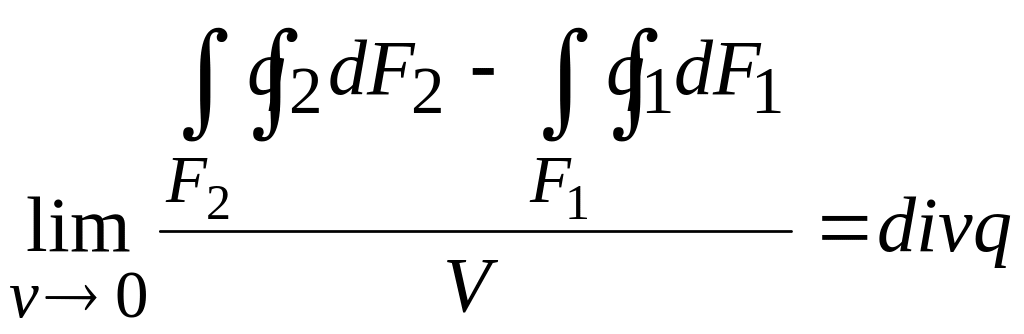. (1.8)

В декартовой системе координат дивергенция обозначается как:

.

Следовательно, для теплового потока дивергенция равна:

, (1.9)

где - являются компонентами вектора плотности теплового потока на координатные оси x, y, z.

В случае, когда количество тепла, которое входит в контур, равно количеству тепла, которое выходит из контура, то div q= 0. В этом случае мы имеем дело со стационарным процессом.

(вспомогательная задача)

В трехмерном случае балансовое уравнение имеет вид:

(1.10)

где: с_р – теплоемкость при постоянном давлении, кДж/кг·К;  - плотность среды, кг/м³; - полная производная температуры по времени (или субстанциональная производная, т.е. производная, связанная с движущейся материей), К/с.

Далее будем полагать, что теплофизические величины λ, с_р и  являются постоянными.

Если , то полный дифференциал этой функции принимает вид:

.

Поделив левую и правую части этого уравнения на , получим:

.

Но есть не что иное, как компоненты вектора скорости w на координатные оси x, y, z, т.е. .

Следовательно, полную производную по времени можно записать в ином виде:

. (1.11)

Возвращаясь к уравнению (1.9) и используя уравнение Фурье, можем записать:

(1.12)

(пояснение)

Считая, что , уравнение (1.12) запишем иначе:

. (1.12а)

Подставляя (1.11) и (1.12а) в исходное уравнение (1.10), получим:

.

Поделив обе части на С_р, получим:

. (1.13)

Равенство (1.13) есть дифференциальное уравнение переноса вещества в подвижной среде (уравнение Фурье-Кирхгофа). Член определяет зависимость температуры от времени, то есть характеризует нестационарность процесса. Член зависит от скорости движения среды и определяет конвективную составляющую переноса тепла в системе. В правой части уравнения (1.13) выражение , характеризует молекулярный перенос тепла, т.е. выражает перенос тепла теплопроводностью. Коэффициент температуропроводности , м²/с, характеризует скорость выравнивания температуры в среде.

Если в среде присутствуют источники тепла (например, выделение теплоты в результате джоулева разогрева проводника при прохождении по нему тока) или стоки тепла (например, испарение влаги в результате нагревания), то балансовое уравнение (1.10) принимает вид:

, (1.14)

где q_V – мощность внутреннего источника (стока) тепла, Вт/м³, которая представляет собой количество теплоты, выделяемое (поглощаемое) источниками (стоками) в единицу объема тела за единицу времени.

В итоге окончательно получим:

(1.15)

Выражение (1.15) является дифференциальным уравнением переноса тепла в движущейся среде при наличии внутреннего источника или стока тепла.