Задание 3. Расчет коэффициента упругоемкости пластовой системы

Теоретический материал:

Для определения значения коэффициента сжимаемости горной породы для коллектора, представленного песчаником, можно воспользоваться корреляционной зависимостью Холла-Щелкачева:

(1.16)

Текущую водонасыщенность пласта вблизи скважины можно косвенно определить по данным обводненности продукции скважины по формуле:

(1.17)

где в – текущая водонасыщенность, определяется по формуле:

(1.18)

Исходные данные:

Параметр	Размерность	Значение
Пористость, m	д.е.	0,17
Насыщенность пор связанной водой, Sв	д.е.	0,35
Обводненность скважинной продукции, nв	д.е.	0,2

Порядок расчета:

1. По формуле (1.16) определяется сжимаемость скелета горной породы.

2. Текущую водонасыщенность пласта получаем из формулы (1.17).

3. По формуле (1.17) определяем коэффициент упругоемкости пласта.

Лабораторная работа №2

«Интерпретация результатов исследования на установившихся режимах

в координатах P_заб от Q»

Теоретический материал:

Обработка результатов исследования в координатах P_заб от Q рекомендуется для прямолинейной формы ИЛ, т.е. когда реализуется линейный закон фильтрации.

Индикаторная линия строится по результатам замеров забойного давления P_забi и дебитов Q_i на режимах исследования, включая режим  замер пластового давления P_пл.

В основу обработки индикаторной линии (при линейном законе фильтрации) положено уравнение прямой вида:

, (2.1)

где А – угловой коэффициент графика ИЛ, равный обратной величине  коэффициента продуктивности скважины, МПа/м³/сут;

P_пл – отрезок, отсекаемый ИЛ на оси давления, Мпа.

Обычно коэффициент продуктивности по ИЛ в этих координатах определяется графически.

Как уже было сказано, в данном случае коэффициент продуктивности определится как величина обратная фильтрационному коэффициенту А:

(2.2)

Исходные данные:

Таблица 2.1

Исходные данные для построения индикаторной линии

№	Q, м3/сут	Pзаб, бар
1	20	174.3
2	34	169.0
3	44	148.3
4	70	127.6
5	85	103.9
6	115	73.7

Порядок расчета:

1. На основе данных из таблицы 2.1 построить индикаторную линию в координатах P_заб от Q.

2. Определить значения фильтрационного коэффициента A и P_пл.

3. Определить значения коэффициента продуктивности скважины .

Лабораторная работа №3

«Интерпретация результатов исследования на установившихся режимах

в координатах P от Q»

Теоретический материал:

Обработка индикаторных линий в этих координатах предполагает, что пластовое давление известно и рекомендуется как для прямолинейной, так и криволинейной формы ИЛ. В случае прямой ИЛ установившаяся фильтрация жидкости в пласте описывается зависимостью:

, (3.1)

где P_i = P_пл – P_забi – депрессия на i-том режиме исследования, МПа;

A – фильтрационный коэффициент, обратный коэффициенту продуктивности.

Q_i – дебит скважины на режиме, м³/сут;

Коэффициент продуктивности определяется графически, как величина, обратная фильтрационному коэффициенту А.

Рисунок 3.1 – Обработка индикаторной линии при линейном законе фильтрации в координатах P от Q

Криволинейная форма индикаторной линии скважины работающей с забойным давлением выше давления насыщения обусловлена нарушением линейного закона фильтрации Дарси.

Основными причинами искривления ИЛ при движении однородной жидкости являются:

1. Инерционные сопротивления и переход от ламинарного течения жидкости к турбулентному;

2. Существенная зависимость свойств пласта и жидкости от изменения давления.

Для установления причин искривления ИЛ необходимо перестроить в координатах: P/Q от Q. Индикаторная линия, перестроенная в данных координатах будет иметь один из трех видов, показанных на рисунке 3.2:

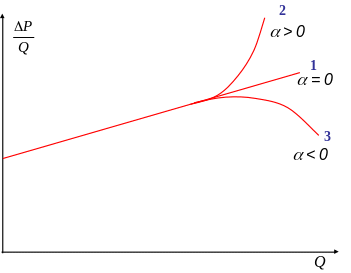
Рисунок 2.2 – Анализ причин нарушения линейного закона фильтрации:

1 – нарушение линейного закона фильтрации за счет инерционных сил;

2 – нарушение линейного закона фильтрации за счет деформации (сжатие трещин) и инерционных сопротивлений;

3 – нарушение линейного закона фильтрации за счет раскрытия трещин и инерционных сопротивлений

Если линия, построенная в данных координатах имеет вид 1 – считают, что нарушение линейного закона фильтрации произошло вследствие возникновения инерционного сопротивления в призабойной зоне скважины. Приток жидкости в этом случае описывается квадратичным уравнением фильтрации:

. (3.2)

В уравнении 2.2 произведение АQ_i равно потерям давления из-за вязкостного трения; BQ_i² – выражает интегральный эффект инерционных сил. При малых значениях В уравнение 3.2 переходит в уравнение 3.1.

Для удобства обработки левую и правую часть уравнения (3.2) необходимо разделить на Q_i, преобразовав его тем самым к уравнению прямой в координатах P/Q от Q:

(3.3)

Коэффициенты A и B определяются по графику, построенному в координатах P/Q от Q:

A – численно равен отрезку, отсекаемому ИЛ на оси ординат;

B – численно равен тангенсу угла наклона ИЛ.

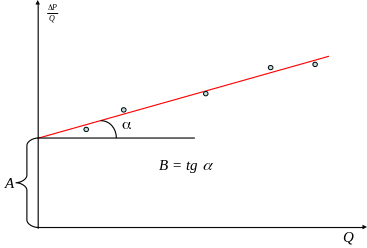
Рисунок 2.3 – Обработка индикаторной линии при квадратичном законе фильтрации.

Ввиду криволинейного характера ИЛ коэффициент продуктивности (приемистости) является величиной переменной с ростом депрессии (репрессии) на пласт. Численно коэффициент продуктивности  равен тангенсу угла наклона хорды, проведенной из начала координат к точке ИЛ, характеризующей работу скважины на рассматриваемом режиме и выражается зависимостью:

. (3.4)

Максимальное значение коэффициент продуктивности принимает в начале координатной линии:

. (3.5)

Если перестроенная ИЛ в координатах P/Q от Q имеет начальный прямолинейный участок, а в конце искривлена вверх, в случае добывающей (см. рисунок 3.2, линия 2), или вниз, в случае нагнетательной скважины (см. рисунок 3.2 линия 3), то нарушение линейного закона фильтрации происходит как вследствие деформационных изменений, так и за счет сил инерции.

Установившийся приток жидкости к скважине в деформируемом пласте при наличии инерционных сопротивлений течению описывается зависимостью:

, (3.6)

где _сi – учитывает дополнительные сопротивления, возникающие вследствие деформации коллектора.

Для случая добывающей скважины функцию вычисляют по формуле:

, (3.7)

Для нагнетательной соответственно:

, (3.8)

где  – параметр деформации, 1/МПа; для добывающей скважины  > 0, а для нагнетательной  < 0.

Коэффициенты , А и В определяются следующим образом. Сначала определяют параметр . Для этого на ИЛ в координатах P от Q берут три точки. Причем точки выбирают так: одну в конце ИЛ, а две другие таким образом, чтобы ИЛ была разделена ими на три, примерно равные части (см. рисунок 3.4).

Рисунок 3.4 – Выбор точек для определения параметра деформации.

Затем определяют по зависимости:

, (3.9)

где

(3.10)

Далее, для каждой величины P_i, соответствующей режиму исследования скважины, определяют функцию _сi по уравнениям (3.7) или (3.8).

Также как для квадратичного режима фильтрации, исходное уравнение (3.6) преобразуют к виду прямой в координатах _с/Q от Q:

(3.11)

Рассчитав для каждого режима значения _сi/Qi, перестраивают ИЛ в координатах _с/Q от Q и стандартным способом находят коэффициенты уравнения А и В, см. рисунок 3.5.

Рисунок 3.5 – Обработка индикаторной линии с учетом деформации коллектора

Если в координатах _с/Q от Q перестроенная ИЛ горизонтальная, то коэффициент B = 0, и нарушение линейной фильтрации происходит только в результате деформационных изменений.

Коэффициент продуктивности (приемистости) скважины для каждого режима работы скважины выражается зависимостью:

, (3.12)

где знак «» берется в случае добывающей скважины, а «+» – нагнетательной.

Как и для квадратичного закона фильтрации, очевидно, Максимальное значение коэффициент продуктивности принимает в начале координатной линии:

(3.13)

Исходные данные:

Таблица 3.1

Исходные данные для построения индикаторной линии

№	Q, м3/сут	P, бар
1	14	31.8
2	21	56.1
3	30	95.5
4	40	145.7
5	52	217.2
6	67	333.6

Порядок расчета:

1. Построить индикаторную линию в координатах P от Q.

2. Если построенная ИЛ соответствует линейному закону фильтрации – провести обработку согласно уравнению фильтрации (2.1). Если ИЛ криволинейна – провести анализ причин нарушения линейного закона фильтрации (см. рисунок 3.2)

3. При квадратичном законе фильтрации провести обработку ИЛ в соответствии с формулой (3.2).

4. При наличии влияния деформации коллектора провести обработку ИЛ в соответствии с формулой (3.6).

5. Определить коэффициент продуктивности скважины (в случае нарушения линейного закона фильтрации определить коэффициенты продуктивности для каждого режима).

Лабораторная работа 4

«Обработка КВД без учета притока»

Для определения метода обработки КВД без учета притока проверяется выполнение условия следующего вида:

(4.1)

где T – время работы скважины на установившемся режиме перед остановкой;

d – максимальная погрешность в д.е. определения асимптоты (конечного прямолинейного участка) и, соответственно, параметров пласта;

t_КВД – общее время снятия кривой восстановления давления

Если условие выполняется, то применяется метода «Касательной», если не выполняется – метод «Хорнера».

Например, если задаться погрешностью определения асимптоты 10%, то для использования метода касательной время работы скважины на режиме перед остановкой скважины T должно быть больше или равно 9·t_КВД.