5.5. Скорости волокон, площадей, объемов
Опять рассмотрим четырехугольник, но бесконечно маленький
– скорость движения
конца вектора
относительно его начала.
Из четырехугольника получаем:
откуда
Полезно проследить цепочку равенств
Здесь учтено, что
и
.
То есть из последнего равенства видно, что операции d/dt и x коммутативны. Очевидно, к операциям r и d/dt это не относится, поскольку не зависящий от времени параметр, в отличие от – если иметь в виду материальную частицу, а не точку пространства. Именно это мы все время имеем в виду, в рамках подхода Эйлера, как и Лагранжа.
В частности, скорость тензора Якоби (или как мы его назвали тензор дисторсии)
Поскольку D=F-I,
,
а
и
,что
впрочем сразу следует из
.
Таким образом,
тензоры Y
и
представляют операторы линейной функции
относительной скорости концов волокна
d
от двух разных аргументов: текущего и
начального положения волокна.
Чтобы найти скорость тензора R, обратного тензору Якоби, можно воспользоваться полученным результатом и свойством обратности:
Учитывая , что Dr=I-R, получим еще одно выражение
Интересно получение (и результат) выражения для скорости Якобиана J. Представим тензор Якоби с помощью его левых проекций в декартовом базисе
;
то же можно сделать и для его скорости
.
Последнее выражение дает смысл левых проекций тензора скорости дисторсии:
,
т.е.
– градиент к-й проекции скорости
.
Поскольку
можно записать
и, например, для первого слагаемого
поскольку
[aab]=[aba]=0.
Аналогичные выражения получим и для остальных слагаемых и, в итоге,
Интересно было бы проделать аналогичные действия с правыми проекциями – можно получить новое полезное выражение. Но этого никто не показывал.
Найдем скорость изменения объема dV
т.е. получили
дивергенцию поля
.
Таким образом, в подходе Лагранжа
Эйлера –
Наконец, с какой скоростью меняется площадь?
Дифференцируем по времени
5. Скорость деформации и вихрь.
Рассмотрим более подробно поле тензора
в некоторый момент времени t.
Будем говорить о мгновенном состоянии
движения, полагая известным поле
скоростей
(1)
и, соответственно, поле градиента
(2)
Напомним, что последний характеризует относительную скорость двух точек (точнее, одной В – относительно А).
А 
В 
Таким образом, относительная скорость - линейная функция с оператором y; последний позволяет найти относительные скорости всех точек в окрестности точки а (точки ).
Разделим тензор Y на симметричную и кососимметричную части
(3)
эти части играют принципиально разную роль.
Скорость (относительная)
имеет два слагаемых
. (4)
Рассмотрим относительно простую ситуацию, когда в некоторой точке поля S=0, тензор Y кососимметричен. Он имеет в декартовом базисе только три независимых компонента и, таким образом, однозначно характеризуется некоторым вектором.
Соответствующие общие формулы (мы их проходили) :
, (5)
причём
. (6)
В нашем случае
и
. (7)
Введём полезный далее вектор
(8)
(пол ротора
);
тогда
,
(9)
Итак, мы собрались рассмотреть ситуацию,
когда
(10)
-независимо от длины и направления .
Очевидно, что этот случай отвечает
вращению окрестности точки
как жёсткого целого со скоростью
.
Поэтому вектор
называют вихрем скорости, а тензор
- тензором завихренности (Мейз).
Соответственно, линии тока для поля
называют вихревыми линиями.
Итак, если Y=K, то происходит вращение. Прагер на этом не останавливается и доказывает обратное: если происходит жёсткое вращение, то S=0.
Рассмотрим два бесконечно коротких
волокна в окрестности точки
,
то есть кроме
возьмём ещё точку
.
При жёстком вращении скорость произведения
равна нулю.
Вычислим
(11)
поскольку
и
- произвольные ненулевые материальные
волокна, то условию
отвечает S=0.
Отсюда следует необходимость (достаточность
была рассмотрена выше) Y=K
для жёсткого вращения.
Другая ситуация: Y=S, то есть K=0. Жёсткого вращения нет. Что есть?
Представим величину
как
(
- угол между волокнами,
и
-
длины волокон);
. (12)
Е
сли
обозначить
и сопоставить с (11), то обнаружим, что
содержимое
представляет двойную проекцию S
. (13)
Два частных варианта для выбора
и
:
а.)
,
,
,
и из (13)
. (14)
Э
то
относительная скорость удлинения
волокна, направленного вдоль
.
Эту величину можно (условно) назвать
скоростью линейной деформации. Условность
состоит в том, что, проинтегрировав эту
величину по времени, мы найдём не
удлинение волокна (отнесённое к его
начальной длине), а логарифмическую
деформацию
;
;
(15)
Если удлинение (ускорение)
мало, то
.
Случай б)
- ведёт к выражению
. (16)
Величину
можно назвать скоростью сдвига (также
с некоторой условностью: сдвигом в
теории упругости называют несколько
другую величину, хотя в сопротивлении
материалов – как раз
).
Как для любого симметричного тензора можно найти главные направления (для которых скорость сдвига равна нулю) и построить круги Мора.
Частные случаи
а) Одноосное движение
,
.
;
,
;
S
– главное значение (два других=0)
-
главные направления.
б) Плоское движение
(17)
, (18)
(19)
Любопытен круг Мора: скорость удлинения (относительная) и скорость поворота волокна (абсолютная)
2
1,2 – главные волокна
1
“ Скорость деформации ” – круг Мора
,
.
Пусть
-
направление
.
Из картинки:
(20)
Таким образом, в матрице
,
,
, (21)
,
(22)
,
. (23)
(24)
(25)
(26)
. (27)
(28)
(29)
(30)
круг радиуса
(31)
(32)
(33)
Из сопоставления:
(34)
, (35)
-
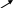
было бы
А
наоборот!
рост
рост
К
Б
руг
Мора-2
А R=0:
(36)
Вращение + расширение
Б R=0,
- вращение (37)
В
(38)