Механика сплошных сред
КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ
Понятие сплошной среды
Д
ля
простоты рассмотрения кинематики
сплошной среды введем пространство, в
котором и будем рассматривать конфигурации.
Пусть имеется абсолютное пространство
и абсолютное время. В таком пространстве
отметим начло отсчета
и радиус-вектор до любой точки этого
пространства будем обозначать
(рис. 1). В данный момент мы будем
рассматривать два произвольных момента
времени t
и t’.
В момент времени t
радиус-вектор до некоторой точки сплошной
среды будем обозначать
,
а в момент времени t’
–
.
Что же такое сплошная среда? В соответствии с определением французского механика Поля Жермена сплошная среда – это система материальных частиц, которая может сильно изменять свою конфигурацию, но при этом оставаться системой. Это определение весьма туманно, но в нем имеется хоть какая-нибудь информация. Следует заметить, что сплошная среда – это система материальных частиц, а не точек. Главным отличием между точкой и частицей состоит в том, что частица может деформироваться, а точка нет, но точка не имеет размеров. В дальнейшем термин частица, как правило, будем заменять на точку, но при этом будем считать, что точка может деформироваться.
Далее Жермен предлагает несколько иное определение сплошной среды. Оно является более определенным, строгим с математической точки зрения, но не более понятным: Семейство множеств St, зависящих от времени t, представляет семейство St – конфигурацией некоторой движущейся кинематической системы S тогда и только тогда, когда при любых t и t’ существует точечное взаимно однозначное отображение множества St’ на множество St, причем совокупность всех отображений образует непрерывную во времени группу (практически эта непрерывная группа определяется в системе пространство-время).
Другими словами: если в абсолютном пространстве R (или системе), которое мы ввели ранее, любая частица задается вектором в произвольный момент времени t, а в момент времени t’ – , тогда
,
где
– это непрерывно дифференцируемая
функция столько раз, сколько нужно.
Здесь можно отметить некоторые свойства этой функции (преобразования).
тождественность
транзитивность
,
т.е. это означает, что к моменту времени
t’
мы можем подойти разными путями: по
прямой из t
в t’
или с заходом в другой момент времени
t’’.если функция изометрична, то St отвечает абсолютно твердому телу, т.е. при движении расстояние между произвольными двумя точками остается неизменным.
и
в моменты времени t’
и t’’
– одна и та же частица если при не
котором t
выполняется условие:
.
Это условие верно при любом t.
Любая точка пространства характеризуется следующими параметрами:
Траектория точки M – это геометрическое место положений Mt в системе отсчета R при переменном t. Аналитически траектория точки записывается в виде:
,
где
и T
фиксировано. Чтобы получить множество
траекторий необходимо варьировать
при постоянном T.Линия истечения (или испускания) для точки в момент времени T – это совокупность точек в момент времени T, которые проходили или пройдут через в различные моменты времени t:
,
где
и T
фиксировано.Скорость частицы – это скорость в момент времени t частицы, которая в момент времени t’ была в точке
:
.
Для удобства записи
вводят функцию
,
где в скобках стоят формальные аргументы.
Тогда скорость частицы определяется
выражением
Ускорение частицы:
.Линия тока – это линии, касательные к которым коллинеарны скоростям
для данного t.
Таким образом, эти линии являются
решением системы дифференциальных
уравнений
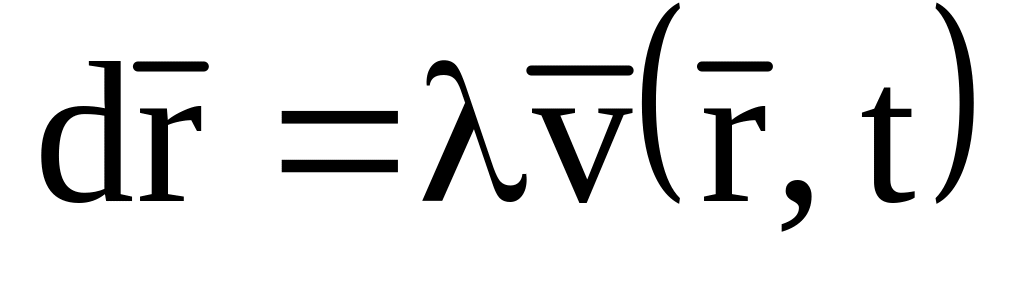или
при фиксированном t.
Другими словами линии тока показывают
как направлены скорости всех частиц в
момент времени t.
Уравнение для траектории частицы имеет
вид:
– интегрируется по времени. Траектория
частицы показывает где находилась одна
точка в каждый момент времени. Линия
тока и траектория точки, как правило,
не совпадают.Стационарное течение. Течение называется стационарным если поле скоростей не зависит от времени T. При этом линии тока определяются независимо от времени t и не меняются со временем. В этом случае траектории частиц, линии тока и линии испускания совпадают.
Подходы Лагранжа и Эйлера
Жермен представил инвариантное описание движение среды в виде вектор-функции трех аргументов. Это описание корректно, но громоздко. Можно использовать более простые функции. Но тогда придется выбирать из двух вариантов, названия которых совпадают с двумя фамилиями, а именно Лагранж и Эйлер.
В данных подходах
вместо пар соответствующих значений
и
в произвольные моменты выбирают
и
,
где под t0
понимается начальный момент времени в
механике твердых деформируемых тел или
произвольный в механике жидкостей и
газов. Но момент t0
не варьируется; достаточно варьировать
только t.
Два подхода отличаются тем, что принять за независимую переменную: или , т.е. положение точки в текущий или начальный момент времени.
Лагранж: принимается положение точки в начальный момент времени, а текущее положение определяется выражением:
Эйлер: за независимую переменную принимается текущее положение точки, тогда начальное положение описывается выражением:
Законы
движения
и
являются взаимно обратными по первому
аргументу. Свойство этих функций –
однозначность (это следует прямо из
определения системы материальных точек
по Жермену). Нам безразлично, когда
запускать часы, и что они в этот момент
показывают, поэтому для удобства будем
считать t0=0.
И естественно имеем
Формально, имея найдем и наоборот. Фактически сделать это обычно непросто, поэтому для решения различных задач выбирают тот или иной подход.
Суть даже не в том, какой функцией пользоваться (или какую получать при решении задачи) – или . Суть в другом: все параметры состояния – напряжения, силы, деформации, скорости, ускорения и т.п. будут рассматриваться как функции : или . Это довольно сильно отличающиеся функции.
Чем удобен подход Лагранжа?
Функция при фиксированных представляет траектории частиц r(t).
При фиксированном
t
представляет поле на множестве
(начальных положений точек), характеризующее
текущее положение точек. Или смещение
точек
Выберем декартовую
систему координат (
)
и вместо векторного поля
рассмотрим три скалярных поля
Сетка поверхностей fi=const.
где были точки,
которые сейчас
лежат на линии
fi=const!
Подход Лагранжа успешно используется в механике при малых смещениях и деформациях: в сопромате, теории упругости, теории пластичности и т.д.
Чем удобен подход Эйлера?
Если зафиксировать
,
то функция
представляет собой совокупность
материальных частиц, проходящих через
в разное время, т.е. функция
представляет собой линию испускания
для некоторой точки пространства
.
Легко заметить, что используемы в сопромате «Вмороженные координаты» является Эйлеровским подходом!.
Смещение в
Эйлеровском подходе определяется как
.
Очевидно, что поля
и
один и тот же вектор, но разный аргумент.
5.3 Изменение элементарных волокон
Положение
или, что то же, смещение u
материальных точек (частиц) в разные
моменты времени обычно нужны для
изучения деформирования среды. Последнее,
как отмечалось ранее, определяется
эволюцией материальных волокон. Как и
раньше, мы будем исследовать эволюцию
прямых волокон, которые можно
характеризовать векторами
.
Но, поскольку прямые волокна в общем
случае искривляются, придется рассматривать
волокна бесконечно малой длины.
Дифференцируемость всех полей означает
«спрявляемость» таких волокон, если их
длины стремятся к нулю.
В подходе Лагранжа
следят за некоторым волокном dx
в окрестности точки x.
Это начальное, недеформированное
состояние; начало волокна в точке
,
а конец в точке
.
Перебирая разные
,
наблюдаем за разными волокнами в этой
окрестности. Обозначим их просто
,
но помним, что речь идет об окрестности
некоторой конкретной точки
.
К моменту t
точка
занимает положение
.
Соседняя – положение
.
Значит бывшее волокно
занимет
положение
.
Тензор
- градиент поля f(
)
в момент t
– линейный оператор, характеризующий
преобразование волокна
в dr.
Раз он линейный, то малая окрестность
точки
,
переходящая в окрестность точки
,
т.е. переезжающая в новое положение на
вектор
(пока мы не рассматриваем развитие во
времени, а только сопоставляем состояние
в два момента: t=0
и t0),
деформируется аффинным образом:
,
т.е. прямые переходят в прямые, параллельные
плоскости – в параллельные, с равными
шагами – остаются с равными шагами. Но
искажаются, как в однородном деформированном
состоянии. Значит,
–
тензор дисторсии F.
Координаты этого тензора
Получаем, что
– направленная производная
поля
.
С другой стороны
это новое положение волокна.
Разложив по базису, получим:
Проекции
столбики,
-
строчки
- по нормали к
поверхности уровня.
Проследим еще раз судьбу волокна.
«Изменение»
– характеризует поворот и деформацию.
Четырехугольник замкнут! Значит, есть
векторное равенство. Удобно взять две
суммы
Раньше было определение тензора дисторсии
.
Сейчас мы видели:
,
т.е.
!
Ну а поскольку
,
то
.
Можно и так посчитать дисторсию.
Возьмем подход Эйлера:
Обозначим:
Dr
– тоже как бы дисторсия, но начало
отсчета – не
,
а
.
Так что это другой тензор, связанный с
D
следующим соотношением
,
т.е.
.
Если взять
,
то получим
.
Произведение
коммутативно! И равно разности между
двумя дисторсиями.
Но брать тензор
надо в соответственных точках!
и
,
и
!
5.4. Изменение элементарного объема
Прежде чем рассматривать изменение элементарных площадей, рассмотрим изменение элементарных объемов. Как потом увидим – это намного проще.
Выделим до деформации (при t=0) элементарный объем в окрестности точки тремя ортогональными векторами
Объем вычисляется следующим образом
где
p
– правизна системы координат.
После деформирования (t0) ребра параллелепипеда занимают положение
Новый объем dV
где p’
– правизна тройки
.
Вспомним некоторые формулы:
и получаем
При малой деформации p’/p=1, J=dV/dV0 – относительное изменение данного элементарного объема . Превращение p’ из 1 в -1 может происходить только через p’=0, когда J=0, т.е. dV=0 ( лежат в одной плоскости). dV при этом превращается в 0! Этого не может быть никогда, т.к. данный феномен означает, что плотность должна возрасти до бесконечности. Значит, J>0 и p’=p.
.
В подходе Эйлера
;
,
но
и т.п.
В соответствующих точках полей и
То же следует из очевидной инверсии
.
Якобиан J входит и в выражение для изменения площадей.
5.5. Изменение элементарных площадей
Пусть
Умножим
и получим
,
т.к.
,
поэтому
и
Тогда
и
.