1. Сызба Геометрия және инженерлік графика пәні. Цилиндирлік бұрама сызықтың эпюрін

Сызба геометрия – геометрияның инженерлер үшiн аса маңызды саласы. Ол түрлi бұйымдардың, физикалық және химиялық құбылыстардың қағаз бетiндегi кескiндерiн тұрғызу заңдылықтарын зерттейдi. Салынған кескiндерiне қарап, бұйымның пiшiнiн және кеңiстiктегi орнын анықтауға, физикалық және химиялық құбылыстарға түсiнуге болады. Осы кескiндердiң көмегiмен бұйымдарға немесе құбылыстарға байланысты мәселелердi талдау ережелерi де сызба геометрияда қарастырылады. Кескiн салынатын қағазды жазықтық деп қарастырады. Сондықтан сызба геометрияда жазықтықтағы кескiндердi салу, кескiндерiне қарап көлемi бар денелердi көз алдымызда елестету және кескiндерде түрлi инженерлiк есептердi шешу теориясы баяндалады.

5. Беттің анықтамасы және жасалуы

Бет деп сызықтардың бiр параметрлiк жиынын айтады. Оны үздiксiз қозғалатын жасаушы деп аталатын сызықтың кеңiстiктегi геометриялық орны ретiнде анықтауға болады. Жасаушы өзiнiң формасын өзгертiп отыруы да мүмкiн. Кейбiр жасаушылары түзу сызықтар болатын қарапайым беттердi келтiрелiк; S нүктесiн және m(Sm) қисығын алып, осы S нүктесi арқылы өтетiн және m қисығымен қиылысатын түзулердiң жиынын қарастыралық (10.2,а-сурет). Осындай түзулердiң бiр параметрлiк жиыны l, l ¹, l ²,…, l ⁱ,… конустық беттi анықтайды. S конустық беттiң төбесi, ал m оның бағыттаушысы деп аталады. Егер n қисығымен қиылысатын және s түзуiне параллель болатын түзулердiң жиыны цилиндрлiк беттi анықтайды /10.2,ә-сурет/. Сонда s түзуi – цилиндрлiк бет жасаушыларын бағытын көрсетедi екен, ал n – оның бағыттаушысы болады. Ендi кеңiстiк қисығын алып, оған жүргiзiлген жанамалар да бiр параметрлiк жиын, яғни бет жасайтынын байқаймыз.

6.2-сурет

Атап айтқанда  қисығына жүргiзiлген жанамалар l, l ₁, l ₂,… торс деп аталатын беттi анықтайды (6.2,б-сурет).

6. Беттің анықтауышы.Анықтауыштың геометриялық және алгоритмдік бөліктері.

Беттi анықтайтын шарттарды беттiң анықтауышы деп атауға келiсiлген. Анықтауыш – геометриялық және алгоритмдiк деп аталатын екi бөлiктен тұрады. Сызба геометрияның керi есебiн шешуге мүмкiндiк беретiн кескiндердi қайтымды деп атайды. Бiр проекциядан тұратын кескiн кайтымды бола алмайды. Сызба геометрияда қарастырылатын қайтымды кескiндерге аксонометрия, монж эпюрi, перспектива және сандық белгiлерi бар проекциялар жатады.

7. Қисықтың қиюшысы мен жанамасы.Қисықтың реті.

Қисық сызық (қысқаша – қисық) деп нүктелердiң бiр параметрлiк жиынын айтады. Оны кеңiстiкте үздiксiз қозғалатын нүктенiң траекториясы ретiнде қарастыруға болады.Қисықты оның проекциясына қарап зерттеймiз. Сондықтан оны проекциялағанда қандай қасиеттердiң сақталатынын бiлудiң үлкен маңызы бар. Егер нүкте сызыққа тиiстi болса, онда осы нүктенiң проекциясы сол сызықтың проекциясына тиiстi болады. Олай болса қисықтың қиюшысы - сол сызық проекциясының қиюшысына, ал жанамасы – жанамасына проекцияланады. Теңдеулерiне қарап қисықтарды алгебралық және трансценденттiк деп ажыратады. Мысалы эллипс (парабола немесе гипербола) – алгебралық қисық, ал синусоида- трансценденттiк қисық екенi түсiнiктi. Алгебралық қисықтың ретi деп оның түзумен (немесе жазықтықпен кеңiстiк қисығы үшiн) қиылысу нүктелерiнiң санын айтады.

8. Беттің нұсқасы (очеркі).

Беттің нұсқасы деп оның берілген проекциялар жазықтығына қарағанда көріну сызығының проекциясын айтады. Қайсыбір φ бетін π’ жазықтығына параллель проекциялау үшін осы φ бетін жанайтын берілген бағытқа параллель проекциялаушы сәулелер жүргізеді. Осы проекциялаушы сәулелердің φ бетімен жаанусы нүктелері A, B, C қайсыбір k сызығын анықтайды. Бұл k сызығын көріну сызығы деп атайды. k’ сызығы φ бетінің нұсқасы.

9. Конустық бет және оны эпюрде (сызбада) кескіндеу.

Конустық бет - белгілі бір сызықтың (S бағыттаушы) барлық нүктесін кеңістіктің берілген нүктесімен (m төбесімен) қосатын түзулердің (l’ жасаушыларының) геометриялық орны.

10 . Цилиндірлік бет, және оның эпюрдегі(сызбадағы) кескіні.

Цилиндрлік бет — берілген бағытқа параллель және бағыттауыш сызық арқылы өтетін кеңістіктің жасаушы түзулерінің жиыны;

11. Бұрмалану көрсеткіштері (коэффисиенттері) арасындағы байланыс; қиғашбұрышты аксонометрияның негізгі формуласы.

Бўрмалану көрсеткiшi деп аксонометриялық масштабтың натурал масштабқа қатынасын айтады. Абсцисса осi бағытындағы бұрмалану көрсеткiшiн u, ордината осi бағытындағы бұрмалану көрсеткiшiн v және аппликата осi бағытындағы бұрмалану көрсеткiшiн w әрiптерiмен белгiлелiк. Сонда .

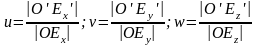Проекциялау бағытына қарай аксонометрияның тiк бұрышты және қиғаш бұрышты деп ажыратады. Тiк бұрышты аксонометрияда проекциялау бағыты проекциялар жазықтығына перпендикуляр (s') болады, ал қиғаш бұрышты аксонометрияда проекциялау бағыты проекциялар жазықтығына перпендикуляр болмайды (s').

Бұрмалану көрсеткiштерiне қарай аксонометрия үшке бөлiнедi: изометрия, диметрия және триметрия. Изометрияда: u=v=w. Диметрияда u=vw,. Триметрияда uvwu.

Қиғаш бұрышты акс-я нег формуласы: u²+v²+w²=2+ctg²..