29.1 Принцип гюйгенса-френеля

Расчет и объяснение дифракции света можно приближенно сделать, используя принцип Гюйгенса-Френеля.

Согласно Гюйгенсу, каждая точка волновой поверхности, которой достигла в данный момент волна, является центром элементарных вторичных волн, их внешняя огибающая будет волновой поверхностью в последующий момент времени (рис. 24.9; S₁ и S₂ - волновые поверхности соответственно в моменты t₁ и t₂; t₂> t₁).

Френель дополнил это положение Гюйгенса, введя представление о когерентности вторичных волн и их интерференции.

В таком обобщенном виде эти идеи получили название принципа Гюйгенса-Френеля.

Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса- Френеля, интерференцию вторичных волн, попавших в эту точку от волновой поверхности. Для волновой поверхности произвольной формы такой расчет достаточно сложен, но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности и непрозрачной преграды) вычисления сравнительно просты. Волновую поверхность при этом разбивают на отдельные участки (зоны Френеля), расположенные определенным образом, что упрощает математические операции.

29.2. Дифракция на щели

На узкую длинную щель, расположенную в плоской непрозрачной преграде MN, нормально падает плоскопараллельный пучок монохроматического света

Если бы не было дифракции, то световые лучи, пройдя через щель, сфокусировались бы в точке О, лежащей на главной оптической оси линзы. Дифракция света на щели существенно изменяет явление.

Будем считать, что все лучи пучка света исходят от одного удаленного источника¹ и, следовательно, когерентны. АВ есть часть волновой поверхности, каждая точка которой является центром вторичных волн, распространяющихся за щелью по всевозможным направлениям. Изобразить все эти вторичные волны невозможно.

Дифракция света, как и интерференция, связана с перераспределением энергии электромагнитных волн в пространстве. В этом смысле щель в непрозрачном экране является не просто системой, ограничивающей приложение светового потока, но перераспределителем этого потока в пространстве.

29.3. Дифракционная решетка - оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга щелей.

Дифракционную решетку можно получить нанесением непрозрачных царапин (штрихов) на стеклянную пластину. Непроцарапанные места - щели - будут пропускать свет; штрихи, соответствующие промежутку между щелями, рассеивают и не пропускают света.

Расстояние между центрами соседних щелей называют постоянной или периодом дифракционной решетки:

С= а+в

где а - ширина щели; b - ширина промежутка между щелями.

Если на решетку падает пучок когерентных волн, то вторичные волны, идущие по всем возможным направлениям, будут интерферировать, формируя дифракционную картину.

 Равенство

|A’ B’|=kλ ,или с*sin α=± kλ

является основной формулой дифракционной решетки

Между главными максимумами образуются минимумы (добавочные), число которых зависит от числа всех щелей решетки.

При падении на дифракционную решетку белого или иного немонохроматического света каждый главный максимум, кроме центрального, окажется разложенным в спектр [см. (24.29)]. В этом случае k указывает порядок спектра

Таким образом, решетка является спектральным прибором, поэтому для неё существенны характеристики, которые позволяют оценивать возможность различения спектральных линий.

Одна из таких характеристик-угловая дисперсия- определяет угловую ширину спектра. Она численно равна угловому расстоянию dα между двумя линиями спектра, длины волн которых различаются на единицу: D= dα/dλ

Возможность различать близкие спектральные линии зависит не только от ширины спектра, или угловой дисперсии, но и от ширины спектральных линий, которые могут накладываться друг на друга.

Разрешение спектральных линий количественно оценивается разрешающей способностью, равно отношению длины волны к наименьшему интервалу длин волн, которые еще могут быть разрешены: R=λ/ λ

29.4. Основная формула (24.29) дифракционной решетки может быть использована не только для определения длины волны, но и для решения обратной задачи - нахождения постоянной дифракционной решетки по известной длине волны. Такая скромная применительно к обычной дифракционной решетке задача подводит к практически важному вопросу - измерению параметров кристаллической решетки посредством дифракции рентгеновских лучей, что является содержанием рентгено-структурного анализа.

Пусть совмещены две дифракционные решетки, штрихи которых перпендикулярны. Для решеток выполняются условия главных максимумов: с₁*sin α₁ =± k₁λ , с₂ *sin α₂  =± k₂λ

Углы α₁ и α₂ отсчитываются во взаимно перпендикулярных направлениях. В этом случае на экране появится система пятен, каждому из которых соответствует пара значений k₁ и k₂ или α₁ и α₂. Таким образом, и здесь можно найти с₁ и с₂ по положению дифракционных пятен.

Усложняя задачу, логично считать, что дифракционная картина позволит измерить параметры и для трехмерной периодической структуры.

Естественной объемной периодической структурой являются кристаллы, крупные молекулы и т.п. Вторичные волны в кристалле возникают в результате взаимодействия первичных лучей с электронами атомов.

В настоящее время широко применяют рентгеноструктурный анализ биологических молекул и систем- рентгенограммы белков. Этим методом Дж. Уотсон и Ф. Крик установили структуру ДНК и были удостоены Нобелевской премии (1962). Использование дифракции рентгеновских лучей от кристаллов для исследования их спектрального состава относится к области рентгеновской спектроскопии.

29.5. Голография¹ - метод записи и восстановления изображения, основанный на интерференции и дифракции волн.

Идея голографии была впервые высказана Д. Габором в 1948 г., однако ее практическое использование оказалось возможно после появления лазеров.

¹ Голография (грен.) - метод полной записи.

Изложение голографии уместно начать сравнением с фотографией. При фотографировании на фотопленке фиксируется интенсивность световых волн, отраженных предметом. Изображение в этом случае является совокупностью темных и светлых точек. Фазы рассеиваемых волн не регистрируются, и, таким образом, пропадает значительная часть информации о предмете.

Голография позволяет фиксировать и воспроизводить более полные сведения об объекте с учетом амплитуд и фаз волн, рассеянных предметом. Регистрация фазы возможна вследствие интерференции волн. С этой целью на светофиксирующую поверхность посылают две когерентные волны: опорную, идущую непосредственно от источника света или зеркал, которые используют как вспомогательные устройства, и сигнальную, которая появляется при рассеянии (отражении) части опорной волны предметом и содержит соответствующую информацию о нем.

Интерференционную картину, образованную сложением сигнальной и опорной волн и зафиксированную на светочувствительной пластинке, называют голограммой. Для восстановления изображения голограмму освещают той же опорной волной.

30. Электромагнитную волну, в которой векторы е и, следовательно, векторы н лежат во вполне определенных плоскостях, называют пло-скополяризованной.

Плоскость, проходящая через электрический вектор е в направлении распространения электромагнитной волны, является плоскостью поляризации.

Плоскополяризованную волну излучает отдельный атом. В естественном свете, идущем от Солнца, накаленной нити лампы, газоразрядной трубки, пламени и т.п., складываются неупорядоченные излучения множества хаотически ориентированных атомов, поэтому направление е не выдерживается в одной плоскости¹. Такой свет можно рассматривать как наложение плоскополяризованных волн с хаотической ориентацией плоскостей колебаний, электрические векторы ориентированы по всевозможным перпендикулярным лучу направлениям. 

Устройство, позволяющее получать поляризованный свет из естественного, называют поляризатором. Он пропускает только составляющую вектора е на некоторую плоскость - главную плоскость поляризатора.

При этом через поляризатор проходит поляризованный свет¹, интенсивность которого равна половине интенсивности падающего света. При вращении поляризатора относительно луча естественного света поворачивается плоскость колебаний вышедшего плоскополяризованного света, но интенсивность его не изменяется. Поляризатор можно использовать для анализа поляризованного света, тогда его называютанализатором.

Если плоскополяризованный свет с амплитудой электрического вектора Е₀ падает на анализатор, то он пропустит только составляющую вектора е₀ , равную:

Е₌ Е_{0 cos}

где φ - угол между главными плоскостями поляризатора р и анализат ра А (рис. 25.3).

Так как интенсивность света пропорциональна квадрату амплитуд колебаний, получаем:

I=I_{0 cos}²

Где i₀ - интенсивность плоскополяризованного света, падающего на анализатор; i - интенсивность света, вышедшего из анализатора. Равенство выражает закон Малюса.

Как видно из закона Малюса, при повороте анализатора относительно луча падающего плоскополяризованного света интенсивность вышедшего света изменяется от нуля до I₀. Если при повороте анализатора относительно падающего луча как оси вращения интенсивность прошедшего света не изменяется, то свет может быть естественным¹; если при этом интенсивность изменяется по закону (25.2), то падающий свет - плоскополяризованный.

Термин «поляризация света» имеет два смысла. Во-первых, под этим понимают свойство света, характеризующееся пространственно-временной упорядоченностью ориентации электрического и магнитного векторов. Во-вторых, поляризацией света называют процесс получения поляризованного света.

30.1. При отражении от границы двух диэлектриков естественный свет частично поляризуется.

В отраженном луче преобладают колебания, перпендикулярные плоскости падения, а в преломленном - параллельные ей. Если угол падения удовлетворяет условию:

tg I_Б=n

то отраженный луч полностью плоскополяризован (рис. 25.5). Соотношение (25.3) выражает закон Брюстера.Здесь угол падения /_Б - угол Брюсте-ра, или угол полной поляризации; η - относительный показатель преломления двух сред.

Преломленный луч при выполнении закона Брюстера частично поляризован, при этом степень его поляризации наибольшая.

Используя (25.3) и закон преломления, нетрудно показать, что при полной поляризации отраженного света угол между преломленным и отраженным лучами равен 90°.

Таким образом, граница двух диэлектриков или диэлектрика и вакуума является поляризатором.

В качестве поляризатора используют также стопу стеклянных пластин. Независимо от угла падения и выполнения закона Брюстера степень поляризации преломленного луча возрастает по мере прохождения пластин.

30.2.  ПОЛЯРИЗАЦИЯ СВЕТА ПРИ ДВОЙНОМ ЛУЧЕПРЕЛОМЛЕНИИ

Некоторые прозрачные кристаллы обладают свойством двойного лучепреломления: при попадании света на кристалл луч раздваивается. Для одного из лучей выполняются законы преломления и поэтому этот луч называют обыкновенным, для другого - не выполняются и луч называют необыкновенным.

Направления, вдоль которых двойного лучепреломления нет и оба луча - обыкновенный и необыкновенный - распространяются с одной скоростью, называют оптическими осями кристалла (пунктир на рис. 25.7). Если такое направление одно, то кристаллы называют одноосными (они и рассматриваются в этом параграфе). К ним относят исландский шпат (разновидность углекислого кальция СаСО₃ - кристаллы гексагональной системы), кварц, турмалин (сложный алюмосиликат, кристаллы тригональной системы) и др. Плоскость, проходящая через оптическую ось и падающий луч, является главной. Колебания обыкновенного луча перпендикулярны главной плоскости, а необыкновенного лежат в главной плоскости, т.е. эти лучи поляризованы во взаимно перпендикулярных плоскостях.

Двойное лучепреломление обусловлено особенностями распространения электро магнитных волн в анизотропных средах: амплитуды вынужденных колебаний электронов зависят от направлений этих колебаний.

Ход обыкновенных и необыкновенных лучей в кристаллах можно наглядно представить с помощью волновых поверхностей.

30.3. ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ.

ПОЛЯРИМЕТРИЯ

Вращение плоскости поляризации, обнаруженное впервые на кристаллах кварца, заключается в повороте плоскости поляризации пло-скополяризованного света при прохождении через вещество. Вещества, обладающие таким свойством, называют оптически активными.

Пусть монохроматический свет падает от источника S на систему поляризатор Р-анализатор А (рис. 25.10), которые поставлены скрещенно, т.е. их главные плоскости взаимно перпендикулярны. В этом случае свет до наблюдателя не дойдет, так как анализатор не пропускает в соответствии с законом Малюса (φ = 90°) плоскополяризованный свет.

Если между поляризатором и анализатором поместить кварцевую пластинку так, чтобы свет проходил вдоль ее оптической оси, то в общем случае свет дойдет до наблюдателя. Если же анализатор повернуть на некоторый угол, то можно вновь добиться затемнения. Это свидетельствует о том, что кварцевая пластинка вызвала поворот плоскости поляризации на угол, соответствующий повороту анализатора для получения затемнения.

Используя в опыте свет различной длины волн, можно обнаружить дисперсию вращения плоскости поляризации (вращательную дисперсию), т.е. зависимость угла поворота от длины волны. Кварцевая пластинка толщиной 1 мм поворачивает плоскость поляризации приблизительно на следующие углы.

Для определенной длины волны угол α поворота плоскости поляризации пропорционален расстоянию /, пройденному светом в оптически активном веществе:

α = α0 /,

где α₀ - коэффициент пропорциональности, или постоянная вращения (вращательная способность), град/мм.

Существует две модификации кварца, каждая из которых поворачивает плоскость поляризации в определенном направлении: по часовой стрелке - правовращающий (положительный) кварц, против часовой

стрелки¹ - левовращающий (отрицательный). Постоянная вращения в обоих случаях одинакова.

Поляриметрию применяют не только для определения концентрации растворов, но и как метод исследования структурных превращений, в частности в молекулярной биофизике. В качестве примера на рис. 25.11 приведен график изменения удельного вращения [α₀] в одном из полипептидов в зависимости от состава растворителя, являющегося бинарной смесью хлороформа CHCl₃ и дихлоруксусной кислоты СНС1₂СООН. При 80% дихлоруксусной кислоты происходит резкое падение оптической активности, что свидетельствует об изменении кон-формации молекул полипептида.

30.4.  ИССЛЕДОВАНИЕ БИОЛОГИЧЕСКИХ ТКАНЕЙ В ПОЛЯРИЗОВАННОМ СВЕТЕ

Рассматривая прозрачные биологические объекты в микроскопе, трудно выявить различные структуры, поэтому приходится применять некоторые специальные методики; в их числе поляризационная микроскопия.

Поляризационный микроскоп аналогичен обычному биологическому микроскопу, но имеет поляризатор перед конденсором и анализатор в тубусе между объективом и окуляром. Предметный столик может вращаться вокруг оптической оси микроскопа. Таким образом, объект

освещают поляризованными лучами и рассматривают через анализатор.

Если скрестить поляризатор и анализатор, то поле зрения будет темным, таким же оно останется при помещении на предметный столик изотропных прозрачных тел. Анизотропные предметы изменяют поле зрения в соответствии с тем влиянием, которое они окажут на направление плоскости колебаний поляризованного света.

Так как некоторые ткани (мышечная, костная, нервная) обладают оптической анизотропией, возможна поляризационная микроскопия биологических объектов. При скрещенных поляризаторе и анализаторе будут видны только те волокна, анизотропия которых изменяет поляризованный свет.

Поляризованный свет можно использовать в модельных условиях для оценки механических напряжений, возникающих в костных тканях. Этот метод основан на явлении фотоупругости, которое заключается в возникновении оптической анизотропии в первоначально изотропных твердых телах под действием механических нагрузок.

Из прозрачного изотропного материала, например плексигласа, создают плоскую модель кости. В скрещенных поляроидах эта модель незаметна, так как выглядит темной. Прикладывая нагрузку, вызывают анизотропию плексигласа, что становится заметным по характерной картине полос и пятен (рис. 25.12). По этой картине, а также по ее изменению при увеличении или уменьшении нагрузки можно делать выводы о механических напряжениях, возникающих в модели, а следовательно, и в натуре.

21. Электрическое поле есть разновидность материи, посредством которой осуществляется силовое воздействие на электрические заряды, находящиеся в этом поле. Характеристики электрическою поля, которое генерируется биологическими структурами, являются источником информации о состоянии организма.

21.1.Силовой характеристикой электрического поля является напряженность, равная отношению силы, действующей в данной точке поля на точечный заряд, к этому заряду:

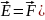
Напряженность - вектор, направление которого совпадает с направлением силы, действующей в данной точке поля на положительный точечный заряд.

Напряженность эл.поля в произвольных точках аналитически задается следующими тремя уравнениями:

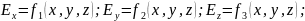
Эл.поле графически удобно представлять силовыми линиями, касательные к которым совпадают с направлением вектора напряженности в соответствующих точках поля.

Работа сил электростатического поля не зависит от траектории, по которой перемещается заряд в этом поле. Поля, обладающие таким свойством, называют потенциальными. Работа сил электростатического поля по перемещению заряда по замкнутой траектории равна нулю

Разностью потенциалов между точками поля называют отношение работы, совершаемой силами поля при перемещении точечного положительного заряда из одной точки поля в другую, к этому заряду:

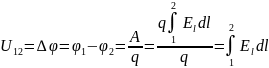
Наряду с разностью потенциалов в качестве характеристики эл.поля используют понятие потенциала. Однако для данной точки поля оно имеет однозначный смысл только в том случае, если задан потенциал какой-либо произвольной точки поля.

Потенциалы эл.поля в различных точках наглядно можно представить в виде поверхностей одинакогвого потенциала.Обычно проводят эквипотенциальные поверхности, отличающиеся от соседних на одно и то же значение потенциала.

21.2. Так как напряженность эл.поля определяется через силу, а потенциал- через работу сил поля, то эти характеристики связаны между собой анологично силе и работе. Интегральная зависимость напряженности поля и потенциала дается формулой или выражением

Силовые линии и эквипотенциальные поверхности взаимно перпендикулярны.

21.3. ЭЛЕКТРИЧЕСКИЙ ДИПОЛЬ

Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя). Основной характеристикой диполя является его электрический, или дипольный момент - вектор, равный произведению заряда на плечо диполя, направленный от отрицательного заряда к положительному:

Единицей эл.момента диполя является кулон-метр.

На диполь в однородном эл.поле действует момент силы, зависящий от эл.момента и ориентации диполя, а также напряженности поля.

На диполь действует сила, зависящая от его эл.момента и степени неоднородности поля dE/dx. Если диполь ориентирован в неоднородном эл.поле не вдоль силовой линии, то на него дополнительно действует еще и момент силы. Таким образом, свободный диполь ориентируется вдоль силовых линий и втягивается в область больших значений напряженности поля.

21.4. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ

Диэлектриками называют тела, не проводящие электрического тока.

Термин «диэлектрик» введен М. Фарадеем для обозначения веществ, через которые проникают электрические поля, в отличие от металлов, внутри которых электростатического поля нет. К диэлектрикам относят твердые тела, такие, как эбонит, фарфор, жидкости (например, чистая вода), газы.

При изменении внешних условий (нагревание, радиоактивное облучение и т.п.) диэлектрик может проводить электрический ток. Изменение состояния диэлектрика при помещении в электрическое поле можно объяснить его молекулярным строением. Условно выделим три класса диэлектриков:

1) с полярными молекулами;

2) с неполярными молекулами;

3) кристаллические.

К первому классу принадлежат такие вещества, как вода, нитробензол и др. Молекулы этих диэлектриков не симметричны, центры масс их положительных и отрицательных зарядов не совпадают, и они обладают электрическим моментом диполя даже в случае, когда электрического поля нет.

Ко второму классу диэлектриков относят такие вещества(например, водород,кислород и др.), молекулы которых в отсутствие эл.поля не имеют дипольных моментов. Втаких молекулах заряды электронов и ядер расположены так, что «центры масс» положительных и отрицательных зарядов совпадают. Если неполярную молекулу поместить в эл.поле, то разноименные заряды несколько сместяться в противоположные стороны и молекула будет иметь дипольный момент.

Третий класс- кристаллические диэлектрики, решетка которые состоит из положительных и отрицательных ионов. Такой диэлектрик можно схематически рассматривать как совокупность двух «подрешеток», одна из которых заряжена положительно, другая- отрицательно. При отсутствии поля подрешетки расположены симметрично и суммарный электрический момент такого диэлектрика равен нулю. Если диэлектрик поместить в эл.поле, то подрешетки немного сместяться в противоположные стороны и диэлектрик приобретает электрический момент.

Все эти процессы, происходящие в разных диэлектриках при наложении эл.поля, объединяют общим термином поляризация,т.е. приобретение диэлектриком дипольного момента.

Для первого классадиэлектриков характерна ориентационная поляризация, для второго-электронная, т.е. смещение главным образом электронных оболочек, для третьего- ионная.

Для оценки состояния поляризации диэлектрика вводят велечину, называемую поляризованностью, среднее значение которо равно отношению суммарного эл.момента элемента объема V диэлектрика к этому объему:

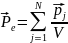
Единицей поляризованности является кулон на квадратный метр (Кл/м²).

При поляризации диэлектрика на одной его поверхности (грани) создаются положительные заряды, а на другой - отрицательные Эти электрические заряды называют связанными, так как они принадлежат молекулам диэлектрика (или кристаллической решетке при ионной поляризации) и не могут перемещаться в отрыве от молекул или быть удалены с поверхности диэлектрика в отличие от свободных зарядов, которых в идеальном диэлектрике нет.

При возрастании напряженности электрического поля упорядочивается ориентация молекул (ориентационная поляризация), увеличиваются дипольные моменты молекул (электронная поляризация), а также происходит смещение подрешеток (ионная поляризация) - все это приводит к увеличению поверхностной плотности а_св связанных электрических зарядов.

21.5. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ

Система зарядов или заряженных тел, заряженный конденсатор обладают энергией.

В этом можно убедиться, разряжая, например, конденсатор через лампочку, присоединенную к нему: лампочка вспыхнет.

Вычислим энергию поля конденсатора. Чтобы зарядить его, будем многократно переносить положительный заряд dq с одной обкладки на другую. По мере его переноса увеличивается напряжение между обкладками конденсатора. Работа, которую необходимо совершить против сил электрического поля для зарядки конденсатора, равна энергии конденсатора:

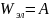
Энергия поля заряженного конденсатора:

Предполагая, что эл.поле плоского конденсатора однородно, разделим на объем и получим объемную плотность энергии поля:

Единицей объемной плотности является джоуль на кубический метр (Дж/м3).