4.2. Решение задачи 2

Рассмотрим пример построения линии пересечения конуса и сферы способом секущих плоскостей.

Задано: конус (высота H=100 мм, радиус основания R=45 мм), и сфера (радиус r =35 мм). Центр сферы смещен вверх на расстояние a=40 мм от основания конуса и вправо на расстояние b=25 мм от оси вращения.

Последовательность построения линии пересечения конуса и сферы такова:

1. Строим две проекции конуса и сферы по исходным данным (рис. 4а).

2. Отмечаем на фронтальной проекции опорные точки A₂ и B₂ – точки пересечения очерковых линий конуса со сферой и находим горизонтальные проекции A₁ и B₁ точек А и В (рис. к 4б). Проекции линии пересечения двух поверхностей находятся между точками A₂ и B₂, т.е. в зоне наложения проекций конуса и сферы.

3. Строим промежуточную точку D линии пересечения (рисунок 4в). Для этого:

– строим фронтальную проекцию ₂ вспомогательной секущей плоскости . Эта плоскость пересекает коническую поверхность по окружности m₂ радиусом R_К, а сферу – по окружности n₂ радиусом R_С;

– строим горизонтальные m₁ и n₁ проекции окружностей m и n и определяем точки D₁ и D₁ пересечения этих окружностей;

– строим фронтальные проекции точек D₂ и D₂ точки D. Для этого проводим из точек D₁ и D₁ линии связи до пересечения с фронтальной проекцией m₂ и n₂ окружностей m и n в точках D₂ и D₂.

На чертеже точки обозначенные буквами со штрихом не обозначены.

4. Повторяем предыдущую операцию необходимое число раз и определяем проекции промежуточных точек C, E, F, G.

5. Соединяем полученные точки линией с учетом её видимости в проекциях (рис. 4г). Обводим штриховой линией невидимую часть очерковой линии сферы и конуса на фронтальной проекции между точками А₂ и В₂ и горизонтальную проекцию очерковой линии сферы и конуса между точками А₁ и В₁.

Точка экстремума на фронтальной проекции линии пересечения определяется с помощью способа сфер (точка D₂ на рис. 5.5в).

Рассмотрим пример построения линии пересечения конуса и сферы способом секущих сфер.

1. Строим две проекции конуса и сферы по заданным ранее параметрам (рис. 5а) и определяем фронтальную проекцию О₂ центра О секущих сфер-посредников.

2. Определяем фронтальные проекции опорных точек A₂ и B₂ – точек пересечения очерковых линий конуса со сферой и строим горизонтальные проекции этих точек – A₁ и B₁ (рис. 5б).

Помним, что линия пересечения поверхностей должна находиться в зоне наложения проекций конуса и сферы.

3. Определяем минимальный и максимальный радиусы сфер-посредников (рис. 5б). Для определения минимального радиуса R_min сфер необходимо из центра сфер провести перпендикуляр О₂К₂ к образующей конуса О₂К₂ = R_min. Максимальный радиус R_max сферы равен расстоянию от центра О₂ до наиболее удаленной точки В₂ пересечения очерков поверхностей, т.е. R_max= О₂В₂.

4. Строим промежуточные точки линии пересечения конуса и сферы (рис. 5в).

4.1. Строим фронтальную проекцию Г₂ вспомогательной сферы Г минимального радиуса.

Рис. 4

Для чего: – из центра O2 сфер строим фронтальную проекцию Г2 вспомогательной сферы Г, радиусом Rmin = O2K2, которая касается конической поверхности по окружности m, а заданную сферу пересекает по окружности n; 4.2. Строим точки D2 и (D2') пересечения окружностей m2 и n2. 4.3. Определяем горизонтальные проекции D1 и (D1') точек пересечения D и (D') окружностей. 4.4. Строим еще несколько вспомогательных сфер-посредников Г1…Г4, которые могут пересекать конус по двум окружностям, а сферу по одной окружности. 4.5. Строим проекции промежуточных точек линии пересечения поверхностей. 4.6. Соединяем полученные точки сплошной толстой линией с учетом её видимости в проекциях (рис. 5г). Рис. 5 4.3. решение задачи 3 Рассмотрим пример построения развертки усеченной пирамиды (рис. 6) способом триангуляции. Развертка пирамиды состоит из боковой поверхности S123456, состоящей из шести треугольников S12,…S61, основания – правильного шестиугольника 123456 и плоскостей, полученных при сечении пирамиды секущими плоскостями. При построении развертки пирамиды будем придерживаться следующей последовательности: 1. Строим полную развертку боковой поверхности пирамиды по ребру S4 = b и стороне основания шестиугольника 34 = d измеренными на рис. 6. Рис. 6 2. Переносим на развертку опорные точки ABCDEFG1 выреза, как точки, лежащие на ребрах пирамиды. Расстояние от вершины до соответствующей точки определяется на ребре S1 (рис. 6). Например, истинное расстояние от вершины S до точки D равно S2D0 (рис. 6). Откладываем отрезок S2D0 на образующей S0D0, построенной на развертке (рис. 7). Точки С и Е, лежащие на линии пересечения граней пирамиды с плоскостью Г, строим на развертке следующим образом: – проводим через фронтальные проекции С2 и Е2 точек С и Е проекции S2K2 и S2M2 линии посредники SK и SM (рис. 6); – достраиваем горизонтальные проекции S1K1 и S1M1 линий посредников SK и SM; – строим линии посредники S0K0 и S0M0. Для этого откладываем на развертке отрезки 21К1 и 31М1 от точек 20 и 30 соответственно (рис. 7); – проводим из точки D0 прямые линии параллельные линиям 2030 и 3040 до пересечения с линиями S0K0 и S0M0 в точках Е0 и С0. 3. Определяем развертки фигур, полученных в результате сечения пирамиды плоскостями. Натуральная величина фигуры ABCC1B1A, полученной от сечения профильной плоскостью  равна замкнутому контуру A3B3C3C3'B3'A3. Симметричные точки со штрихами на рис. 6 не обозначены. Натуральная величина фигуры CDEE'D'C', полученной от сечения горизонтальной плоскостью Г равна замкнутому контуру C1D1E1E1'D1'C1' (рис. 6). Рис. 7

Натуральная величина фигуры 1GFEE'F'G' сечения фронтально проецирующей плоскостью Т равна контуру 1₂G₂F₂E₂E₂'F₂'G₂', полученной способом замены плоскостей проекций (рис. 8).

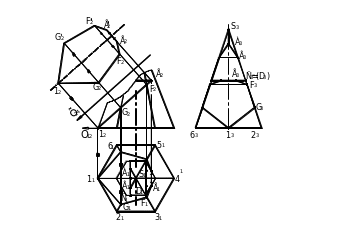
Рис. 8

4. Строим развертку основания пирамиды и развертку фигур, полученных от сечения плоскостями , ГиТ (рис. 9).

Рис. 9

Полная развертка пирамиды приведена на рис. 1.