1 Рациональное поведение потребителя
1.1 Бюджетная линия
Задача 1
Пенсионер имеет доход R руб. в месяц и весь он должен быть израсходован на покупку двух товаров А и Б. Товар А стоит P1 руб., а товар Б — P2 руб. Нарисуйте бюджетную линию. Какой будет бюджетная линия, если доход пенсионера вырастает до R1 руб.? Какой будет бюджетная линия при доходе R руб., но снижении цены товара А до P3 руб.
Вариант |
1 |
2 |
3 |
4 |
5 |
R |
1000 |
3000 |
500 |
4000 |
5000 |
P1 |
25 |
75 |
12,5 |
100 |
125 |
P2 |
50 |
150 |
25 |
200 |
250 |
R1 |
1200 |
3600 |
600 |
4800 |
6000 |
P3 |
20 |
60 |
10 |
80 |
100 |
Задача 2
Цена тюльпанов = P1 руб, орхидей – P2 руб. Доход
потребителя - R руб. Набор безразличия двух товаров задан в таблице :
Тюльпан |
Х1 |
Х2 |
Х3 |
Х4 |
Орхидея |
Y1 |
Y2 |
Y3 |
Y4 |
Построить бюджетную линию и кривую безразличия. Определить точку
равновесия потребителя, наклон бюджетной линии, предельную норму
замещения.
Вариант |
1 |
2 |
3 |
4 |
5 |
R |
28 |
14 |
84 |
7 |
35 |
P1 |
1 |
0,5 |
3 |
0,25 |
1,25 |
P2 |
2 |
1 |
6 |
0,5 |
2,5 |
X1 |
16 |
8 |
48 |
4 |
20 |
X2 |
12 |
6 |
36 |
3 |
15 |
X3 |
8 |
4 |
24 |
2 |
10 |
X4 |
4 |
2 |
12 |
1 |
5 |
Y1 |
6 |
3 |
18 |
1,5 |
7,5 |
Y2 |
8 |
4 |
24 |
2 |
10 |
Y3 |
12 |
6 |
36 |
3 |
15 |
Y4 |
24 |
12 |
72 |
6 |
30 |
Задача 3
Задана следующая зависимость изменения совокупной полезности в зависимости от изменения объема потребления:
Q |
Tuг |
Tuс |
1 |
Х1 |
У1 |
2 |
Х2 |
У2 |
3 |
Х3 |
У3 |
4 |
Х4 |
У4 |
5 |
Х5 |
У5 |
Известно также, что цена говядины составляет Ргд.ед., а свинины -Рсд.ед., бюджет потребителя равен I д.ед.
Рассчитайте какое количество двух сортов мяса приобретет рациональный потребитель, на основе полученных результатов постройте график потребительского выбора (кривую безразличия построить произвольно, указав лишь объем совокупной полезности, который ей соответствует).
Вариант |
1 |
2 |
3 |
4 |
5 |
x1 |
18 |
27 |
9 |
36 |
58,5 |
x2 |
34 |
51 |
17 |
68 |
110,5 |
x3 |
48 |
72 |
24 |
96 |
156 |
x4 |
60 |
90 |
30 |
120 |
195 |
x5 |
70 |
105 |
35 |
140 |
227,5 |
y1 |
12,5 |
18,75 |
6,25 |
25 |
40,625 |
y2 |
22,5 |
33,75 |
11,25 |
45 |
73,125 |
y3 |
30 |
45 |
15 |
60 |
97,5 |
y4 |
35 |
52,5 |
17,5 |
70 |
113,75 |
y5 |
37,5 |
56,25 |
18,75 |
75 |
121,875 |
Pa |
4 |
6 |
2 |
8 |
13 |
Pb |
2,5 |
3,75 |
1,25 |
5 |
8,125 |
I |
23,5 |
35,25 |
11,75 |
47 |
76,375 |
Задача 4
На рисунке показана кривая безразличия потребителя и его бюджетная линия. Напишите уравнение бюджетной линии, если цена товара Y равна Ру рублей.
Y
Х1
ХВариант |
1 |
2 |
3 |
4 |
5 |
Py |
6 |
13,5 |
10,5 |
18 |
21 |
Y1 |
10 |
22,5 |
17,5 |
30 |
35 |
X1 |
15 |
33,75 |
26,25 |
45 |
52,5 |
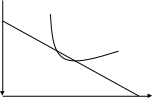
Задача 5
При первоначальном доходе I1 цена книг была равна Pк руб. Затем доход увеличился доI2 , а цена товара журналов увеличилась в n раза.
Определите по графику:
1) цену журналов до изменения дохода и после его увеличения ;
2) величину дохода до и после изменения ;
3) цену книг после увеличения дохода.
Вариант |
1 |
2 |
3 |
4 |
5 |
Pк |
50 |
12,5 |
125 |
5 |
6,25 |
n |
2 |
0,5 |
5 |
0,2 |
0,25 |
Q1 |
4 |
1 |
10 |
0,4 |
0,5 |
Q2 |
20 |
5 |
50 |
2 |
2,5 |
Q3 |
50 |
12,5 |
125 |
5 |
6,25 |
1.2 Максимизация полезности
Задача 6
Девочка получает на карманные расходы 6 руб. в неделю на карманные расходы. Эти деньги она тратит на покупку комиксов и наклеек. Каждая книга комиксов стоит 2 руб., а каждая наклейка – 1 руб. Полезность для нее каждую неделю складывается из полезности от комиксов и полезности от наклеек. Две составляющие функции полезности представлены в таблице. Какой потребительский набор выберет девочка?
Комиксы |
Конфеты |
||
Q |
TU |
Q |
TU |
0 |
X1 |
0 |
Y1 |
1 |
X2 |
1 |
Y2 |
2 |
X3 |
2 |
Y3 |
3 |
X4 |
3 |
Y4 |
4 |
X5 |
4 |
Y5 |
5 |
X6 |
5 |
Y6 |
Вариант |
1 |
2 |
3 |
4 |
5 |
X1 |
0 |
0 |
0 |
0 |
0 |
X2 |
12 |
15 |
18 |
10 |
16 |
X3 |
22 |
25 |
28 |
20 |
26 |
X4 |
30 |
33 |
36 |
28 |
34 |
X5 |
36 |
39 |
42 |
34 |
40 |
X6 |
41 |
44 |
47 |
39 |
45 |
Y1 |
0 |
0 |
0 |
0 |
0 |
Y2 |
8 |
11 |
14 |
6 |
12 |
Y3 |
13 |
16 |
19 |
11 |
17 |
Y4 |
17 |
20 |
23 |
15 |
21 |
Y5 |
20 |
23 |
26 |
18 |
24 |
Y6 |
22 |
25 |
28 |
20 |
26 |
Задача 7
Студент, готовясь к сдаче экзаменационной сессии, решил улучшить свою успеваемость по трём предметам: микроэкономике, математике и информатике. Для этого он решил воспользоваться платными услугами преподавателей. Стоимость индивидуальных занятий по всем предметам одинаковая и равна Ррублям за один час. Количество часов, которое студент имеет возможность заниматься в день – 9. Субъективные оценки предельной полезности каждого дополнительного часа занятий приведены в таблице.
Кол-во часов |
Микроэкономика |
Математика |
Информатика |
1 |
х1 |
у1 |
z1 |
2 |
х2 |
у2 |
z2 |
3 |
х3 |
у3 |
z3 |
4 |
х4 |
у4 |
z4 |
5 |
х5 |
у5 |
z5 |
Определите, как студент распределит свое время.
Вариант |
1 |
2 |
3 |
4 |
5 |
Р |
400 |
100 |
160 |
20 |
320 |
x1 |
10 |
2,5 |
4 |
0,5 |
8 |
x2 |
8 |
2 |
3,2 |
0,4 |
6,4 |
x3 |
6 |
1,5 |
2,4 |
0,3 |
4,8 |
x4 |
4 |
1 |
1,6 |
0,2 |
3,2 |
x5 |
2 |
0,5 |
0,8 |
0,1 |
1,6 |
y1 |
9 |
2,25 |
3,6 |
0,45 |
7,2 |
y2 |
5 |
1,25 |
2 |
0,25 |
4 |
y3 |
4 |
1 |
1,6 |
0,2 |
3,2 |
y4 |
2 |
0,5 |
0,8 |
0,1 |
1,6 |
y5 |
0 |
0 |
0 |
0 |
0 |
z1 |
7 |
1,75 |
2,8 |
0,35 |
5,6 |
z2 |
4 |
1 |
1,6 |
0,2 |
3,2 |
z3 |
2 |
0,5 |
0,8 |
0,1 |
1,6 |
z4 |
0 |
0 |
0 |
0 |
0 |
z5 |
-1 |
-0,25 |
-0,4 |
-0,05 |
-0,8 |
Задача 8
Таня решила израсходовать I рублей на покупку тортов. Полезность оценивается деньгами (сколько она готова заплатить за определённое количество или определённую единицу пирожного). Таня предполагает 2 варианта использования тортов: разделить их с одноклассниками или попить чай в кругу семьи. Вот как выглядит таблица её предпочтений:
Кол-во тортов |
Одноклассникам |
Семье |
1 |
х1 |
у1 |
2 |
х2 |
у2 |
3 |
х3 |
у3 |
4 |
х4 |
у4 |
5 |
х5 |
у5 |
Определите наилучший способ использования Таней этих денег, если цена одного торта – P рублей.
Вариант |
1 |
2 |
3 |
4 |
5 |
Р |
60 |
180 |
24 |
6 |
48 |
x1 |
8 |
24 |
3,2 |
0,8 |
6,4 |
x2 |
14 |
42 |
5,6 |
1,4 |
11,2 |
x3 |
19 |
57 |
7,6 |
1,9 |
15,2 |
x4 |
23 |
69 |
9,2 |
2,3 |
18,4 |
x5 |
26 |
78 |
10,4 |
2,6 |
20,8 |
y1 |
12 |
36 |
4,8 |
1,2 |
9,6 |
y2 |
21 |
63 |
8,4 |
2,1 |
16,8 |
y3 |
27 |
81 |
10,8 |
2,7 |
21,6 |
y4 |
30 |
90 |
12 |
3 |
24 |
y5 |
31 |
93 |
12,4 |
3,1 |
24,8 |
P |
8 |
24 |
3,2 |
0,8 |
6,4 |
Задача 9
В таблице указаны предельные полезности от приобретения каждой единицы четырехвидов блага: похода в ночной клуб, покупки книги, просмотра фильма в кинотеатре и покупкикомпакт-диска. Найти оптимальный набор для потребителя, выделяющего на эти четыре благаI руб., если цена похода в клуб составляет Р1руб, книги – Р2 руб., билета в кино – Р3 руб., а диска Р4 руб. Подсчитать полезность этого набора.
Q |
Клуб |
Книга |
Кино |
Диск |
1 |
х1 |
у1 |
z1 |
a1 |
2 |
х2 |
у2 |
z2 |
a2 |
3 |
х3 |
у3 |
z3 |
a3 |
4 |
х4 |
у4 |
z4 |
a4 |
5 |
х5 |
у5 |
z5 |
a5 |
Вариант |
1 |
2 |
3 |
4 |
5 |
I |
1000 |
50 |
400 |
100 |
800 |
P1 |
300 |
15 |
120 |
30 |
240 |
P2 |
150 |
7,5 |
60 |
15 |
120 |
P3 |
100 |
5 |
40 |
10 |
80 |
P4 |
75 |
3,75 |
30 |
7,5 |
60 |
x1 |
210 |
10,5 |
84 |
21 |
168 |
x2 |
180 |
9 |
72 |
18 |
144 |
x3 |
90 |
4,5 |
36 |
9 |
72 |
x4 |
75 |
3,75 |
30 |
7,5 |
60 |
x5 |
60 |
3 |
24 |
6 |
48 |
y1 |
180 |
9 |
72 |
18 |
144 |
y2 |
150 |
7,5 |
60 |
15 |
120 |
y3 |
120 |
6 |
48 |
12 |
96 |
y4 |
105 |
5,25 |
42 |
10,5 |
84 |
y5 |
90 |
4,5 |
36 |
9 |
72 |
z1 |
150 |
7,5 |
60 |
15 |
120 |
z2 |
100 |
5 |
40 |
10 |
80 |
z3 |
90 |
4,5 |
36 |
9 |
72 |
z4 |
80 |
4 |
32 |
8 |
64 |
z5 |
70 |
3,5 |
28 |
7 |
56 |
a1 |
90 |
4,5 |
36 |
9 |
72 |
a2 |
60 |
3 |
24 |
6 |
48 |
a3 |
60 |
3 |
24 |
6 |
48 |
a4 |
45 |
2,25 |
18 |
4,5 |
36 |
a5 |
45 |
2,25 |
18 |
4,5 |
36 |
Задача 10
Некий гражданин расходует свой бюджет (на 1 день) в размере I долл. на 2 товара: Х и Y. Полезность товаров X и Y при увеличении количества потребления представлена в таблице; цена товара “X” -PX долл.; товара “Y” -PY долл. Какое количество товара X и Y должен покупать потребитель, чтобы максимизировать полезность и находиться в потребительском равновесии?
Количество товара (Q) |
Общая полезность товара X, (TUX) |
Общая полезность товара Y, (TUY) |
1 |
X1 |
Y1 |
2 |
X2 |
Y2 |
3 |
X3 |
Y3 |
4 |
X4 |
Y4 |
5 |
X5 |
Y5 |
6 |
X6 |
Y6 |
7 |
X7 |
Y7 |
Вариант |
1 |
2 |
3 |
4 |
5 |
I |
10 |
0,5 |
4 |
1 |
8 |
Pх |
1 |
0,05 |
0,4 |
0,1 |
0,8 |
Py |
2 |
0,1 |
0,8 |
0,2 |
1,6 |
x1 |
10 |
0,5 |
4 |
1 |
8 |
x2 |
18 |
0,9 |
7,2 |
1,8 |
14,4 |
x3 |
25 |
1,25 |
10 |
2,5 |
20 |
x4 |
31 |
1,55 |
12,4 |
3,1 |
24,8 |
x5 |
36 |
1,8 |
14,4 |
3,6 |
28,8 |
x6 |
40 |
2 |
16 |
4 |
32 |
x7 |
43 |
2,15 |
17,2 |
4,3 |
34,4 |
y1 |
24 |
1,2 |
9,6 |
2,4 |
19,2 |
y2 |
44 |
2,2 |
17,6 |
4,4 |
35,2 |
y3 |
62 |
3,1 |
24,8 |
6,2 |
49,6 |
y4 |
78 |
3,9 |
31,2 |
7,8 |
62,4 |
y5 |
90 |
4,5 |
36 |
9 |
72 |
y6 |
96 |
4,8 |
38,4 |
9,6 |
76,8 |
y7 |
100 |
5 |
40 |
10 |
80 |