Тема 7. Управление очередями). [4, с.7-27, с.35-48].

Существование очередей - нормальное состояние производственной системы. Основа решения задачи управления очередью - компромисс между стоимостью ожидания и стоимостью мер по ускорению процесса обслуживания. Основные понятия математической теории систем массового обслуживания. Постановки и решения трёх задач, использующих разные типы моделей очередей.

Очереди существуют и на производстве (детали ждут своей очереди для обработки на станке, станки ждут очереди на капитальный ремонт) и в сфере услуг (очередь к кассе магазина, на заправку на автозаправочной станции, к парикмахеру). Существование очередей – это нормальное состояние производственной системы. Ими достаточно эффективно управляют с помощью средств системного менеджмента и проектирования.

Решение задачи управления очередью носит компромиссный характер между стоимостью ожидания в очереди и стоимостью мер по ускорению процесса обслуживания. Рассмотрим ситуацию внутри фирмы – служащие теряют рабочее время, ожидая в очереди либо к оборудованию, либо к другому сотруднику. Можно оценить эти потери в денежной стоимости и сравнить с затратами на установку дополнительного оборудования или привлечения к работе дополнительного сотрудника. Если потери большие, то следует пойти на дополнительные затраты.

К сожалению, возникают очереди, когда потери или потребности клиентов невозможно оценить в деньгах – например очередь пациентов для лечения в условиях стационара – больницы.

Для решения задач управления очередями применяется математическая теория систем массового обслуживания (СМО). Вначале рассмотрим основные понятия этой теории:

1. СМО состоит из 3-х компонентов: исходной генеральный совокупности клиентов сервисной системы, стоящих в очереди, самой сервисной системы, сценариев выхода клиентов из сервисной системы (покинуть навсегда или возвратиться в исходную генеральную совокупность).

2. Генеральная совокупность клиентов может быть конечной (финитной) – когда число клиентов ограничено и временно некоторые уходят из очереди (при этом вероятность появления следующей заявки снижается), затем возвращаются (вероятность следующей заявки возрастает). А может быть бесконечной (инфинитной) – когда число клиентов столь велико, что уход их из очереди и возвращение практически не влияет на вероятность появления заявки на обслуживание.

3. Интенсивность входящего потока λ - среднее число заявок за определенный период времени. Может быть постоянным при ритмичных процессах или переменным, что чаще и встречается.

4. Плотность распределения вероятности появления следующей заявки в момент t, после поступления предыдущей заявки в момент t=0, подчиняется экспоненциальному закону: среднее значение равно , а дисперсия . Тогда вероятность появления следующей заявки через t^’ или более единицы времени (например, минут) после предыдущей на рисунке это значение площади под кривой, заштрихованный так ///. Вероятность появления следующей заявки в течение t^’ единицы времени после предыдущей на рисунке подсчитывается как площадь фигуры, заштрихованный ≡, или по формуле .

f (t)

f (t) = λ e ^{–λ t}

t

t¹

2. Для расчета вероятности поступления заданного числа n произвольно входящих заявок за определенный период времени Т используется закон распределения вероятностей Пуассона:

P_T (n)= (λ t) ⁿ e ^{–λ t}

n !

графически он имеет вид.

P_T (n)

n (число поступающих заявок)

Среднее значение и дисперсия распределения Пуассона одинаковы и равны λ.

6. Спрос на услуги может быть управляемым (сезонные распродажи в магазинах, конкретные часы работы предприятия) и неуправляемым (потребность в скорой медицинской помощи).

7. Единичная (одиночная) заявка – наименьшее число для измерения входящего потока (1 посетитель ресторана, пакет из 100 акций на фондовой бирже). Групповые заявки состоят из некоторого количества единичных заявок (компания из 5 человек, заказавшая столик в ресторане).

8. Клиенты (заявки) могут быть разные по уровню терпеливости:

Терпеливые – ждут момента оказания услуги до конца, пока их не обслужат.

Нетерпеливые – неприсоединившиеся к очереди после ее осмотра.

Нетерпеливые - с переоценкой условий ожидания (постояв в очереди, все же уходят).

9. Основные характеристики очередей: длина очереди, количество очередей, дисциплина очереди. Длина очереди бывает обусловлена ограниченной пропускной способностью сервисной системы; причем в случаях, когда она очень низка и очередь становится очень длинной, такую очередь называют бесконечной.

Очереди бывают однолинейные и многолинейные, состоящие из нескольких однолинейных, образующихся к нескольким каналам обслуживания и даже к одному путем соединения в одну линию.

Дисциплина очереди – это правило, по которому устанавливается порядок обслуживания клиентов. От правил назначения приоритета обслуживания зависит количество клиентов в очереди, среднее время ожидания, диапазон варьирования длины очереди, продуктивность работы сервисной системы и другие. Примеры правил:

- первоочередное обслуживание в хронологическом порядке прибытия

- первоочередное обслуживание по предварительным заказам

- первоочередное обслуживание в случаях крайней необходимости

- первоочередное обслуживание наиболее доходных клиентов

- первоочередное обслуживание самых больших заказов

- первоочередное обслуживание постоянных клиентов

- первоочередное обслуживание по ближайшей обещанной дате

- первоочередное обслуживание клиентов с наименьшим временем обслуживания

Можно применить одновременно несколько приоритетов для образования дисциплины очереди, построив их в порядке значимости.

10. Интенсивность обслуживания μ – среднее число клиентов, обслуженных за определенный период времени.

11. Время обслуживания может быть постоянным или произвольным. В последнем случае для описания плотности распределения вероятности времени обслуживания используют закон .

12. В зависимости от количества клиентов и ограничений на порядок обслуживания, выбирается структура очереди. Она может быть:

- одноканальной однофазовой;

- одноканальной многофазовой, то есть состоящий из последовательности операций;

- многоканальной однофазовой;

- многоканальной многофазовой;

- комбинированной – с переходом многоканального обслуживания в одноканальное;

- комбинированной - альтернативного пути (либо это вариант многофазовой многоканальной структуры с возможностью перехода клиентов из одного канала в другой после завершения первой обслуживающей операции либо варьируется количество фаз и каналов также после первой обслуживающей операции).

Далее рассмотрим примеры решения конкретных задач для 3-х типов моделей очередей [ ]. Во всех моделях используются следующие предположения:

- одна фаза обслуживания;

- распределение потока пуассоновское;

- дисциплина очереди - в порядке поступления;

- неограниченная длина входной очереди;

- структура одноканальная (в 3 модели многоканальная);

- исходящая генеральная совокупность бесконечная;

- распределение операций обслуживания экспоненциальное (во 2 модели равномерное).

Используем обозначения:

среднее время обслуживания;

среднее время между заявками;

для 1 канала обслуживания это коэффициент загрузки;

среднее число заявок, ожидающих в очереди;

среднее число заявок в системе, включая обслуживаемых;

среднее время ожидания в очереди

среднее время пребывания в системе, включая время обслуживания;

n – количество заявок в системе;

М – количество идентичных каналов обслуживания;

Р_n – вероятность нахождения n заявок в системе;

Р_w – вероятность нахождения в очереди.

Для решения используем следующие формулы:

Модель 1.

Модель 2.

Модель 3.

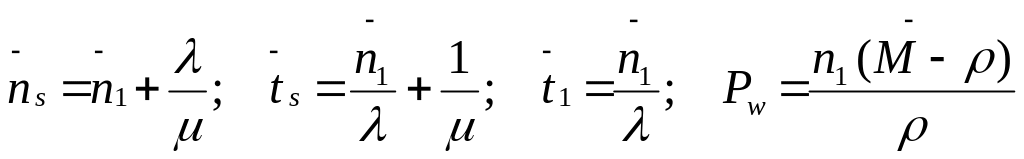
Рассмотрим теперь пример 1, в котором используется модель 1 очередей.

Необходимо проанализировать очередь водителей автомобилей к кассиру для оплаты проезда по 1-полосному мосту. По предварительным оценкам λ=15 автомобилей в час, μ=1 автомобиль в каждые 3 минуты или 20 автомобилей в час. При этих данных:

Средняя загрузка кассира

Среднее количество клиентов, ожидающих в очереди

Среднее количество клиентов в системе

Cреднее время ожидания в очереди

Среднее время ожидания в системе

Подсчитаем вероятность того, что в системе может находиться от 0 до 3 автомобилей . Это есть текущий уровень обслуживания. Да, в среднем в системе будет находиться 3 автомобиля; но число автомобилей в системе в течении времени довольно резко колеблется. Вероятность того, что в системе появится больше 3 автомобилей, равна 1 – 0,685 = 0,315, и того, что будет именно 3 автомобиля, равна 0,106.

Поэтому у фирмы, получающей плату за проезд по мосту, есть стремление повысить текущий уровень обслуживания до 0,95, то есть иметь вероятность, равную 0,95, того, что в очереди не будет скапливаться больше 3 автомобилей. Возникают задачи для реализации этого:

- какая интенсивность обслуживания μ соответствует новому уровню обслуживания?

- какой уровень загрузки ρ кассиры должен быть при этом?

Для их решения рассмотрим уравнение и попробуем путем подбора ρ найти значение корня. При ρ=0,5 левая часть уравнения = 0,9375, а при ρ = 0,45 имеем 0,96. Значит корень 0,45 < ρ < 0,5. При ρ=0,47 левая часть =0,9512. Это значение ρ примем за искомое. Отсюда следующие выводы:

- кассир будет простаивать 53% рабочего времени (при уровне обслуживания 0,685 простой составляет вдвое меньше, 25%).

- новая интенсивность обслуживания кассира будет ,(примерно 1 автомобиль за 2 минуты) что на 60% больше старой (20 ). Ускорение может быть достигнуто путем использования еще одного кассира или уменьшения объема работы кассира (например за счет использования пластиковых карт при расчете).

Пример 2, в котором используется модель 2.

Автосервисная станция заправляет, получая в среднем 0,7$ с машины, и тогда бесплатно моет ее. Либо только моет, получая 0,4$ с 1 машины. Станция работает – 14 час/день. Для работы станция имеет возможность взять в лизинг один из 3 типов моечного оборудования. Число машин для заправки и затем мойки примерно равно числу машин только для мойки. По оценке фирмы клиенты не хотят ждать в очереди на мойку машины больше 5 минут и входящий поток машин на мытье составит 10 шт/час.

Тип	Время мойки 1 автомобиля, минут	Плата в $ день за аренду
1	5	12
2	4	16
3	3	22

Необходимо определить, какой тип моечного оборудования следует выбрать.

Напоминаем, что в этой модели 2 распределение операций обслуживания равномерное! В отличие от модели 1, где оно экспоненциальное, поэтому и формулы разные используются. Равномерность выражается в одинаковом постоянном времени обслуживания для любой машины, так как мойка производится в автоматическом режиме. Фактически очередь машин создается на мойку, а заправят ли в момент ожидания машину, не сказывается на движении очереди, а лишь на потерянных прибылях, если клиент будет нетерпелив и покинет очередь.

Вычислим среднее время ожидания машин в очереди на мойку:

Для оборудования 1 типа μ = 12

Для оборудования 2 типа μ = 15

Использование оборудования 1 типа приведет к потере части клиентов из-за , поэтому оборудование 2 типа предпочтительнее. Но необходимо проверить экономическую целесообразность отказа от оборудования 1 типа – может быть потеря клиентов компенсируется более низкой арендной платой по сравнению с вариантом использования оборудования 2 типа?

Оценим потери прибыли за счет ухода клиентов в 1 варианте. Положим среднее время ожидания в очереди и найдем показатель интенсивности входящего потока клиентов по известному μ = 12 из соотношения . Получим , откуда 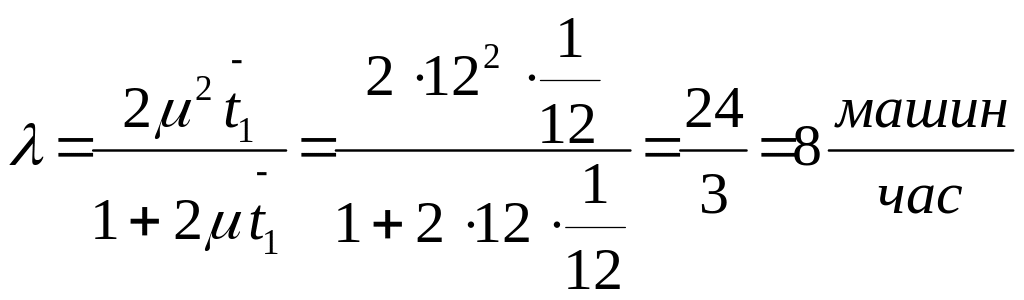вместо ожидаемых 10. Следовательно, фирма теряет и прибыль = (0,7$ за заправку + 0,4$ за мойку) х 14 час = 15,4 . При приобретении оборудования 2 типа вместо 1 типа необходимо платить больше на 4 , но это меньше потерь 15,4 , так как клиенты в среднем будут ждать в очереди 4 минуты, что меньше предельного времени ожидания = 5 мин.

Таким образом следует выбрать 2 тип оборудования, 3 тип более дорогой в аренде и слишком производительный. По этой причине он тоже отвергается.

Пример 3, в котором используется модель 3.

Пусть в отдел запчастей автосервиса приходят слесари с заявками. Служащий в присутствии слесаря заполняет заявку. Слесари приходят произвольно с интенсивностью , служащий заполняет . Оплата труда служащего 6 , слесаря 12 . Необходимо определить оптимальное количество служащих.

При 1 или 2 служащих будут образовываться бесконечно длинные очереди, так как интенсивность обслуживания не превышает интенсивность потока заявок. Воспользуемся готовой таблицей значений среднего количества клиентов в очереди в зависимости от и количества каналов обслуживания М. При и М = 3 получаем слесаря. Процесс установившийся и в среднем такая очередь за 8 час работы слесаря приводит к потерям . Просчитаем длину очереди при наличии 4 служащих. Из той же таблицы при М=4 находим слесаря. Потери за день от ожидания слесаря = 0,1730 х 12 х 8 = 16,61 . Но по сравнению с потерями при 3 служащих экономия = 85,32 – 16,61 = 68,71 . Затраты на оплату дополнительного служащего = 8 час · 6 = 48 . И тогда окончательная экономия = 68,71 – 48 = 20,71 . Следовательно, необходимо использовать 4 служащих.