
Дискретный анализ и теория автоматов. Методические указания для самостоятельной работы студента
.pdf
14 |
1 |
1 |
1 |
0 |
1 |
1 |
|
1 |
|
1 |
1 |
|
15 |
1 |
1 |
1 |
1 |
1 |
0 |
|
1 |
|
1 |
1 |
|
2. |
Скласти |
контактну |
схему, |
яка технічно |
реалізує |
логічну функцію |
||||||
f = ( x y ) (x z y ) u.
Відповідь:
|
u |
|
Uвх |
|
|
y |
x |
Uвих |
|
|
|
x |
|
z |
|
y |
|
|
|
3. Замінити контактну схему комбінаційною схемою на логічних елементах у базисі І-Або-Не.
Відповідь:
u
y
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x y |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
f(x, y, z, u) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
( x y ) (x z y ) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|
|
x z y |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 2
1. Скласти контактну схему за заданими умовами ії роботи. Умови роботи зазначені десятковими номерами 7, 6 і 1 наборів, на яких логічна функція, яку реалізує контактна схема, має значення 1:
f (x1,x2,x3) = f7 (111) = f6 (110) = f1 (001) =1.
Розв’язання
На підставі заданих умов роботи комбінаційної схеми складемо функцію провідності:
|
|
|
|
|
|
|
|
F = x1 x2 x3+ x1 x2 x3 + x1 x2 x3. |
(1) |
||||||
11
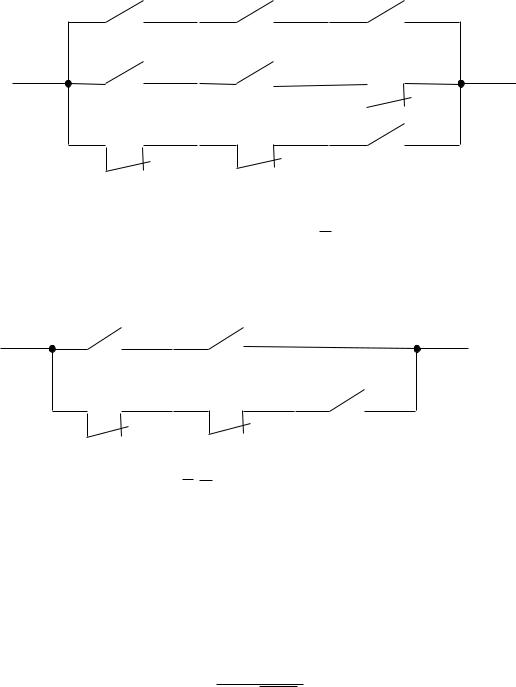
Функція провідності (1) реалізується контактною схемою, яка являє собою паралельне з’єднання трьох гілок:
x1 |
|
x2 |
|
x3 |
||
|
|
|
|
|
|
|
x1 |
|
x2 |
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
x3 |
|||
Оскільки завжди замкнений один із контактів x3 і x3 у двох верхніх гілках, то схему можемо спростити, замінивши ці гілки однією з умовою її роботи f12 (11) = 1:
x1 |
x2 |
|
||
|
|
|
|
x3 |
|
x1 |
|
x2 |
|
Спрощеній контактній схемі відповідає функція провідності |
|
F = x1 x2+ x1 x2 x3. |
(2) |
Зазначимо, що функцію (2) можна також одержати із (1) методом здійснення операції повного склеювання двох перших доданків за змінною x3.
2. Замінити побудовану контактну схему комбінаційною схемою на логічних елементах у заданому базисі І – Не.
Розв’язання
На виході логічної схеми повинне формуватися значення функції (2), яку перетворимо до заданого базису І – Не за законом де Моргана:
|
|
|
|
|
|
|
|
|
|
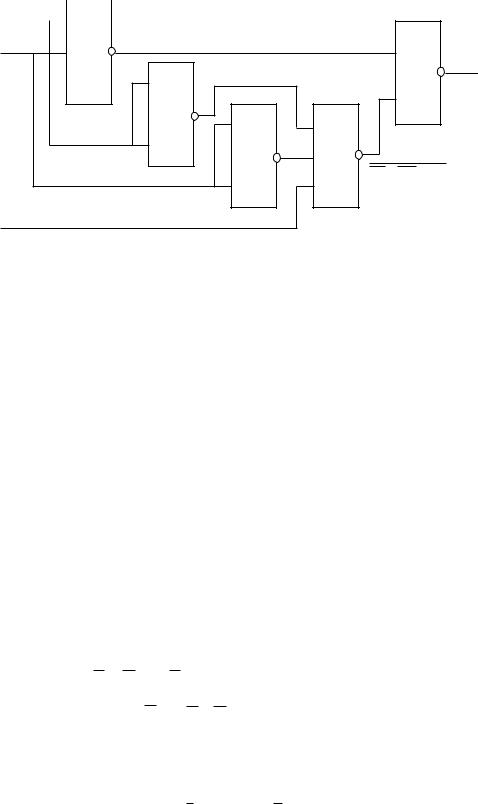
x1 x2+ x1 x2 x3 = (x1x2 )(x1 x2 x3 ) . |
(3) |
||||||||
На підставі формули правої частини (3) складемо логічну схему в базисі І – Не:
12
x1 |
|
|
||||
|
x2 |
|||||
|
|
|
|
x1 |
||
|
|
|
& |
|||
x2 |
|
|||||
F
&
& &
x1 x2 x3
x3
Завдання 3
Логічну функцію f (x1, x2, x3) задано номерами 2, 3, 7 всіх наборів (x1, x2, x3), на яких
f(x1, x2, x3) = 1, тобто f (010)2 = f (011)3 = f (111)7 = 1. Потрібно виконати наступне.
1)Побудувати таблицю істинності функції f (x1,x2,x3).
2)Подати функцію f (x1, x2, x3) формулами в ДДНФ і ДКНФ.
Розв’язання
1. Таблиця істинності
№ |
x1 |
x2 |
x3 |
f (x1, x2, x3) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
1 |
0 |
1 |
3 |
0 |
1 |
1 |
1 |
4 |
1 |
0 |
0 |
0 |
5 |
1 |
0 |
1 |
0 |
6 |
1 |
1 |
0 |
0 |
7 |
1 |
1 |
1 |
1 |
2. На підставі таблиці істинності складемо формули ЛФ у ДДНФ і ДКНФ:
fДДНФ (x1, x2, x3) = ( x1 x2 x3 ) + ( x1 x2 x3) + (x1 x2 x3)
fДКНФ (x1, x2, x3) = (x1+ x2 + x3 ) · ( x1 + x2 + x3) · (x1+ x2 + x3).
Завдання 4
1. Логічну функцію f (x, y, z) = ( x + y z) · (x + y z) + x z подати в ДДНФ і ДКНФ.
Розв’язання
Формулу будь-якої логічної функції можна перетворити в ДНФ, користуючись правилами перетворення формул та законами алгебри логіки, а потім перетворити її в ДДНФ методом розгортання елементарних кон’юнкцій та видалення дублюючих членів.
Перетворимо формулу функції f в ДНФ:
13
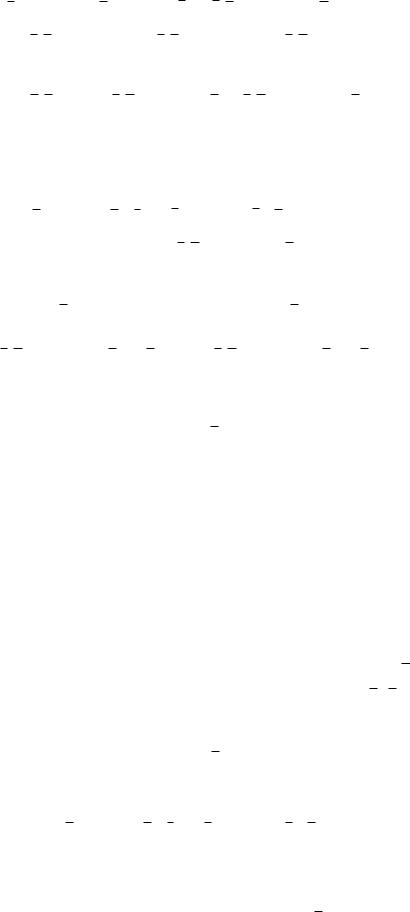
f = ( x + y z) · (x + y z) + x u = x x + x y z + x y z + y y z z + x z = = x y z + x y z + x z = x y z + x z (y + 1) = x y z + x z.
Одержану ДНФ перетворимо у ДДНФ:
fДДНФ = x y z + x z = x y z + x z (y + y ) = x y z + x y z + x y z.
Номери наборів, на яких fДДНФ = 1: (001)1; (101)5; (111)7.
Повна кількість наборів функції f дорівнює 23 = 8. На наборах за номерами (000)0, (010)2, (011)3, (100)4, (110)6 маємо f = 0. Отже, ДКНФ заданої логічної функції має вигляд
fДКНФ = (x + y + z) · (x + y + z) · (x + y + z ) · ( x + y + z) · ( x + y + z).
2. Мінімізуємо в ДНФ функцію fДДНФ = x y z + x y z + x y z за методом Квайна. Перетворюємо ДДНФ логічної функції fДДНФ в СДНФ, базуючись на теоремі Квайна.
Перший та третій доданки функції fДДНФ склеюються за змінною x, тому вони замінюються спільною власною частиною y · z, а конституенти x · y · z і x · y · z склеюються за змінною y, їхньою власною частиною є x z:
x y z + x y z + x y z = y z + x z + x y z + x y z + x y z = y z + x z.
В одержаній формулі всі імпликанти є простими, тому подальше скорочення неможливе. Скорочена ЛФ має вигляд
fСДНФ = x z + y z.
Побудуємо імплікантну таблицю Квайна.
Прості |
|
|
|
Конституенти одиниці |
|||||||
|
|
|
|
|
|
|
|
|
|||
імпліканти |
|
x · y · z |
х · y · z |
х · y · z |
|||||||
|
|
|
|
|
|
|
|
|
|
||
х · z |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y · z |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Із таблиці бачимо, що ядро імплікант містить обидві імпліканти x · z і y · z, оскільки
лише однією з них (як власною частиною) покриваються конституенти x · y · z і x · y · z.
Неядерних імплікант немає. У такому разі тупікова ДНФ єдина, вона і буде мінімальною ДНФ функції f (x, y, z):
fМДНФ = x z + y z.
3. Мінімізуємо в КНФ за методом Квайна функцію
fДКНФ = (x + y + z) · (x + y + z) · (x + y + z ) · ( x + y + z) · ( x + y + z).
Перетворюємо ДКНФ логічної функції fДКНФ в СКНФ, базуючись на теоремі Квайна. Перший та другий сумножники функції fДКНФ склеюються за змінною y, тому вони замінюються спільною власною частиною x + z, другий та третій сумножники склеюються за
змінною z і замінюються спільною власною частиною x + y , перший та четвертий сумножники склеюються за змінною x і замінюються спільною власною частиною y + z,
14

другий та п’ятий сумножники склеюються за змінною x і замінюються спільною власною
частиною y + z, четвертий та п’ятий сумножники склеюються за змінною y і замінюються
спільною власною частиною x + z. Після проведення операцій неповного склеювання та поглинання всіх конституент нуля (оскільки вони всі брали участь у склеюваннях) одержимо:
(x + y + z)· (x + y + z)· (x + y + z )· ( x + y + z)· ( x + y + z) = (x + z)· (x + y )· (y + z)· ( y + z)· ( x +z).
Аналізуючи праву частину цієї рівності, бачимо, що можна понизити ранг сумножників завдяки склеюванням першого з п’ятим за змінною x, третього та четвертого за змінною y. Водночас другий сумножник участі в склеюваннях не бере. В результаті одержимо скорочену форму
fСКНФ = (x + y ) · z · z = (x + y ) · z.
Побудуємо імпліцентну таблицю Квайна ‒ Мак-Класкі.
Прості |
|
Конституенти нуля |
|
||
|
|
|
|
|
|
імпліценти |
111 |
101 |
100 |
011 |
001 |
|
|
|
|
|
|
10 – |
|
|
|
|
|
|
|
|
|
|
|
– –1 |
|
|
|
|
|
Із таблиці бачимо, що ядро імпліцент містить обидві імпліцеанти (x + y ) і z, оскільки
лише однією з них (як власною частиною) покриваються конституенти (x + y + z), (x + y + z ),
( x + y + z) і ( x + y + z). Неядерних імплікант немає. У такому разі тупікова КНФ єдина, вона і буде мінімальною КНФ функції f (x, y, z):
fМКНФ = (x + y ) · z.
Завдання 5
Логічну функцію f (x1, x2, x3, x4) задано номерами 2, 3, 6, 10, 12, 14 всіх наборів, на яких вона набирає значення1. Потрібно виконати наступне:
1) подати функцію f (x1, x2, x3, x4) формулою в ДДНФ;
2) за методом Вейча – Карно мінімізувати в ДНФ одержану в п. 1) функцію f (x1, x2, x3, x4), з натурними позначеннями змінних у розмітці граней таблиці на універсальній карті Карно.
Розв’язання
1) перетворюючи десяткові номери у двійкові, визначимо ці набори: 1100, 1110, 0110, 0011, 1010, 0010. Оскільки це всі набори, на яких функція f (x1, x2, x3, x4) набуває значення1, то в ДДНФ вона набуває вигляду
f (x1, x2, x3, x4) = x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4 ;
2) знайдемо мінімальну ДНФ логічної функції f (x1, x2, x3, x4) з використанням універсальної карти Карно, розміченої за гранями таблиці натурними позначеннями змінних.
15

|
x2 |
|
|
x2 |
|
x1 |
1 |
0 |
0 |
0 |
x3 |
|
|
|
|
||
|
1 |
0 |
0 |
1 |
x3 |
|
|
|
|
|
|
|
1 |
0 |
1 |
|
|
x1 |
0 |
0 |
0 |
0 |
x3 |
|
|
|
|
|
|
|
x4 |
|
x4 |
x4 |
|
|
|
|
|
Як випливає з побудови контурів за єдиним варіантом, тупикова ДНФ також єдина, тому мінімальна ДНФ дорівнює цій тупиковій та має вигляд
FДНФmin (A, B, C, D) = x3 x4 + x1 x2 x4 + x1 x2 x3 .
Завдання 6
Логічну функцію f (x1, x2, x3, x4) задано номерами 1, 4, 9, 11, 14, 15 усіх наборів (x1, x2, x3, x4), на яких вона набуває значення 1. Потрібно виконати наступне:
1) подати функцію f (x1, x2, x3, x4) формулою в ДДНФ;
2) за методом Вейча – Карно мінімізувати в КНФ одержану в п. 1) функцію f (x1, x2, x3, x4), з позначеннями змінних із бази функції в узагальнених кодах під час розмітки граней таблиці на універсальній карті Карно.
Розв’язання
1) перетворюючи десяткові номери у двійкові, визначимо ці набори: 0001, 0100, 1001, 1011, 1110, 1111. Оскільки це всі набори, на яких функція f (x1, x2, x3, x4) приймає значення1, то в ДДНФ вона набуває вигляду:
f (x1, x2, x3, x4) = x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4 + x1 x2 x3 x4+x1 x2 x3 x4 + x1 x2 x3 x4 ;
2) знайдемо мінімальну КНФ логічної функції f (x1, x2, x3, x4) з використанням універсальної карти Карно, розміченої за гранями таблиці парами змінних в узагальнених кодах.
У нашому разі побудова контурів можлива у трьох варіантах, як показано нижче.
|
|
|
|
|
Варіант 1 |
|
|
|
|
|
|
|||
x3x4 |
00 |
01 |
|
|
11 |
|
|
|
10 |
|
||||
x1x2 |
|
|
|
|
|
|
||||||||
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
0 |
|
|
|
0 |
|
|||
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
0 |
|
|
1 |
|
|
|
1 |
|
||||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
1 |
|
|
1 |
|
|
|
0 |
|
||||
Одержано 2 контури з 4 клітинок і 2 контури з 2 клітинок (у наборах контурів виділені спільні значення змінних):
16
1) 0000 |
2) 0011 |
3) 0101 |
|
4) 1100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0010 |
0010 |
0111 |
|
|
|
|
|
1101 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1000 |
0111 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1010 |
0110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цим контурам відповідають конституенти нуля, кон’юнктивне сполучення яких являє |
||||||||||||||||||||||||||||
собою тупикову КНФ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в узагальнених кодах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f тiп (x1, x2, x3, x4) = |
(–1 – 1) · (1– 0 –) · (10 – 0) · (001 – ), |
|
|||||||||||||||||||||||||
|
КНФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у натурних позначеннях змінних |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f тiп (x1, x2, x3, x4) = (x2 + x4) · (x1+ x |
) · (x1+ x |
2 |
+ x |
4 |
) · ( x |
+ x |
2 |
+ x3). |
(1) |
|||||||||||||||||||
КНФ |
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Варіант 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x3x4 |
00 |
|
|
|
|
01 |
|
|
|
11 |
|
10 |
|
|
|
|
|
|
||||||||
|
|
x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
Одержано 2 контури з 4 клітинок і 2 контури з 2 клітинок (у наборах контурів виділені спільні значення змінних):
1) 0000 |
2) 0011 |
3) 1100 |
4) 0101 |
0010 |
0010 |
1000 |
1101 |
1000 |
0111 |
|
|
1010 |
0110 |
|
|
Цим контурам відповідають конституенти нуля, кон’юнктивне сполучення яких являє
собою тупикову КНФ: |
|
|
|
|
|
|
|
|
|
|
|
f туп (x1, x2, x3, x4) = (x2 + x4) · (x1 + |
|
|
|
|
|
|
|
|
|
|
|
x |
) · ( x + x3 + x4) · ( x |
2 |
+ x3 + x |
4 |
). |
(2) |
|||||
КНФ |
3 |
1 |
|
|
|
|
|
|
|||
Варіант 3
17
x3x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1x2 |
00 |
01 |
|
|
11 |
|
|
10 |
|
||||
00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0 |
|
|
0 |
|
|||||
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
1 |
|
||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
1 |
|
|
1 |
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одержані 2 контури з 4 клітинок і 2 контури з 2 клітинок (у наборах контурів виділені спільні значення змінних):
1) 0000 |
2) 0011 |
3) 1100 |
4) 0101 |
0010 |
0010 |
1101 |
1101 |
1000 |
0111 |
|
|
1010 |
0110 |
|
|
Цим контурам відповідають конституенти нуля, кон’юнктивне сполучення яких являє собою тупикову КНФ:
f туп (x1, x2, x3, x4) = (x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x4) · (x1 |
+ x |
) · ( x |
+ x |
2 |
+ x3) · ( x |
2 |
+ x3 + x |
4 |
). |
(3) |
||||||
КНФ |
|
3 |
1 |
|
|
|
|
|
|
|
|
|||||
За мінімальну КНФ слід прийняти функцію (2) з кількістю символів на 1 менше ніж у формулах функцій (1) і (3).
3.3 Розділ 3. Елементи теорії графів
Завдання 1
Граф Gn,m = (V, E) з вершинами v1, v2,…, v5 V і ребрами e1, e2,…, e7 E задано переліком неорієнтованих ребер ei = (vi, vk), а саме:
е1 = (v1, v2); е2 = (v2, v2); е3 = (v2, v3); е4 = (v3, v4); е5 = (v4, v5); е6 = (v5, v1); е7 = (v5, v3);
Потрібне виконати наступне:
1)накреслити діаграму графа та визначити, чи відповідає цей граф кожному з таких означень: скінченний, неорієнтований, орієнтований, змішаний, порожній, тривіальний, нуль-граф, повний, мультиграф, граф Бержа, псевдограф, простий, помічений, зважений;
2)визначити степені всіх вершин графа;
3)скласти список суміжностей вершин графа;
4)скласти список інциденцій ребер графа;
5)скласти матрицю суміжностей графа;
6)скласти матрицю інциденцій графа.
Розв’язання
1) діаграма графа
18

|
|
|
v1 |
|
|
|
e6 |
e1 |
|
|
|
|
|
e2 |
v5 |
|
|
|
|
e5 |
|
e7 |
v2 |
|
|
|
|
||
|
|
|
e3 |
|
|
|
|
|
|
v4 |
|
e4 |
|
v3 |
|
|
|
|
|
Цей граф не є: орієнтованим, змішаним, порожнім, тривіальним, нуль-графом, повним, простим, зваженим, мультиграфом.
Цей граф є: скінченним, неорієнтованим, графом Бержа, псевдографом, поміченим;
2) степені вершин графа:
deg (v1) = 2; deg (v2) = 4; deg (v3) = 3; deg (v4) = 2; deg (v5) = 3.
3) |
список суміжностей вершин графа |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vi: |
|
|
|
v1 |
|
|
|
v2 |
|
v3 |
v4 |
v5 |
|
||
|
|
|
S(vi) ={…}: |
|
v2, v5 |
|
v1, v3 |
|
v2, v4, v5 |
v3, v5 |
v1, v3, v4 |
|
|||||||||
4) |
список інциденцій ребер графа |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei: |
|
e1 |
|
|
|
e2 |
|
|
|
e3 |
|
e4 |
|
e5 |
e6 |
|
e7 |
||
|
|
vi, vk : |
v1, v2 |
|
|
v2, v2 |
|
|
v2, v3 |
|
v3, v4 |
|
v4,v5 |
v5, v1 |
|
v5, v3 |
|||||
5) |
матриця суміжностей графа |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6) матриця інциденцій графа
|
|
|
e1 |
e2 |
e3 |
e4 |
e5 |
e6 |
e7 |
|
v1 |
|
|
|
0 |
0 |
0 |
0 |
1 |
0 |
|
|
|
1 |
|
|||||||
v2 |
|
|
1 |
2 |
1 |
0 |
0 |
0 |
0 |
|
v3 |
|
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
v4 |
|
|
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
v5 |
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Завдання 2
19
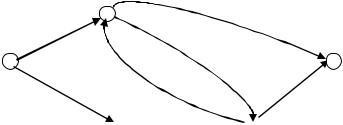
Орграф Gn,m = (V, E) з вершинами v1, v2, …, v5 V і дугами e1, e2, …, e7 E задано переліком дуг ei = (vi, vk), вагами вершин hi, I = 1, …, n та дуг pi, i = 1, …, m, а саме:
n = 5; h1 = 8, h2 = 12, h3 = 5, h4 = 15, h5 = 10;
m = 7; e1 = (v1, v2), p1 = 12; e2 = (v1, v3), p2 = 10; e3 = (v2, v4), p3 = 15; e4 = (v2, v5), p4 = 12; e5 = (v4, v2), p5 = 20; e6 = (v3, v4), p6 = 10; e7 = (v4, v5), p7 = 15.
Потрібне виконати наступне:
1)накреслити діаграму графа та визначити, чи відповідає цей граф кожному з таких означень: мультиграф, псевдо граф;
2)визначити степені, напівстепені виходу і заходу всіх вершин графа. Які з вершин графа є витоком та стоком (за наявністю);
3)вважаючі граф вершинно зваженим, скласти список суміжностей та ваг вершин
графа;
4)вважаючі граф реберно зваженим, скласти список інциденцій та ваг дуг графа;
5)скласти матрицю суміжностей графа;
6)скласти матрицю інциденцій графа;
7)вважаючи граф реберно зваженим, скласти матрицю ваг дуг графа;
8)вважаючи граф вершинно зваженим, скласти матрицю ваг вершин графа.
Розв’язання
1) діаграма графа
v2
e4
e1
v1 |
e3 |
v53 |
e53
e73
e2

 v4
v4
v3 e63
Цей граф не є псевдографом. Цей граф є мультиграфом.
2) степені, напівстепені заходу, напівстепені виходу вершини графа
vi |
v1 |
v2 |
v3 |
v4 |
v5 |
deg (vi) |
2 |
4 |
2 |
4 |
2 |
deg + (vi) |
0 |
2 |
1 |
2 |
2 |
deg ‒ (vi) |
2 |
2 |
1 |
2 |
0 |
Вершини v1 та v5 є відповідно витоком та стоком.
3) список суміжностей та ваг вершин графа
vi: |
v1 |
v2 |
v3 |
v4 |
v5 |
S(vi) = {…}: |
v2, v3 |
v1, v4, v5 |
v1, v4 |
v2, v3, v5 |
v2, v4 |
hi: |
8 |
12 |
5 |
15 |
10 |
|
|
20 |
|
|
|
