
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НОВОСИБИРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Физический факультет
Кафедра биомедицинской физики
Чирятьева Александра Евгеньевна
РЕФЕРАТ НА ТЕМУ
Хаос в биологических системах
Введение в молекулярную биофизику, 3 курс, группа №14315
Преподаватель:
_______________А. А. Ломзов
«___» _______________2016 г.
Оглавление
Введение 3
Хаос в биологических системах 6
Экология и популяции 6
Органы и ткани 6
Клеточно-молекулярный уровень 8
Заключение 10
Список литературы 11
Введение
Вторая половина XX века ознаменовалась бурным развитием нового научного направления – теории хаоса, расположившейся на стыке математики, физики, астрономии, химии, биологии. С развитием методов компьютерного моделирования исследование хаоса превратилось в самостоятельную область знания. В частности, биологи получили в свое распоряжение методы математической физики для описания изменений, происходящих в биологических системах различного рода.
Появление непредсказуемости в самоорганизации сложных систем неизбежно, поэтому необходимо определить понятие хаоса. Как правило, под хаосом подразумевается полная дезорганизация системы, зависящей от случайной последовательности событий. Математики рассматривают хаос как элемент формальной теории нелинейных систем. Детерминированный (динамический) хаос – явление, которому подвержены динамические системы при наличии неустойчивости по отношению к начальным условиям. Это понятие позволяет изучать формально детерминированные процессы, прогнозируемые лишь в ограниченный промежуток времени, поскольку не существует абсолютно упорядоченных и предсказуемых систем, равно как не существует и полностью случайных, нерегулярных систем.
Эволюция системы может быть описана математически с помощью её фазового портрета – совокупности кривых последовательных состояний процесса в фазовом пространстве. Положение системы определяется, в общем случае, аттрактором – множеством точек фазового пространства, к которым стремятся все траектории системы. В качестве аттрактора может выступать неподвижная точка, замкнутая кривая, либо так называемый хаотический (странный) аттрактор (рис. 1). Именно странные аттракторы являются математическим образом детерминированных непериодических процессов, происходящих в нелинейных системах.

Рис. 1. Построение временных последовательностей (вверху) и траекторий в фазовом пространстве (внизу) для различных систем [1]
В фазовом пространстве хаотического аттрактора прогнозируемость положения точки ограничена, так как с течением времени траектории близких пробных точек расходятся по ветвям аттрактора настолько, что возможным становится только статистическое прогнозирование в пределах системы аттрактора [1].
В качестве примера хаотического аттрактора рассмотрим фазовый портрет системы Лоренца.
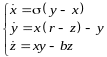
Эта трехмерная динамическая система автономных нелинейных дифференциальных уравнений первого порядка была представлена в 1963 году Эдвардом Лоренцем, который занимался прогнозированием метеорологических явлений. Проводя численное построение фазового портрета системы, Лоренц обнаружил асимптотически устойчивое множество, имеющее сложную топологическую структуру, к которому притягиваются все траектории – аттрактор Лоренца.
На рисунке 2 показан аттрактор Лоренца и расхождение траекторий 10 000 пробных точек. Можно заметить, что движение точек становится непредсказуемым: конечное состояние системы может находиться в любой точке в системе аттрактора [2].

Рис. 2 Расхождение фазовых траекторий 10 000 точек в системе аттрактора Лоренца [2]
Таким образом, под хаосом следует понимать не беспорядок в системе, но ограниченную её предсказуемость. В биологических системах наблюдаемая случайность многих событий также обусловлена влиянием динамического хаоса. Непредсказуемое поведение демонстрируют биосистемы на всех уровнях организации – от биосферного до молекулярного.
