15. Дать определение понятия «индекс», изложить правила построения индексов, составить классификацию индексов, выделить условия применения индексов
«Индекс» в переводе с латинского - указатель или показатель. В статистике индексами называют относительные показатели, характеризующие изменение сложных общественных явлений, элементы которых не поддаются непосредственному суммированию. Индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя.
Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов (например, индекс цен равен 1,1 или 110%, означает, что цены возросли на 10%).
В целом, индексный метод направлен на решение следующих задач:
1) характеристика общего изменения уровня сложного социально-экономического явления;
2) анализ влияния каждого из факторов на изменение индексируемой величины путем элиминирования воздействия прочих факторов;
3) анализ влияния структурных сдвигов на изменение индексируемой величины и др.
Классификация индексов
По степени охвата явления индексы бывают:
индивидуальные – характеризуют изменения отдельных элементов сложного явления.
Индивидуальный
индекс цены имеет вид
– характеризует изменение цены одного
определенного товара в текущем периоде
по сравнению с базисным;
общие – они чаще используются в экономических расчетах.
Общий
индекс характеризует изменение
какого-либо сложного явления в целом.
Например, индекс себестоимости продукции
радиоэлектронной промышленности:
.
В зависимости от базы сравнения различают цепные индексы (с переменной базой сравнения) и базисные (с постоянной базой сравнения).
В зависимости от характера и содержания индексируемой величины различают индексы количественных показателей (индекс физического объема продукции) и индексы качественных показателей (индексы себестоимости, цены, трудоемкости, выработки).
В зависимости от методологии расчета различаютагрегатные индексы и средние индексы.
При
построении агрегатных индексов
количественных показателей индексируемая
величина в числителе записывается с
символом «1», в знаменателе с символом
«0», а веса – на уровне базисного периода,
т.е. в числителе и знаменателе с символом
«0».Например,
общий агрегатный индекс физического
объема продукции:
.
При построении агрегатных индексов качественных показателей индексируемая величина в числителе записывается с символом «1», в знаменателе с символом «0», а веса (количественный показатели) – на уровне базисного периода, т.е. в числителе и знаменателе с символом «1».
Общий
агрегатный индекс цены :
.
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.
Приисчислении средних индексов используются 2 формы средних: средняя арифметическая и средняя гармоническая.К индексам средних величин относят: индекс переменного состава, индекс фиксированного состава и индекс структурных сдвигов.
16. Высказать общее суждение о средних индексах, раскрыть сущность индекса переменного состава, индекса постоянного состава и индекса структурных сдвигов, расшифровать их взаимосвязь, охарактеризовать индексный метод выявления влияния отдельных факторов на результат
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов.
Приисчислении средних индексов используются 2 формы средних: средняя арифметическая и средняя гармоническая.
Величина агрегатного индекса физического объема ( ) зависит от индивидуальных индексов физического объема, так как общее изменение является результатом изменения объема продукции каждого вида. Общий результат зависит также от удельного веса каждого вида продукции в общем объеме.
Общий индекс физического объёма, построенный на базе индивидуальных индексов принимает форму среднего арифметического или среднего гармонического индекса.
Если
известны индивидуальные индексы
физического объема (
)
и стоимость продукции в базисном периоде
(
),
то мы можем получить средний
арифметический индекс
физического объёма:
.
Соотношение
показывает долю данного вида продукции
в общем объеме продукции базисного
периода (
).
Средний арифметический индекс физического
объема примет вид:
.
Если
известна стоимость продукции отчетного
периода в неизменных ценах и индивидуальные
индексы физического объёма, можно
исчислить средний
гармонический индекс физического
объема:
.
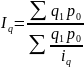К индексам средних величин относят:
Индекс переменного состава – выражает соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Например, индекс себестоимости переменного состава продукции одного и того же вида рассчитывается:
.
Величина
индекса переменного состава себестоимости
зависит от уровнясебестоимости продукции
на отдельных предприятиях и от изменения
удельных весов объема продукции,
выпускаемыми отдельными предприятиями.
2)Индекс
постоянного (фиксированного) состава
- индекс исчисленный с весами на уровне
одного какого-либо периода и показывающий
изменение только индексируемой величины.
Индекс фиксированного состава
себестоимости продукции:
.
Характеризует изменение себестоимости под влиянием изменения себестоимости на каждом предприятии.
3) Индекс структурных сдвигов характеризует влияние изменения только структуры изучаемого явления на динамику среднего уровня этого явления. Например, индекс изменения среднего уровня себестоимости определяется по формуле:
.
Характеризует изменение средней себестоимости продукции под влиянием изменения структуры выпускаемой продукции.
Взаимосвязь между индексами: индекс переменного состава равен произведению индекса фиксированного состава на индекс структурных сдвигов.
Используя индексы средних показателей, можно найти не только их относительное изменение, но и определить абсолютное изменение уровня среднего показателя в целом и за счёт каждого из факторов: а) за счёт непосредственного изменения уровней осредняемого признака и б) за счёт изменения структуры. Для этого необходимо из числителя соответствующего индекса приведённой системы индексов вычесть его знаменатель.