МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра физики
ОТЧЕТ
Лабораторная работа по курсу "Общая физика"
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Выполнил студент
_______________________
2009
1. ЦЕЛЬ РАБОТЫ
Целью данной работы является изучение работы колебательного контура, свободных затухающих электромагнитных колебаний и их характеристик.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
С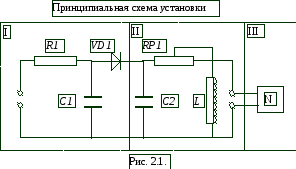 хема
установки представлена на рис. 2.1..
Колебания в контуре II возбуждаются с
помощью генератора импульсного
напряжения, вырабатываемого в контуре
I, собранного на резисторе R1
, емкости
C1
и диоде VD1
( в качестве генератора импульсного
напряжения можно использовать стандартный
генератор импульсов или генератор
релаксационных колебаний).
хема
установки представлена на рис. 2.1..
Колебания в контуре II возбуждаются с
помощью генератора импульсного
напряжения, вырабатываемого в контуре
I, собранного на резисторе R1
, емкости
C1
и диоде VD1
( в качестве генератора импульсного
напряжения можно использовать стандартный
генератор импульсов или генератор
релаксационных колебаний).
Схема смонтирована на съемной панели лабораторного макета. В качестве резистора RP1 в колебательном контуре II используется переменное сопротивление, максимальное значение которого RP1 = 400 Ом устанавливается поворотом ручки потенциометра по часовой стрелке в крайнее положение. При повороте ручки против часовой стрелки в крайнее положение значение сопротивления RP1 = 0. В этом случае активное сопротивление колебательного контура R складывается из сопротивления соединительных проводов контура и активного сопротивления катушки индуктивности. Возбуждение контура производится периодически от генератора импульсного напряжения I, регистрируются колебания на осциллографе III. Каждый импульс, подаваемый с генератора на колебательный контур, возбуждает один цуг колебаний.
Измерения амплитуды и периода колебаний осуществляются непосредственно с помощью осциллографа.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Значения логарифмического декремента затухания:
![]() ; (3.1)
; (3.1)
где
i=1…Nr – номера значений сопротивления RP,
j=1…Np – номера пар амплитуд,
Nr – количество значений сопротивления RP.
Среднее значение логарифмических декрементов затухания:
![]() (3.2)
(3.2)
где Np=Nd-1 – количество пар амплитуд,
Nd – количество измерений при неизменном сопротивлении RP.
Натуральные логарифмы отношений первой амплитуды к последующим:
![]() (3.3)
(3.3)
где
k=1…Nr – порядковый номер эксперимента при неизменном сопротивлении RP,
n=1…Nd – номер измерений при неизменном сопротивлении RP .
Периоды затухающих колебаний определяются как среднее арифметическое измеренных периодов:
![]() (3.4)
(3.4)
Метод наименьших квадратов для построения прямых по экспериментальным точкам:
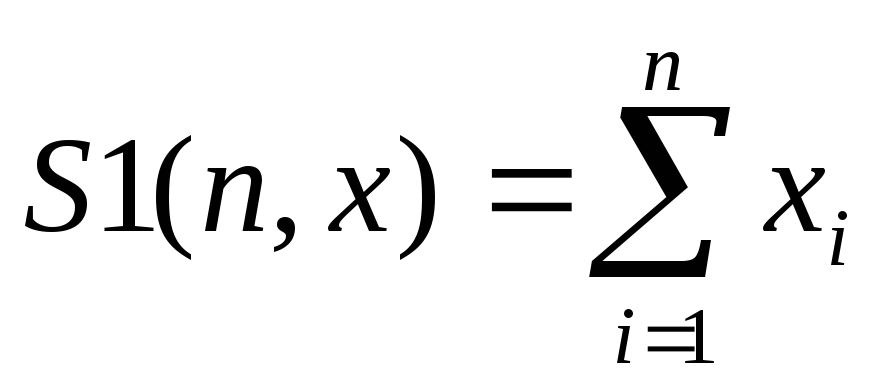 (3.5)
(3.5)
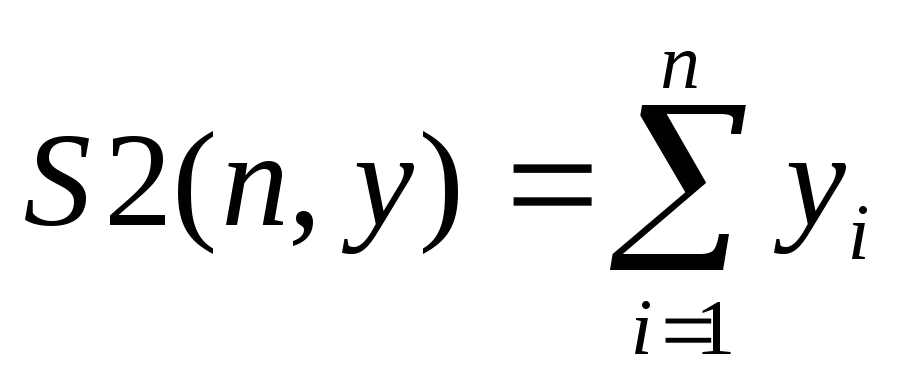 (3.6)
(3.6)
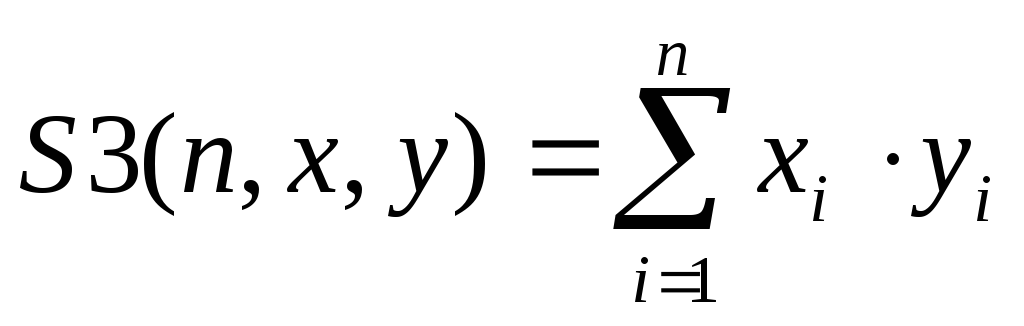 (3.7)
(3.7)
 (3.8)
(3.8)
 (3.10)
(3.10)
![]() (3.11)
(3.11)
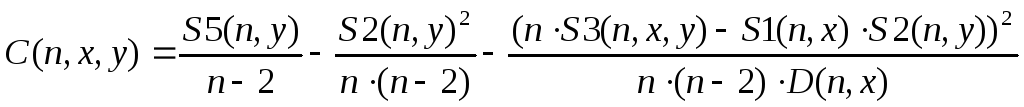 (3.12)
(3.12)
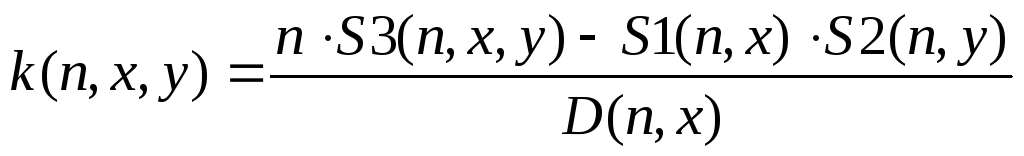 (3.13)
(3.13)
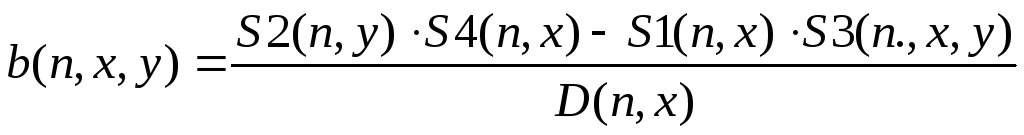 (3.14)
(3.14)
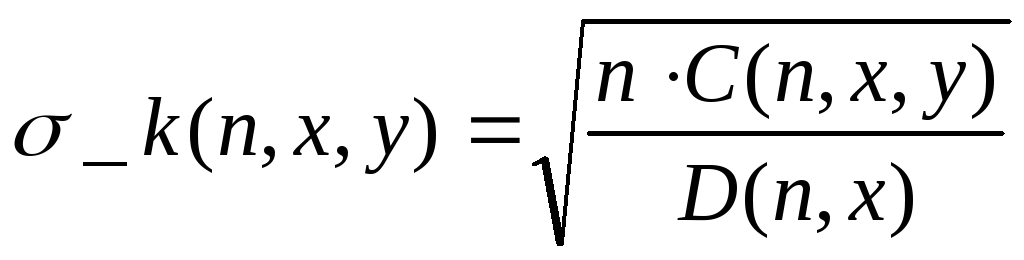 (3.15)
(3.15)
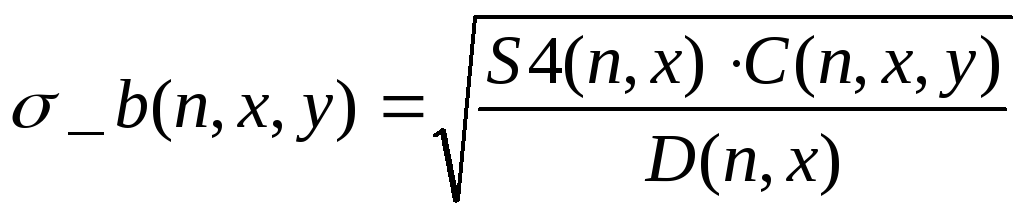 (3.16)
(3.16)
Значение коэффициента затухания контура:
δ = R/2L ; (3.17)
где R – сопротивление контура;
L – индуктивность контура.
Cуммарное активное сопротивление проводников Rx (на основании соотношения 3.5):
Rx = 2L× δ1 (3.18)
Частота собственных незатухающих колебаний контура:
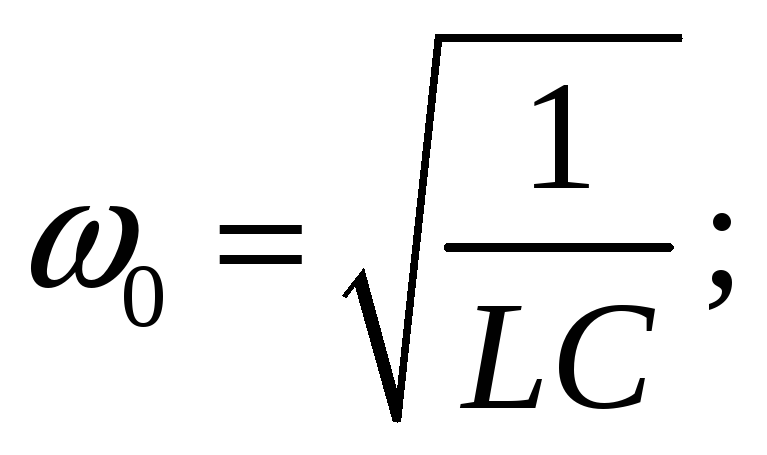 (3.19)
(3.19)
где
С – емкость контура;
L – индуктивность контура.
Частота свободных затухающих колебаний:
![]() (3.20)
(3.20)
где ω0 – частота собственных незатухающих колебаний;
δ – коэффициента затухания .
Период колебаний:
![]() ; (3.21)
; (3.21)
где ω – частота свободных затухающих колебаний.
С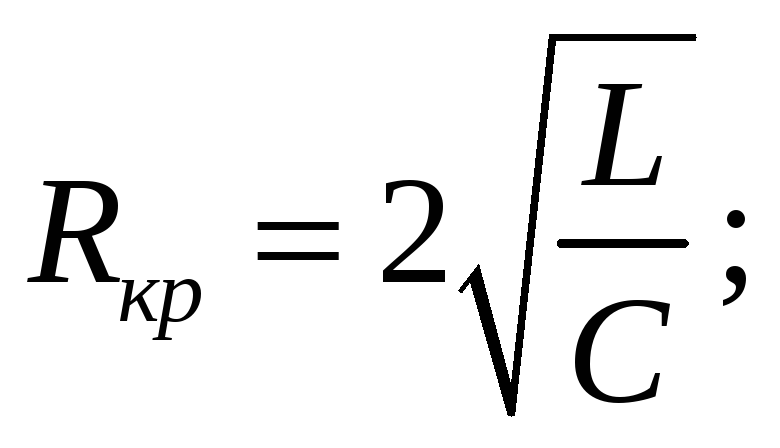 опротивление
контура, при котором наступает
апериодический процесс (из условия ω0
= δ):
опротивление
контура, при котором наступает
апериодический процесс (из условия ω0
= δ):
(3.22)
В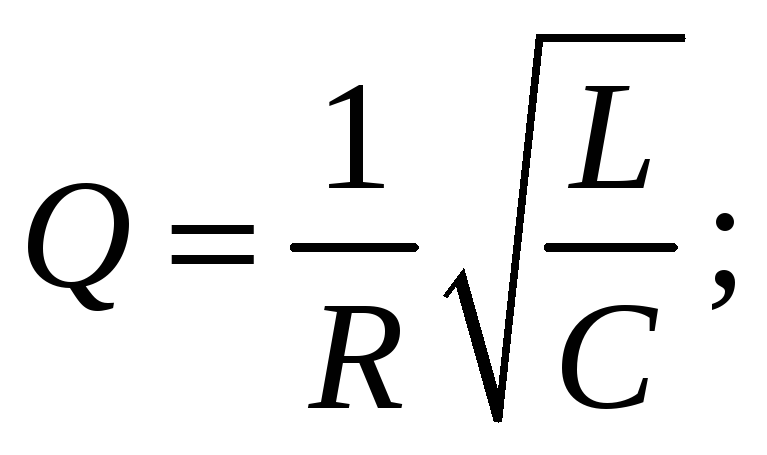 еличина
добротности контура:
еличина
добротности контура:
(3.23)
4. Результаты работы и их анализ
Макет 19.
Измеренные значения и результаты их обработки приведены в таблице 4.1.
Запишем данные из журнала измерений в матрицы. В первые строки матриц U и T5 записываются измеренные значения амплитуд (опыты №№1-5) и периодов (опыты №№6-10) соответственно при сопротивлении RP1=0 Ом , во вторые строки данных матриц записываются амплитуды (опыты №№11-15) и периоды (опыты №№16-20) при сопротивлении RP2=400 Ом.
![]()
![]()
По формуле (3.1) вычисляем логарифмические декременты затухания для каждой пары измеренных амплитуд:
![]()
Средние значения логарифмических декрементов для двух случаев(3.2):
![]()
Натуральные логарифмы отношений первой амплитуды к последующим для двух случаев (3.3)


Периоды затухающих колебаний для двух случаев(3.4)
![]()
Экспериментальные данные и результаты их обработки запишем в таблицу.
Таблица 4.1
Результаты прямых и косвенных измерений.
|
Значение активного сопротивления контура R |
Номер измеряемой амплитуды n |
Значение амплитуды Un, мм (дел.) |
Значение логариф-мического декремента затухания |
Среднее значение <> |
|
Период затухающих колебаний T, c |
|
RP1=0 |
1. 2. 3. 4. 5. |
0,793 0,683 0,586 0,498 0,434 |
0,149 0,153 0,163 0,138 |
0,151 |
0 0,149 0,303 0,465 0,603 |
2,374x10-3 |
|
RP2=400 |
1. 2. 3. 4. 5. |
0,254 0,152 0,0807 0.0484 0,0277 |
0.513 0,663 0,511 0,558 |
0,554 |
0 0,513 1,147 1,658 2.216 |
9,73x10-4 |
Построение графиков.
При построение графиков используется время, выраженное в периодах :
![]()
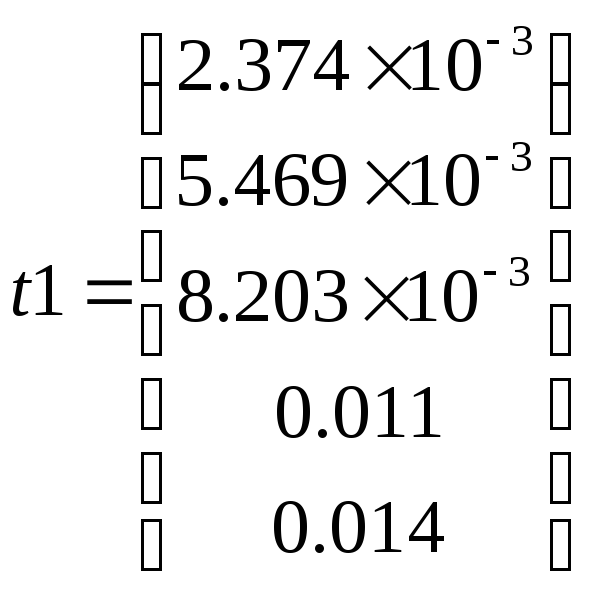
![]()

Применим метод наименьших квадратов для построения прямых по экспериментальным точкам (3.5)-(3.16):
![]() с-1
– угловой коэффициент
с-1
– угловой коэффициент
1-й прямой
![]() –
отрезок, отсекаемый
–
отрезок, отсекаемый
1-й прямой от оси OY
![]() с-1
– угловой коэффициент
с-1
– угловой коэффициент
2-й прямой
![]() –
отрезок, отсекаемый
–
отрезок, отсекаемый
2-й прямой от оси OY
Абсолютные погрешности вычисления параметров прямых линий:
![]() с-1
с-1
![]()
![]() с-1
с-1
![]()
С учётом полученных параметров записываем уравнения прямых.
![]()
![]()
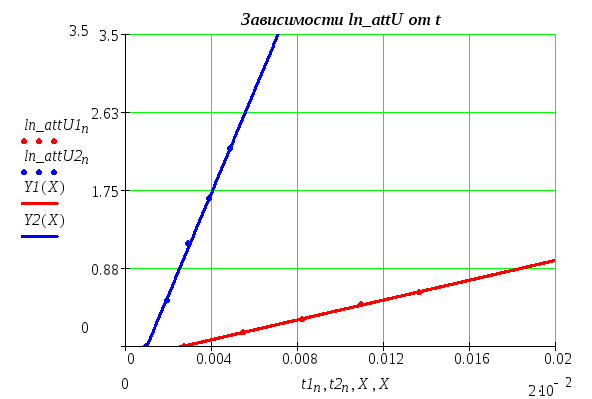 График
4.2. Зависимости ln_attU
от
t
График
4.2. Зависимости ln_attU
от
t
Найденные методом наименьших квадратов угловые коэффициенты прямых являются коэффициентами затухания:
![]()
С использованием (3.17) и учётом, что в первом случае RP = 0, можно записать
![]()
![]()
и тогда, разрешив эту систему, составленную из двух соотношений, относительно L, получим:
![]() Гн индуктивность
контура.
Гн индуктивность
контура.
С использованием известного L из первого соотношения находится суммарное активное сопротивление проводников:
![]() Ом
Ом
С учетом емкости конденсатора С=0.047x10-6 A и использованием (3.19) вычисляем собственная частота контура:
![]() с-1
с-1
Получим частоты затухающих колебаний (3.20):
![]() с-1
с-1
Аналитически периоды затухающих колебаний для двух случаев находятся по (3.21):
![]() с
с
Отличия в процентах измеренных и вычисленных значений периодов

![]()
Сопротивление, при котором наступает апериодический процесс, называется критическим и определяется по (3.22):
Rkp=5.735x103 Ом
Так как mean<1 и приблизительно равны , то для вычисления добротности двух исследуемых контуров можно использовать (3.23)
![]()