13. Два электрона с кинетическими энергиями е1 и е2 движутся в магнитном поле, перпендикулярно направлению поля. Найти отношение их периодов обращения и радиусов траекторий.

Кинетическая энергия движущегося электрона равна:

(5.1)

где m, v – масса и скорость электрона.

Из выражения для 5.1 определим скорость электрона:

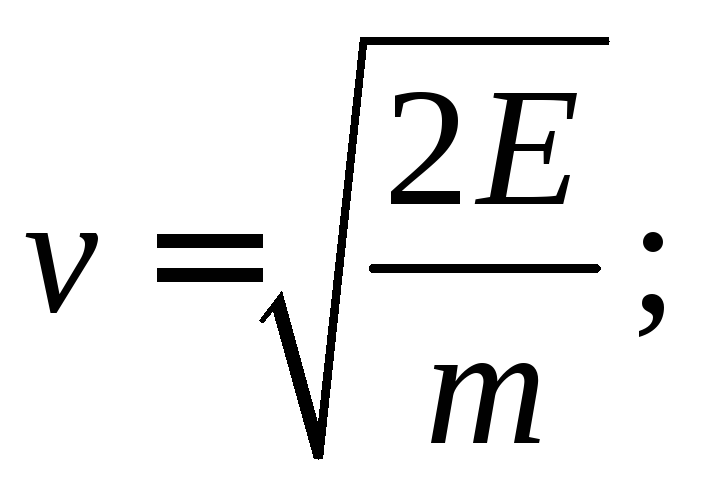(5.2)

Если электрон движется в однородном магнитном поле под действием силы Лоренца, а его скорость лежит в плоскости, перпендикулярной вектору магнитной индукциито электрон будет двигаться по окружности радиуса:(5.3)

где e – заряд электрона.

Из выражения 5.3 следует, что радиус кривизны траектории электрона пропорционален его скорости. На основании выражения 5.3 с учетом значения скорости электрона (5.2) найдем отношение радиусов траекторий движения электронов:

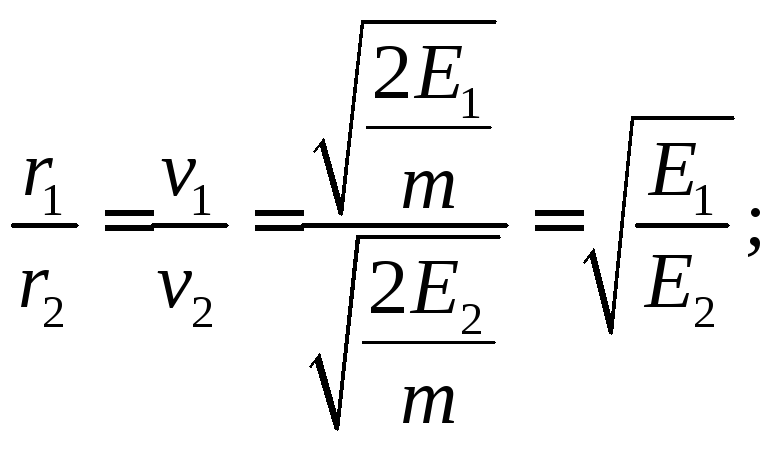
Период обращения частицы в однородном магнитном поле равен:

Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории r.

Следовательно, периоды обращения электронов будут равны: T₁ = T₂.

14. Определить частоту вращения (циклотронную частоту) частицы массы m и зарядом q в магнитном поле индукции b.

Е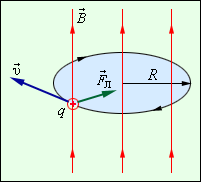сли заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скоростьлежит в плоскости, перпендикулярной вектору магнитной индукциито частица будет двигаться по окружности радиуса:(5.4)

где m,v,q – масса, скорость и заряд частицы.

 

Сила Лоренца в этом случае играет роль центростремительной силы (рис. 5.5).

Период обращения частицы в однородном

магнитном поле равен:

Рисунок 5.5

Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории r.

Угловая скорость движения заряженной частицы по круговой траектории:

(5.5)

Подставим в полученное выражение (5.5) выражение для радиуса траектории частицы (5.4), получим:

называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).

15. Выполняется ли принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях?

Движение частицы, находящейся в электромагнитном поле, описывается следующим уравнением.

Второй закон Ньютона: 

Заряженная частица, обладающая зарядом q, движется в электромагнитном поле согласно этому уравнению. Видим, что сила, действующая на частицу со стороны электромагнитного поля, определяется двумя векторными полями: поле называется напряжённостью электрического поля, поле- индукция магнитного поля. Они разделены, потому что влияние их на частицу различны. Полене содержит никаких характеристик частицы кроме заряда. Еслиv = 0, то второе слагаемое обращается в ноль. Это означает, что магнитное поле действует только на движущиеся частицы. Неподвижные заряды не чувствуют магнитного поля.

Следовательно, принцип независимости движения для заряженных частиц, движущихся одновременно в электрическом и магнитном полях, выполняется.