2.6.3 Уравнение регрессии

Если зависимость между величинами Х и Y будет установлена и выражена формулой, то ее можно использовать для соответствующей организации измерений и обработки их результатов.

Уравнение линейной регрессии Y на Х, отражающее прямолинейную корреляционную связь между переменными Х и Y, имеет вид:

,

(2.32)

где  — коэффициент регрессии Y на Х, вычисляемый по формуле

.	(2.33)

Задача 2.1 В таблице 2.2 приведены результаты измерений длин линий D_i (в км) и абсолютные значения ошибок _i (в см), их сопровождающих.

Вычислить коэффициент корреляции; с вероятностью 0,90 оценить его надёжность и составить уравнение регрессии  на D.

1.Прежде чем решать задачу, прибегают к графическому изображению точек  .

Рис. 2.2 — Прямая регрессии

График на рис. 2.2 указывает на наличие корреляции между D и .

Решение. Вычисление необходимых сумм, а также контроли вычислений поместим в таблице 2.2.

Таблица 2.2
№ п/п	, Км	, См						Примечания
1	8,7	6,8	+4,0	+3,0	16,00	9,00	+12,00	1) ; ; . ; ; . ; . Контроли: . Контроли выполнены.
2	3,7	3,1	–1,0	–0,7	01,00	0,49	0+0,70
3	6,0	3,8	+1,3	–0,0	01,69	0,00	0+0,00
4	3,3	2,9	–1,4	–0,9	01,96	0,81	0+1,26
5	5,1	4,1	+0,4	+0,3	00,16	0,09	0+0,12
6	6,1	3,7	+1,4	–0,1	01,96	0,01	0–0,14
7	2,7	2,6	–2,0	–1,2	04,00	1,44	0+2,40
8	4,9	4,4	+0,2	+0,6	00,04	0,36	0+0,12
9	3,1	2,0	–1,6	–1,8	02,56	3,24	0+2,88
10	3,7	4,5	–1,0	+0,7	01,00	0,49	0–0,70
	47,3	37,9	+0,3	-0,1	30,37	15,93	+18,64

2.Вычисление  по формуле (2.28), которая в данной задаче примет вид: 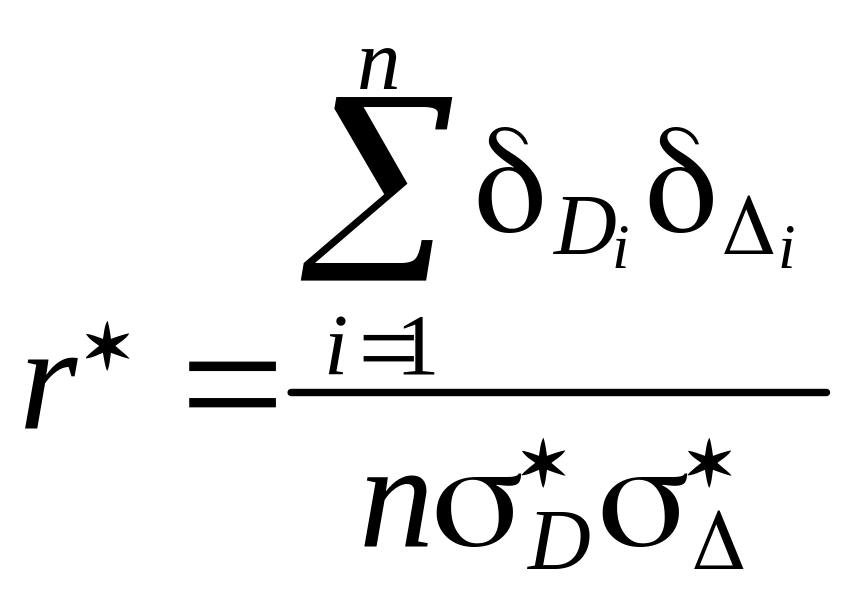; (2.34)

; ; .

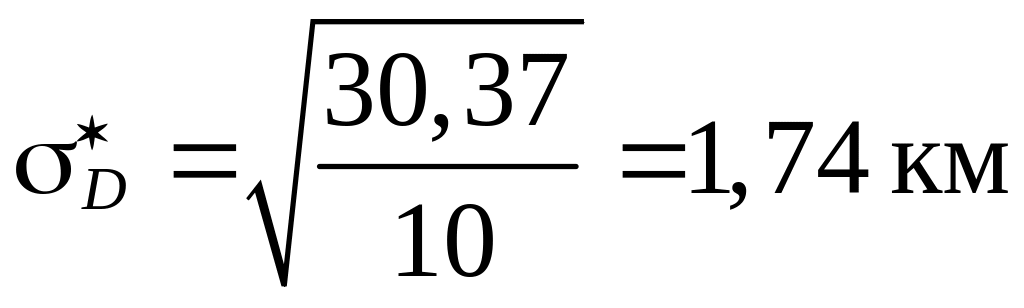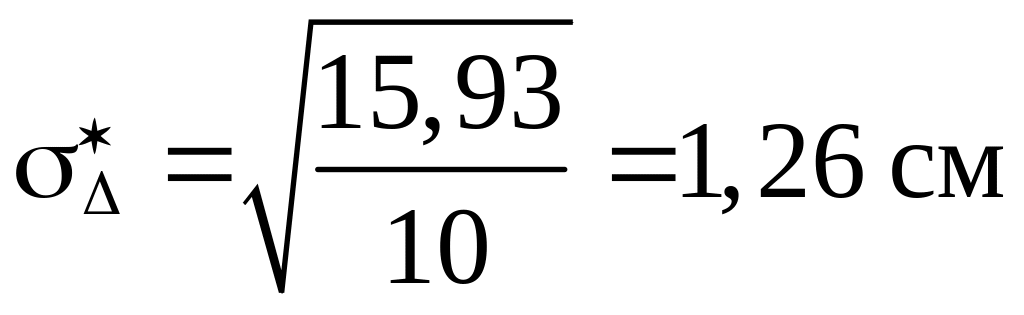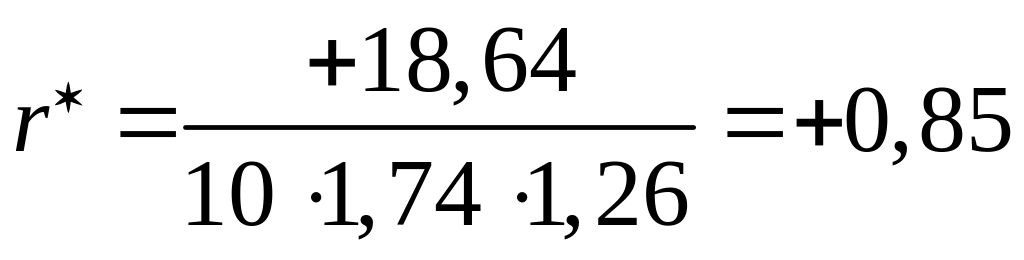3. Оценка надёжности  .

Так как число измерений небольшое ( ), то для оценки надёжности применим критерий Фишера. Этот критерий основан на преобразовании вида:

.

(2.35)

Величина  подчинена нормальному закону распределения с параметрами М( )=Z и ². По таблице Приложения C, пользуясь коэффициентом корреляции  , как аргументом, находим . Доверительный интервал для истинного значения  Z имеет вид:

.

(2.36)

определяем по формуле

.

(2.37)

Для вероятности 0,90 по таблице Приложения B находим коэффициент и определяем границы доверительного интервала для Z :

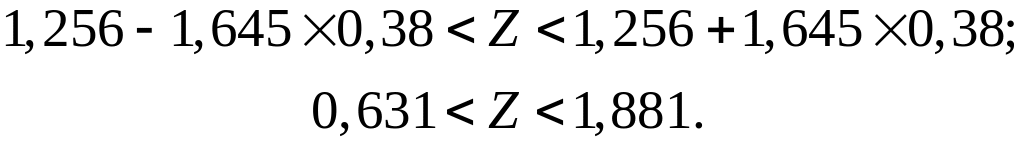
Затем из таблицы Приложения C находим соответствующие крайним значениям Z  значения границ коэффициента корреляции (0,56 и 0,95). Получаем доверительный интервал, с вероятностью 0,90 накрывающий истинное значение коэффициента корреляции r:

.

Так как имеет место соотношение:

; ( ), то прямолинейную корреляционную связь между величинами D и   можно считать установленной.

4. Составим уравнение регрессии  на D: ,

приведём его к виду: , где ;

.

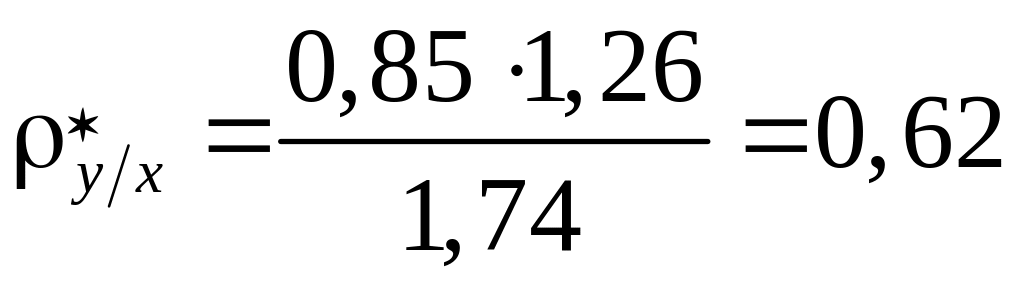Получаем окончательно уравнение регрессии  на D

.

(2.38)

Затем по уравнению (2.38) строим на графике рис. 2.2 прямую линию.

Достоинство уравнения регрессии (2.38) состоит в том, что оно позволит по заданным значениям переменной D (в км) предвычислять ожидаемые в среднем значения переменной  (в см).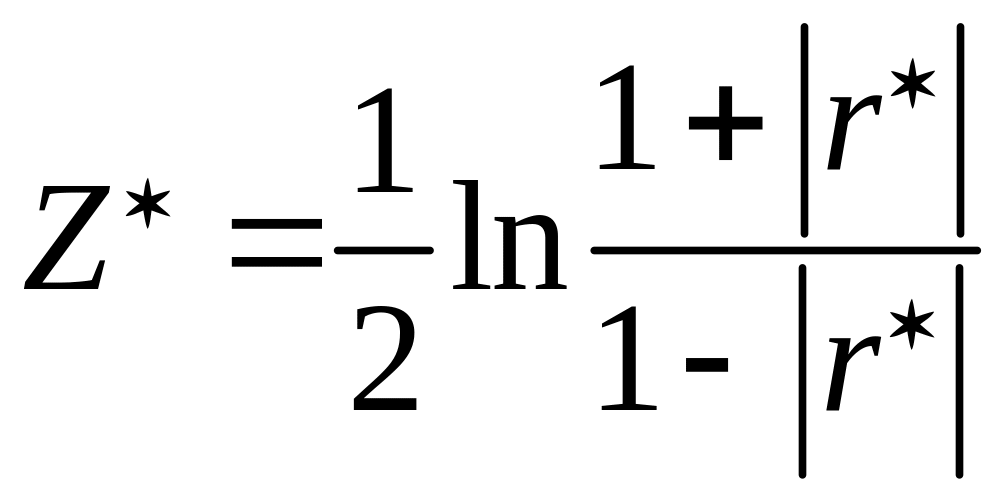