МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

"Московский технологический университет"

МИРЭА

Институт Кибернетики

Кафедра БК-252

Реферат

по дисциплине

«Псевдослучайные последовательности»

Тема курсового проекта:

«Генератор случайных чисел на основе преобразований Лоренца.»

Студент группы ККСО-02-12: Витин Я.В.

Руководитель курсового проекта: к. ф-м. н., п. Зязин В.П.

Рецензент:

Работа представлена к защите: «___» _________________________ 2016 г.

Допущен к защите: «___» _________________________ 2016 г.

Москва, 2016 г.

ВВЕДЕНИЕ

В последние годы хаос притягивал интересы многих исследователей в областях физики, математики, вычислительной техники. Кроме того, хаос привлекал внимание широких масс, и словосочетание «точка бифуркации» стало широко распространенным в статьях чаще, чем прежде. Теория хаоса используется учеными для объяснения и прогноза поведения систем в реальном слове. На самом деле, известные функции хаотических систем, такие как, сильная зависимость от начальных условий, топологической транзитивности, широкого расширенного спектра ее сигнала, и т.д., непосредственно наталкивают на идею использовать подходящие генераторы хаоса, чтобы создать новое поколение методов надежного шифрования (Кокарев и др. (1992); Куомо и др. (1993); Ян и др. (1997); Целиковский и др. (2006); Линник и Целиковский (2010); Баптиста (1998)).

В современной жизни много людей используют кредитные карты для покупок, социальные сети для связи, интернет-банкинг для того, чтобы оплатить счета, интернет-телефон и коммуникации, службы коротких сообщений (SMS) и т.д. Обычно все это действие защищено методами надежного шифрования.

В классической криптографии есть два вида схем шифрования, основанных на различных ключевых методах распределения. Один из них - симметричная криптографическая система (криптографическая система секретного ключа), которые используют те же самые криптографические ключи и для шифрования простого текста и для дешифрования шифрованного текста. Симметричные криптографические системы могут использовать или поточные шифры или блочные шифры Мао (2004). Для распределения безопасных ключей в симметричных криптографических системах используются встреча с глазу на глаз, курьер, которому доверяют или существующий канал надежного шифрования. Первые два перечисленных метода не очень реалистические и часто непрактичны, в то время как третий метод зависит от безопасности предыдущего ключевого обмена. Для ключевого обмена может использоваться метод Диффи Хеллмена (1976). Ключевой обмен Диффи Хеллмена - определенный метод безопасного обмена криптографическими ключами по каналу общего доступа, и это - первый определенный пример асимметричной криптографической системы (с открытым ключом). Второй вид криптографических систем, который использует два отдельных ключа, один из которых секретный и один из которых общедоступен. Для поколения сочетания ключей в симметричных и асимметричных

криптографических системах используются генератор случайных чисел (RNG) или генератор псевдослучайных чисел (PRNG). В вычислении RNG вызывают аппаратным истинным генератором случайных чисел (TRNG). TRNG - аппарат, который генерирует случайные числа используя физический процесс, а не просто компьютерную программу. Такие устройства часто основаны на микроскопических явлениях, которые производят низкий уровень, статистически случайные «шумовые» сигналы, такие как тепловой шум, фотоэлектрический эффект и другой, квантовые LLC явления (2010). Кроме того, качество камер, встроенных в мобильные телефоны, улучшилось так, чтобы теперь они стали чувствительны к небольшому уровню света. Сангуйнетти и др. (2014) демонстрирует, как эти свойства могут использоваться, чтобы произвести случайные числа квантового источника.

RNG может использоваться для генерации истинных случайных чисел (основа), которое используется в PRNG для генерации псевдослучайных чисел. Любая криптографическая система с супералгоритмом устойчивого шифрования может быть повреждена, если это использует плохой ключевой алгоритм выбора. Поэтому, корпорация Intel объединила TRNG который прежде всего демонстрационный тепловой шум, усилив напряжение, измеренное через неуправляемые резисторы в Концентраторе Встроенного микропрограммного обеспечения Intel 82802 в 1999. Впоследствии, у этого TRNG есть проблема с увеличенной потребляемой мощностью, скоростью генерации случайных чисел и совместимостью с производственным процессом (связанным с сокращением размера транзисторов в процессорах). Позже, Digital Random Number Generator (DRNG), описанный в Srini-vasan и др. (2009, 2010) и интегрированный в семье процессоров Ivo Bridge, был создан для корпорации Intel. Кроме того, TRNG интегрирован в процессорах VIA C3 company Cryptography Research (2003).

В работе Оиши и Иноуэе (1982) исследователи разработали первое основанное PRNG на хаотической системе. Прошлые два десятилетия, PRNG, основанный на хаотических системах, был фокусом исследования для многих исследователей: (Фридрич (1998); Квок и Тан (2007); Леи и др. (2006); Литий и др. (2005); Стояновский и Кокарев (2001); Ялчин и др. (2004); Нянь-Шэн (2011)). В Чене и др. (2001), основанными RNG на схеме Chua являются аппаратные реализации. Ху и др. (2013) предложил основанное PRNG на Ченовских хаотических системах. Позже, Оскайняк и Явук (2013) показал, что произведенные псевдослучайные последовательности числа были получены при помощи атаки грубой силой уменьшенного ключевого пространства. В этой статье два генератора псевдослучайного числа получены при помощи обобщенной системы Лоренца (GLS). Один из PRNG основан на сумме трех координат хаотических орбит GLS. Другой основан на комбинации трех координат хаотических орбит GLS. Статистические тесты и анализ безопасности показывают, что у предложенного алгоритма есть полезные псевдослучайные особенности, высокая чувствительность к изменению ключа и защита против атаки. Остальная часть статьи содержит следующее. В Разделе 2, кратко повторяются некоторые известные факты об обобщенной системе Лоренца. В разделе 3, введены алгоритмы PRNG для обобщенной системы Лоренца, которые проанализированы в Разделе 4. Заключительный раздел дает некоторые заключения и перспективы будущего исследования.

1. Обобщенная система лоренца

Во-первых, давайте вспомним некоторые ранее опубликованные результаты на обобщенной классификации систем Лоренца. Более подробная информация может быть найдена в работах Целиковского и Чена (2002, 2005). Следующую общую нелинейную систему обыкновенных дифференциальных уравнений в R³ вызывают обобщенной системой Лоренца (GLS):

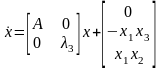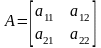, (1),

где x = [x₁;x₂;x₃]^T, и A имеет собственные значения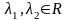 , такой что – ­­−λ₂ > λ₁ > − λ₃ > 0. (2)

Неравенство (2) обращается к анализу хаоса, известного как хаоса Шильникова, и может быть рассмотрено, как необходимое условие для существования хаоса, см. более детальное обсуждение в работе Целиковского и Чена (2002). GLS, как говорят, нетривиален, если у него есть по крайней мере одно решение, которое не уходит ни в ноль, ни в бесконечность, ни к циклу. Следующий результат, включая эффективный синтез богатого разнообразия хаотических поведений для GLS, был получен Целиковским и Ченом (2002): Для нетривиальной обобщенной системы Лоренца (1) - (2), существует неисключительная линейная смена системы координат, z = Tx, которая приводит (1) в следующую обобщенную каноническую форму Лоренца:

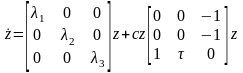(3),

где z = [z₁;z₂;z₃]^T, с = [1;-1;0]^T и параметр .

Фактически, параметр τ играет важную роль единственного скалярного параметра бифуркации, в то время как остальные параметры имеют только качественное влияние, являющееся собственными значениями при линеаризации GLS в источнике. Эти качественные параметры просто требуются, чтобы удовлетворять устойчивому условию (2), так, чтобы точная настройка могла быть сделана, используя только единственный скалярный параметр τ. Таким способом диапазон параметра, который будет использоваться в PRNG позже, далее расширяется. В работе Целиковского и Чена (2005) дана полная и хорошая классификация всех связанных систем, показав, что многие недавно представленные в литературных классах являются фактически особыми случаями GLS.

Рис. 1. Аттрактор обобщенной системы Лоренца с

параметрами λ₁ = 8, λ₂ = −16, λ₃ = −1, τ= 0.1.

2. Описание алгоритмов prng

Предложенные PRNG основаны на временном ряде, полученном от обобщенных хаотических систем Лоренца, от их канонической формы, описанной уравнением (3). В работе предложены и проанализированные два различных алгоритма для генерации псевдослучайной двоичной последовательности, основанной на GLS. Сначала они определяются следующими уравнениями:

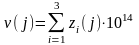(4)

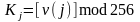(5)

где , j = 0, 1, 2... N и z₁ (i), z₂ (i), z₃ (i) выборки обобщенной системы Лоренца.

Операция [·] самая близкая функция целого числа P754 (2008), известная как круглая функция. Очень похожий алгоритм PRNG, используемого в работе Гарсии и др. (2013). Алгоритм PRNG, основанный на (4) и (5), выполняется следующим образом (см. также Рис 2):

(1) ключ, которые состоят из начального условия z₁ (0), z₂ (0), z₃ (0), выбран при помощи TRNG.

(2) трехмерная последовательность z₁ (i), z₂ (i), z₃ (i) произведена, выбрав хаотическую орбиту, обобщают системную каноническую форму Лоренца (3).

(3) одномерная последовательность получается при помощи формул (4) и (5).

(4), последовательность K_j преобразовывается в двоичную последовательность с длиной блока на 8 битов (т.е. 0 преобразовывается в 00000000, и 255 преобразовывается в 11111111).

Рис. 2. Схема PRNG, основанного на обобщенном

хаотической системы Лоренца.

Другая модификация алгоритма PRNG, которая основана на GLS, используемом на основании следующих уравнений

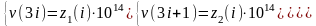(6)

(7),

где , i = 0, 1, 2... N, j = 0, 1, 2... 3N+2 и z₁ (i), z₂ (i), z₃ (i) получены от обобщенных хаотических систем Лоренца, от их канонической формы (3). Этот алгоритм PRNG выполняется следующим образом (см. также Рис 3):

(1) ключ, которые состоят из начального условия z₁(0), z₂(0), z₃(0), выбран при помощи TRNG.

(2) трехмерная последовательность z₁(i), z₂(i), z₃(i) произведена, выбрав хаотическую орбиту обобщать системной канонической формы Лоренца (3).

(3) Одномерная последовательность получена с использованием формул (6) и (7).

(4), K_j преобразовывается в двоичную последовательность с длиной блока на 8 битов (т.е. 0 преобразовывается в 00000000, и 255 преобразовывается в 11111111).

Алгоритм, используя (6) и (7) производит трижды повторенное количество псевдослучайных чисел по сравнению с алгоритмом, используя (4) и (5). Оба из алгоритмов используют комбинацию трех координат хаотическая орбита. Не рекомендуется использовать первые 100 псевдослучайных чисел, произведенных PRNG из-за переходного состояния хаотической системы.

Рис. 3. Схема основанного PRNG на обобщенном Лоренце хаотическая система.