0

Томский межвузовский центр дистанционного образования

Томский государственный университет систем управления и радиоэлектроники (ТУСУР)

Кафедра компьютерных систем в управлении и проектировании (КСУП)

Контрольная работа № 2

по дисциплине «Теория вероятностей и математическая статистика»

(Учебное пособие «Математика IY. Основы теории вероятностей и математическая статистика» З. А. Смыслова Томск - 2000)

Тема: Контрольная работа № 2

Вариант 4

Задача 1. Тема: «Нормальное распределение»

Вариант 4

Средний срок службы коробки передач до капитального ремонта у автомобиля определенной марки составляет 56 мес. со стандартным отклонением Привлекая покупателей, производитель хочет дать гарантию на этот узел, обещая сделать бесплатно любое число ремонтов коробки передач нового автомобиля в случае ее поломки до определенного срока. Пусть срок службы коробки передач подчиняется нормальному закону. На сколько месяцев в таком случае производитель должен дать гарантию для этой детали, чтобы число бесплатных ремонтов не превышало 2.275 % проданных автомобилей?

РЕШЕНИЕ

Срок службы должен оказаться в интервале а=56 мес., мес, .

Применим формулу:

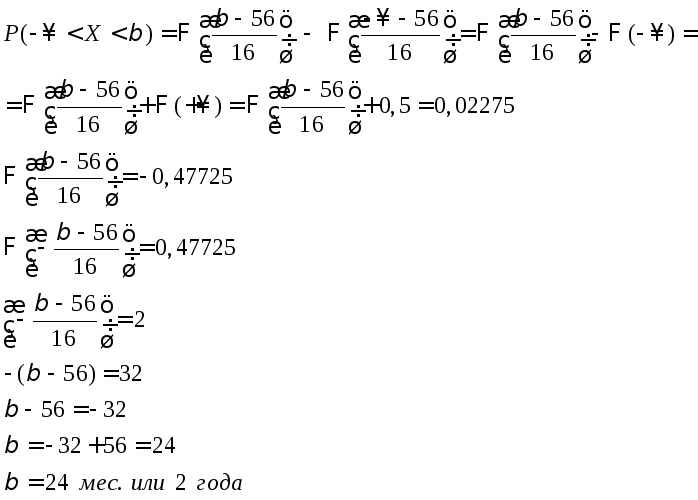
Чтобы число бесплатных ремонтов не превышало 2,275% проданных автомобилей, производитель в данном случае должен дать гарантию для этой детали на 2 года.

Задача 2.Тема: «Критические точки» (работа с таблицами)

По заданной вероятности (и заданному числу степеней свободы k) найти критическую точку (квантиль ), пользуясь соответствующими таблицами (приложение 1–4):

а) стандартного нормального распределения;

б) распределения «хи-квадрат»;

в) распределения Стьюдента;

г) распределения Фишера.

Нарисовать примерный вид графика плотности распределения, указать критическую точку, заштриховать площадь, соответствующую вероятности , записать пояснения к рисунку.

Вариант 4: а) γ = 0.97; б) γ = 0.95, k = 6; в) γ = 0.95, k = 8; г) γ = 0.99, .

РЕШЕНИЕ

а) γ = 0,97. Найти критическую точку стандартного нормального распределения.

.

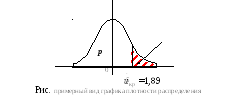
Критическая точка является границей, правее которой лежит 3% площади под кривой плотности стандартного нормального распределения. Значит площадь под этой кривой на интервалесоставляет 47% и в таблице значений функции Лапласа (приложение 1) ищем значениеЭто значение достигается прит.е. критическая точка.

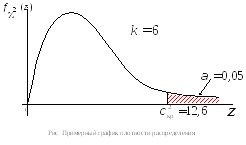
б) γ = 0.95, k = 6; найти критическую точку распределения «хи-квадрат»;

Для случайной величины вероятностьПо таблице критических точек распределения «хи-квадрат» (приложение 2) находимЗначит вероятность этой случайной величинеK принять значение, большее 12,6, - меньше 0,05.

в) γ = 0.95, k = 8. Найти критическую точку распределения Стьюдента.

Для случайной величины Х, распределенной по закону Стьюдента с степенями свободы принаходим по таблице (приложение 3) одностороннюю критическую точкуЭто означает, что при испытаниях вероятность наблюдать значение этой случайной величины, большееменьшее

т.е. площадь под кривой плотности распределения, лежащая правее критической точки, составляет от всей площади.

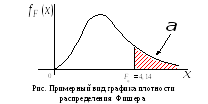
г) γ = 0.99, . Найти критическую точку распределения Фишера.

и Критическая точкат.е. вероятность получить значениеХ, большее 4,14, меньше 0,01. В среднем в 99 случаях из 100 будем наблюдать значения, меньшие 4,14.

Задача 3. Тема: «Интервальные оценки»