Вариант 4

Основные фонды 30 предприятий, млн руб.:

4.2	2.4	4.9	6.7	4.5	2.7	3.9	2.1	5.8	4.0
2.8	7.3	4.4	6.6	2.0	6.2	7.0	8.1	0.7	6.8
9.4	7.6	6.3	8.8	6.5	1.4	4.6	2.0	7.2	9.1

Решение

а) найти выборочные значения среднего арифметического, моды, медианы;

1	4,2
2	2,4
3	4,9
4	6,7
5	4,5
6	2,7
7	3,9
8	2,1
9	5,8
10	4
11	2,8
12	7,3
13	4,4
14	6,6
15	2
16	6,2
17	7
18	8,1
19	0,7
20	6,8
21	9,4
22	7,6
23	6,3
24	8,8
25	6,5
26	1,4
27	4,6
28	2
29	7,2
30	9,1

Среднее арифметическое обозначается и Для несгруппированных данных среднее арифметическое определяется по следующей формуле:

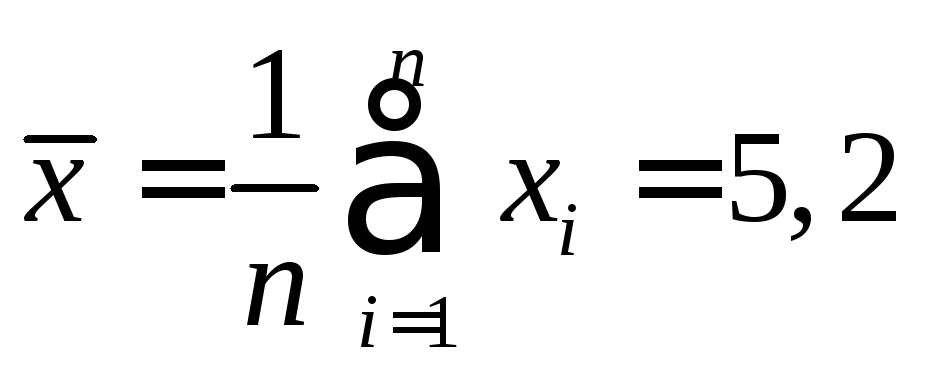
где n — объем выборки; х_i — варианты выборки.

Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

      Ряд называется унимодальным, если в нем только одно модальное значение и полимодальным, если есть несколько значений признака, которые встречаются одинаково часто. Для полимодального ряда, каким является наш ряд, моду не вычисляют.

Для определения медианы необходимо представить ряд в виде упорядоченной последовательности значений:

0,7

1,4

2

2

2,1

2,4

2,7

2,8

3,9

4

4,2

4,4

4,5

4,6

4,9

5,8

6,2

6,3

6,5

6,6

6,7

6,8

7

7,2

7,3

7,6

8,1

8,8

9,1

9,4

Медиана – величина признака, которая делит упорядоченную последовательность значений на две равные по численности части.

Медианой (Ме) называется такое значение признака X, когда ровно половина значений экспериментальных данных меньше ее, а вторая половина — больше.

     Если данных немного (объем выборки невелик), медиана вычисляется очень просто. Для этого выборку ранжируют, т. е. располагают данные в порядке возрастания или убывания, и в ранжированной выборке, содержащей n членов, ранг R (порядковый номер) медианы определяется как

   

и медиана совпадает с числом, порядковый номер которого равен рангу.

Но, если выборка содержит четное число членов, как в нашем случае, то медиана не может быть определена столь однозначно.

      Ранг медианы оказывается равным

     

Медианой в этом случае может быть любое число между 4,9 и 5,8 (15-м и 16-м членами ряда). Для определенности принято считать в качестве медианы среднее арифметическое этих значений, т. е.

д) построить сгруппированный статистический ряд и гистограмму;

Если значения изучаемого признака могут отличаться друг от друга на сколь угодно малую величину (непрерывная генеральная совокупность) или объем выборки велик, то данные представляют в виде сгруппированного статистического ряда. Для этого весь диапазон значений вариант разбивают на 5–12 интервалов необязательно одинаковой длины и подсчитывают число вариант, попавших в каждый интервал (частотуi-го интервала). Полученные данные заносятся в таблицу, которая называется интервальной таблицей частот или сгруппированным статистическим рядом.

Рекомендуемое количество интервалов рассчитывают по эмпирической формуле Старджеса

где n — объем выборки. Длину i-го интервала принимают равной

где —наибольшее, а— наименьшее значение в вариационном ряду.

Сгруппируем эту выборку. наименьшие основные фонды равны 0,7 млн. руб, наибольшие – 9,4 млн. руб.

По формуле Старджеса k=5,875;

.

Упакуем выборку в интервал [0,7;9,7], который разобьем на 6 частей длиной d=1,5

Подсчитаем частоту (относительную частоту) для каждого интервала и получим сгруппированный статистический ряд.

Сгруппированный статистический ряд

Интервалы					[0,7;2,2)					[2,2;3,7)						[3,7;5,2)					[5,2;6,7)					[6,7;8,2)					[8,2;9,7)
Частоты					5					3						7					5					7					3
Относительные частоты					0,167					0,1						0,233					0,167					0,233					0,1
0,7	1,4	2	2	2,1		2,4	2,7	2,8	3,9		4	4,2	4,4	4,5	4,6		4,9	5,8	6,2	6,3		6,5	6,6	6,7	6,8		7	7,2	7,3	7,6		8,1	8,8	9,1	9,4

Наглядно сгруппированный статистический ряд представляют в виде гистограммы. Гистограмма — это фигура, составленная из прямоугольников, основаниями которых служат интервалы группировки. Высота i-го прямоугольника определяется по формуле

где d — длина i-го интервала. Таким образом, высота каждого прямоугольника пропорциональна частоте попадания в данный интервал, а сумма высот равна

Гистограмма позволяет оценить вид графика плотности распределения непрерывной случайной величины

е) найти модальный и медианный интервалы, сравнить середины этих интервалов со значениями моды и медианы, рассчитанными по выборке.

Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

      Ряд называется унимодальным, если в нем только одно модальное значение и полимодальным, если есть несколько значений признака, которые встречаются одинаково часто. Для полимодального ряда моду не вычисляют.

      Для дискретного ряда мода находится по определению.

      Интервал группировки с наибольшей частотой называется модальным.

В математической статистике мода определяется по выборке, как варианта с наибольшей частотой.

Если выборка сгруппирована, то сначала определяют модальный интервал, т.е. интервал с наибольшей частотой. В качестве моды можно взять середину модального интервала [3,7;5,2) – 4,45 или[6,7;8,2) – 7,45. При этом среднее значение двух этих значений равно 5,95.

В теории вероятностей медианой непрерывной случайной величины Х называется такое число чтоСоответственно, по выборке находят приближенное значение медианы — числотакое, что половина вариант выборки меньше этого числа, а половина — больше него.

Работая со сгруппированной выборкой, вначале находят медианный интервал такой, что относительная накопленная частота дляменьше 0.5, а для— больше 0.5. В нашей задаче таким интервалом является интервал[5,2;6,7) В качестве медианы можно взять середину этого интервала:Это больше чем выборочное значение медианы, которое, как было посчитано, равно 5,35.

г) найти верхнюю и нижнюю выборочные квартили, пояснить их смысл;

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше. Можно найти три числа которые аналогичным образом делят выборку на четыре равные части. Эти числа называются квартилями. Числосовпадает с медианой,называется нижней, а— верхней квартилью. В теории вероятностей квартилями непрерывной случайной величиныХ называются значения определяемые из условия:

Таблица накопленных частот

Интервалы					[0,7;2,2)					[2,2;3,7)						[3,7;5,2)					[5,2;6,7)					[6,7;8,2)					[8,2;9,7)
Накопленные частоты					5					8						15					20					27					30
Относительные накопленные частоты					0,167					0,267						0,5					0,67					0,9					1
0,7	1,4	2	2	2,1		2,4	2,7	2,8	3,9		4	4,2	4,4	4,5	4,6		4,9	5,8	6,2	6,3		6,5	6,6	6,7	6,8		7	7,2	7,3	7,6		8,1	8,8	9,1	9,4

Накопленной частотой называется число вариант выборки, меньших данного числах. Для сгруппированного статистического ряда определяется— число вариант, меньших правой границыi-го интервала. Относительная накопленная частота — это отношение накопленной частотык объему выборкиn.

б) найти размах выборки, выборочную дисперсию, выборочное среднее квадратическое отклонение; проверить выполнение правила «3сигма»;

Размах выборки равен разности максимальной и минимальной вариант.R = 9,4-0,7 = 8,7.

Выборочная дисперсия

Корень квадратный из выборочной дисперсии называется выборочным средним квадратическим отклонением (с.к.о.).

=2,4, т. е. в среднем основные фонды предприятия отличаются от среднего значения основных фондов на 2,4 млн. рублей.

В теории вероятностей для нормального закона распределения доказывается правило «трех сигма»:

Это правило приблизительно выполняется для большинства унимодальных законов распределения и для выборок из таких генеральных совокупностей: более 99 % выборочных значений лежат в интервале . Аналогично для «двух сигма»: более 95 % выборочных значений лежат в интервалеДля нашей выборки имеем

,

и 100 % выборочных значений лежат в этом интервале.

в) оценить симметричность распределения с помощью первого коэффициента Пирсона;

первый коэффициент асимметрии Пирсона:

.

Для выборки примера 2 значение этого коэффициента

отлично от нуля, т.е. можно принять, что наша выборка извлечена из генеральной совокупности с асимметричным законом распределения, асимметрия будет отрицательной.

Те же расчеты можно выполнить при помощи таблицы.

Замечание. Если исходный вариационный ряд недоступен, приведенные выше формулы вычисления выборочных характеристик, применимые только к дискретному ряду, могут быть использованы дляприближенноговычисления выборочных характеристик непрерывного признака, представленного интервальным рядом. Для этого предварительно каждый интервалxi–1–xiзаменяется его серединой= (xi–1+ xi) / 2, то есть производится замена интервального ряда дискретным, соответствующим ему приближенно.
Основные фонды предприятий (Х, млн.руб.): xi–1–xi	Число предприятий(mi)		mi	Н()		()2 mi
[0,7;2,2)	5	1,45	7,25	5	70,31	10,51
[2,2;3,7)	3	2,95	8,85	8	15,19	26,11
[3,7;5,2)	7	4,45	31,15	15	3,93	138,62
[5,2;6,7)	5	5,95	29,75	20	2,81	177,01
[6,7;8,2)	7	7,45	52,15	27	35,44	388,52
[8,2;9,7)	3	8,95	26,85	30	42,19	240,31
Итого	30	-	156	-	169,875	981,075

Легко убедиться, что в случае дискретного признака Хв ранжированном вариационном рядуx_j =приН() + 1j Н(). Для рассматриваемого примера: x_j = 4,45 при 16 j 20.

Объем выборки n = 30 – число четное. Пустьn= 2j, тогдаj = 15. Поэтому:

Частота достигает максимума: m_i = m_max = 7 при x_i = 4,45 и x_i = 7,45, поэтому:

х_мо = 4,45 и 7,45 (млн. руб.).

Очевидно х_мo х_ме– распределение асимметричное.

R = х_max – х_min =9,4 – 0,7 =8,7

Дисперсию рассчитываем двумя способами.

1) ;

2) ;

= 32,70 – (5,2)² = 5,66.

 2,38 (млн. руб.), то есть основные фонды предприятия отклоняются от средних фондов предприятий в среднем на 2,38 (млн. руб.)